The Construction of Drawings and Movies

Models for Architectural Design and Analysis

Thomas Forget

• Editorial: Routledge
• Año: 2012
• ISBN:
  9781136229831
• Edición: 1
• Categoría: Arquitectura
• Categoría: Diseño arquitectónico

The architectural imagery that you create is most effective when it examines your project in an abstract manner. Most students and practitioners understand linear perspective and cinema to be examples of architectural presentation tools. This book asks you to consider drawings and movies to be analytical tools that give you the capacity to engage all phases of the design process, from parti to presentation.

The ways in which spaces relate to each other and how materials connect to each other in your projects are as important as your building's appearance. As digital tools increasingly allow you to simulate the experience of built and unbuilt environments, it is essential that you scrutinize the nature of architectural imagery and resist the lure of virtual reality. Though pure simulation may be appropriate for your clients, your design process requires abstraction and analysis.

Author Thomas Forget demonstrates how to construct analytical drawings and movies that challenge the alleged realism of linear perspective and cinema. These demonstrations expose you to underlying principles that will allow you to understand the broader implications of these methods. In addition, historical surveys of drawings and movies provide you with insight into how architects and architectural historians have understood the role of linear perspective and cinema in their fields. Finally, examples of drawing and moviemaking strategies illustrate how you can apply the lessons of the book to precedent analyses and design projects.

Part I—Construction Logic

Chapter 1

The Demystification of Linear Perspective

An object reflects a pattern of light on to the eye. The light enters the eye through the pupil, is gathered by the lens, and thrown on the screen at the back of the eye, the retina. On the retina is a network of nerve fibers which pass the light through a system of cells to several millions of receptors, the cones. The cones are sensitive both to light and to colour, and they respond by carrying information about light and colour to the brain. It is at this point that human equipment for visual perception ceases to be uniform, from one man to the next.

Michael Baxandal, Painting and Experience in Fifteenth-Century Italy

The history of linear perspective is a complicated web of empirical discoveries and geometric proofs. It has two distinct identities, one as a practical tool in the service of image-making, and one as a theoretical discipline of mathematics. While many practitioners are unaware of the theoretical underpinnings of their tool, many theoreticians are unversed in the practical implications of their inquiries. In general, artists and architects execute methods, in varying degrees of correctness, that they do not understand, and mathematicians prove the correctness of methods that they do not execute. Significant exceptions exist—such as Piero della Francesca, whose fifteenth-century treatise on linear perspective makes significant contributions to both practice and theory—but artistic and scientific approaches to linear perspective usually do not overlap. Since the early twentieth century, overlap has been virtually non-existent because both art and science have increasingly disregarded the contemporary relevance of linear perspective. While some artists and architects regard the scientific nature of linear perspective as an oppressive obstacle to subjectivity, some mathematicians question its scientific significance in light of more complex understandings of geometry. To some, linear perspective is simply a matter of history that inspires wonderment and adoration, as well as confusion and disrespect. It is an enigmatic and, to some degree, nomadic specialty. Throughout this book, I refer to linear perspective as a drawing system (as opposed to a field or discipline) because it belongs to no one category of thought. Like architecture itself, it is both art and science, or perhaps neither. This book seeks not only to revive linear perspective as a relevant drawing practice, but also to blur the distinction between its artistic and its mathematical identities. In the context of architectural analysis and design, practice and theory must be integral to each other.

Most treatises on linear perspective since Alberti’s begin with an arrogant (and usually correct) assumption that previous treatises fail to clearly and adequately describe the drawing system.¹ In 1754, for example, Joshua Kirby published an English language treatise whose title exemplifies this propensity: Dr. Brook Taylor’s Method of Perspective Made Easy, Both in Theory and Practice. In Two Books. Being An Attempt to make the Art of Perspective easy and familiar; To Adapt it intirely to the Arts of Design; And To make it an entertaining Study to any Gentleman who shall chuse so polite an Amusement. In short, Kirby aims to correct the pedagogical shortcomings of his predecessor and to clarify the relevance of the drawing system to a specific audience. Variations of the phrase “perspective made easy” appear in treatise titles throughout history and as recently as 1999. The assumption behind this tendency is that the drawing system is inherently difficult to understand and that a specific method unlocks the mystery. My explanation of linear perspective disputes these implications, even as I proclaim (exactly like my predecessors) to improve upon previous efforts to explicate the drawing system. My approach is to assume that linear perspective is a perfectly simple geometric system and that an understanding of a few basic properties allows for an effortless navigation through the entire system. What follows is neither a mathematical theory nor a practical method, but rather a construction logic that demystifies linear perspective and emphasizes inherent geometric relationships between linear perspective and orthographic drawing. Although the demonstration of my construction logic resembles a step-by-step procedure, the objective is to instill a deep comprehension of the drawing system that eliminates the necessity to memorize the given steps, or even to follow them. The theoretical explanation that follows the demonstration delves into mathematical properties more than most practical treatises, but it does not include the type of geometric proofs that accompany most theoretical treatises. It will therefore please neither the practitioner, who simply wants to make a picture, nor the mathematician, who expects complete geometric substantiation. Like Kirby, I seek to articulate the significance of the drawing system to a specific audience, which in my case consists of architects and architecture students, who are particularly qualified to understand the reciprocity between linear perspective and orthographic drawing.

The Geometric System

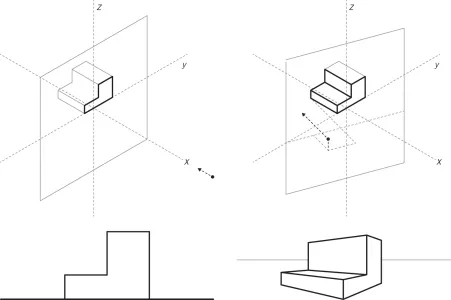
Euclidean geometry is a spatial system that is defined by three orthogonally orientated axes, commonly referred to as the x-axis, y-axis, and z-axis. Both orthographic drawing and linear perspective are modes of projection that provide views of a Euclidean spatial system (see Figure 1.1). The point of projection (or view point) in an orthographic view is located infinitely distant from and, by implication, somehow outside of the spatial system.² The point of projection in a linear perspective, by contrast, is located inside the spatial system. In both orthographic and perspectival projection, the point of projection may be located at an infinite number of locations, each of which provides a unique view of the given object of projection. In an orthographic projection, the location of the point of projection does not have proper coordinates because it lies at infinity. In a perspectival projection, the location of the point of projection is literally a Euclidean point with three coordinates (x, y, z). The projection itself, however, is non-Euclidean, as it violates one of the fundamental principles of Euclidean geometry: whereas parallel lines never converge in Euclidian geometry, parallel lines always converge in linear perspective. A linear perspective, therefore, may be understood as a non-Euclidean projection of a Euclidean space.

Figure 1.1: orthographic (left) and perspectival (right) projection

Linear perspective is typically understood as a subjective mode of projection, and orthographic drawing is typically understood as an objective mode of projection. Whereas the former is assumed to be phenomenological, the latter is assumed to be cognitive. This book challenges these assumptions and contends that the relationship between perspectival and orthographic projection is reciprocal, not exclusive. The point of view in a linear perspective may be drawn in plan, section, elevation, and axonometric. Likewise, orthographic drawings are embedded within a linear perspective and may be extracted from it. In Euclidean spatial systems, projective drawing promotes exchanges between interior (perspectival) and exterior (orthographic) points of view, as each type may be used to construct the other. To draw in linear perspective is to draw in plan and in elevation at the same time.

The beauty of this reciprocity eludes even most architects and architecture students, despite their familiarity with both modes of projection. This is because conventional explanations of linear perspective involve opaque and overly complex methods of construction that obscure the fundamental (and rather simple) geometric laws that underlie the drawing system. In this chapter, I remove the veil of mystery and lay bare the principles that underlie the drawing system. Chapter 3 further explores how a multitude of linear perspective construction methods all obey the same principles. The apparent differences lie in the ways in which the drawing system in entered and the ways through which it is navigated. There is, however, only one system, and a thorough understanding of the quasi-Euclidean nature of linear perspective eliminates the need to memorize any particular method.

Definitions and Parameters

Throughout this book, I will use specific terms to refer to various components and properties of linear perspective, and it is important to clarify the precise meaning of my usage of these terms. Many of the terms are common to other methods and explanations of the drawing system, but some of them are used in a way that diverges from common usage. Still others are unique to this book. Readers may find it useful to refer to the diagrams and drawings on pages 28–31 while they review the definitions. The diagrams illustrate the definitions in isometric projections in order to better communicate the relative locations of the components of the drawing system. It is important to note that the definitions apply only to linear perspectives in which the primary angle of viewing is parallel to the ground plane. This is the most commonly executed type, and the demonstration of the construction logic is an example of it; however, I include the phrase, “in the most basic orientation of linear perspective,” repeatedly in this chapter in order to emphasize that there are other ways to operate the drawing system. At the end of this chapter, several construction variables will be considered, some of which, like perspectival projections in which the primary angle of viewing intersects the ground plane, adhere to slightly modified definitions. These more complex constructions may require more time and concentration than a basic construction, but no variable is too complex to address once the basic principles of linear perspective are understood. In all cases, the construction logic never varies because the mathematical laws never change.

The ground plane (in the most basic orientation of linear perspective) is a plane that is defined by the x-axis and the y-axis. Its position is determined arbitrarily, and this position sets the zero-value of the z-axis. Points above the ground plane have positive z-values, and points below it have negative z-values.

The measuring plane (in the most basic orientation of linear perspective) is a plane that is defined by the x-axis and the z-axis, so it is perpendicular to the ground plane. Its position is determined arbitrarily, and this position sets the zero-value of the y-axis. Points in front of the measuring plane have negative y-values, and points behind it have positive y-values. Its front and back are determined by the location of the viewing point (see below). In other methods, the measuring plane is known as the picture plane. Measuring plane is a more useful term because it emphasizes the fact that it is the only plane in a perspectival projection in which dimensions may be measured to scale. The term also deemphasizes the pictorial assumptions of linear perspective. The measuring plane is not a one-way window onto a scene, and objects on both sides of it may appear on it.

A measuring point is a point that lies on the measuring plane.

The ground line (in the most basic orientation of linear perspective) is the intersection of the ground plane and the measuring plane. Because the ground line lies within the measuring plane, its points and segments may be measured to scale. The ground line corresponds to the baseline in a linear perspective.

The viewing point is the point of projection in a linear perspective. In other...