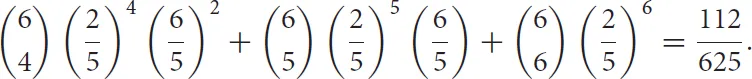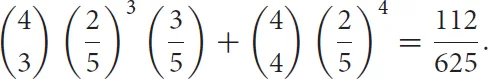The Mathematics of Various Entertaining Subjects

Research in Recreational Math

Jennifer Beineke, Jason Rosenhouse, Jennifer Beineke, Jason Rosenhouse

• Éditeur: Princeton University Press
• Année: 2015
• ISBN:
  9781400881338
• Sujet: Mathematik
• Sous-sujet: Spiele in der Mathematik

The history of mathematics is filled with major breakthroughs resulting from solutions to recreational problems. Problems of interest to gamblers led to the modern theory of probability, for example, and surreal numbers were inspired by the game of Go. Yet even with such groundbreaking findings and a wealth of popular-level books exploring puzzles and brainteasers, research in recreational mathematics has often been neglected. The Mathematics of Various Entertaining Subjects brings together authors from a variety of specialties to present fascinating problems and solutions in recreational mathematics.Contributors to the book show how sophisticated mathematics can help construct mazes that look like famous people, how the analysis of crossword puzzles has much in common with understanding epidemics, and how the theory of electrical circuits is useful in understanding the classic Towers of Hanoi puzzle. The card game SET is related to the theory of error-correcting codes, and simple tic-tac-toe takes on a new life when played on an affine plane. Inspirations for the book's wealth of problems include board games, card tricks, fake coins, flexagons, pencil puzzles, poker, and so much more.Looking at a plethora of eclectic games and puzzles, The Mathematics of Various Entertaining Subjects is sure to entertain, challenge, and inspire academic mathematicians and avid math enthusiasts alike.

PART I

Vignettes

1

SHOULD YOU BE HAPPY?

Peter Winkler

The following puzzle was tested on students from high school up to graduate level. What do you think?

You are a rabid baseball fan and, miraculously, your team has won the pennant—thus, it gets to play in the World Series. Unfortunately, the opposition is a superior team whose probability of winning any given game against your team is 60%.

Sure enough, your team loses the first game in the best-of-seven series, and you are so unhappy that you drink yourself into a stupor. When you regain consciousness, you discover that two more games have been played.

You run out into the street and grab the first passer-by. “What happened in games two and three of the World Series?”

“They were split,” she says. “One game each.”

Should you be happy?

In an experiment, about half of respondents answered “Yes—if those games hadn’t been split, your team would probably have lost them both.”

The other half argued: “No—if your team keeps splitting games, they will lose the series. They have to do better.”

Which argument is correct—and how do you verify the answer without a messy computation?

1 Comparing Probabilities

If “should you be happy” means anything at all, it should mean “are you better off than you were before?” In the above puzzle, the question comes down to: “Is your team’s probability of winning the series better now, when it needs three of the next four games, than it was before, when it needed four out of six?”

Computing and comparing tails of binomial distributions is messy but not difficult; don’t bother doing it, I’ll give you the results later. The aim here is to suggest another method of attack, which is called coupling.

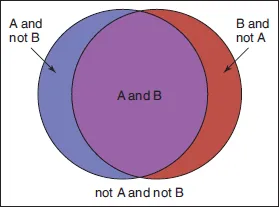
Figure 1.1. Comparing areas of the two crescents is equivalent to comparing areas of the disks.

The idea is, when you need to compare probabilities of two events A and B, to try to put them into the same experiment. All you need do is compare Pr(A but not B) with Pr(B but not A). This might be quite easy, especially if most of the time either both A and B occur or neither. The Venn diagram of Figure 1.1 illustrates the desired situation. If the blue region is larger than the red region, you deduce that A is more likely than B.

2 A Chess Problem, of Sorts

Let’s try this on a problem adapted from Martin Gardner’s legendary “Mathematical Games” column in Scientific American.¹ You want to join a certain chess club, but admission requires that you play three games against Ioana, the current club champion, and win two in a row.

Since it is an advantage to play the white pieces (which move first), you alternate playing white and black.

A coin is flipped, and the result is that you will be white in the first and third games, black in the second.

Should you be happy?

Gardner gave a (correct) algebraic proof of the answer (“no”), but, acknowledging the value of a proof by reasoning, he also provided two arguments that you’d be better off playing black first: (1) You must win the crucial middle game, thus you want to be playing white second; and (2) You must win a game as black, so you’re better off with two chances to do so.

In fact, neither argument is convincing, and even together they are not a proof.

Using coupling, you can get the answer without algebra—even if the problem is modified so that you have to win two in a row out of seventeen games, or m in a row out of n. (If n is even, it doesn’t matter who plays white first; if n is odd, you want to be black first when m is odd, white first when m is even.)

The coupling argument in the original two-out-of-three puzzle goes like this: Imagine that you are going to play four games against Ioana, playing white, then black, then white, then black. You still need to win two in a row, but you must decide in advance whether to discount the first game, or the last.

Obviously turning the first game into a “practice game” is equivalent to playing BWB in the original problem, and failing to count the last game is equivalent to playing WBW, so the new problem is equivalent to the old one.

But now the events are on the same space. For it to make a difference which game you discounted, the results must be either WWLX or XLWW. In words: if you win the first two games, and lose (or draw) the third, you will wish that you had discounted the last game; if you lose the second but win the last two, you will wish that you had discounted the first game.

But it is easy to see that XLWW is more likely than WWLX. The two wins in each case are one with white and one with black, so those cases balance; but the loss in XLWW is with black, more likely than the loss in WWLX with white. So you want to discount the first game (i.e., start as black in the original problem).

A slightly more challenging version of this argument works if you change the number of games played, and/or the number of wins needed in a row.

3 Back to Baseball

Let’s first “do the math” and see whether you should be happy about splitting games two and three. Before the news, your team needed to win four, five, or six of the next six games. (Wait, what if fewer than seven games are played? Not to worry; we are safe in imagining that all seven games are played no matter what. It doesn’t make any difference if the series is stopped when one team registers its fourth win; that, in fact, is why the rest of the games are canceled.)

The probability that your team wins exactly four of six games is “6 choose 4” (the number of ways that can happen) times (2/5)⁴ (the probability that your team wins a particular four games) times (3/5)² (the probability that the other guys win the other two). Altogether, the probability that your team wins at least four of six is

After the second and third games are split, your team needs at least three of the remaining four. The probability of winning is now

So you should be entirely indifferent to the news! The two arguments (one backward-looking, suggesting that you should be happy, the other forward-looking, suggesting that you should be unhappy) seem to have canceled each other precisely. Can this be a coincidence? Is there any way to get this result “in your head?”

Of course there is. To do the coupling a little imagination helps. Suppose that, after game three, it is discovered that an umpire who participated in games two and three had lied on his application. There is a movement to void those two games, and a countermovement to keep them. The commissioner of baseball, wise man that he is, appoints a committee to decide what to do with the results of games two and three; and in the meantime, he tells the teams to keep playing.

Of course, the commissioner hopes—and so do we puzzle-solvers—that by the time the committee makes its decision, the question will be moot...