Making Mathematics More Practical

Implementation in the Schools

Yew Hoong Leong, Eng Guan Tay, Khiok Seng Quek, Tin Lam Toh, Pee Choon Toh, Jaguthsing Dindyal, Foo Him Ho, Romina Ann Soon Yap

• Éditeur: WSPC
• Année: 2013
• ISBN:
  9789814569101
• Sujet: Matematica
• Sous-sujet: Matematica nella didattica

The book Making Mathematics Practical (published by World Scientific in 2011) proposes a new paradigm in teaching problem solving in secondary school mathematics classrooms. It is a report of the research project “Mathematical Problem Solving for Everyone” (MProSE), which attempts to provide all the necessary resources for teachers to teach problem solving in schools. This book reports as a follow-up on the actual enactment of the proposed MProSE problem solving curriculum in five Singapore schools. The experimental schools, which span across the entire spectrum of all Singapore secondary schools, report how they tweak the MProSE proposal to fit into their school curriculum, together with issues, challenges and success stories in implementing such an innovative curriculum in Singapore schools. It is an ideal handbook for educators who believe in problem solving as the core of mathematics curriculum and who wish to implement such an approach in their schools.

Contents:

• Mathematical Problem Solving for Everyone: Infusion and Diffusion (TOH Tin Lam, TAY Eng Guan, LEONG Yew Hoong, QUEK Khiok Seng, HO Foo Him, Jaguthsing DINDYAL, TOH Pee Choon)
• Mathematical Problem Solving in Temasek Junior College (YEO Chiu Jin, HSI Han Yin, Jonathan LAU Wee Lip, HO Foo Him)
• Mathematical Problem Solving in NUS High School (Grace TAN Kok Eng, Joyce SEOW Chwee Loon, TAN Boon Keong, TOH Tin Lam)
• Mathematical Problem Solving in Tanjong Katong Girls' School (CHEONG Chui Chui Hilary, Grace LEE Yun Yun, TAY Eng Guan)
• Mathematical Problem Solving in Jurong Secondary School (TEO Oi Mei, MOHAMED Faydzully On Bin Mohamed Razif, OOI Wei Yong, Simranjit KAUR, TAN Siew Hong, Jaguthsing DINDYAL)
• Mathematical Problem Solving in Bedok South Secondary School (Kavitha THAVEN, LOH Jia Perng, Samuel GOH De Hao, LIM Ming Ming, LIM Yih, Kavitha BUTHMANABAN, QUEK Khiok Seng)
• Another Step Towards Mathematical Problem Solving for Everyone (LEONG Yew Hoong, TOH Tin Lam, TAY Eng Guan, TOH Pee Choon, QUEK Khiok Seng, Jaguthsing DINDYAL, HO Foo Him)

Readership: Mathematics educators, school teachers and other facilitators.

Chapter 1

Mathematical Problem Solving for
Everyone: Infusion and Diffusion

TOH Tin Lam TAY Eng Guan LEONG Yew Hoong

QUEK Khiok Seng HO Foo Him Jaguthsing DINDYAL

TOH Pee Choon

Mathematical problem solving as the centre of mathematics learning has been the vision of the Singapore school mathematics curriculum since the 1990s. Enacting it in a school curriculum has remained a difficult enterprise. Mathematical Problem Solving for Everyone (MProSE) was a design experiment project that successfully implemented a problem solving module, based on the model described by George Pólya (1945) and enhanced with Alan Schoenfeld’s (1985) observations, in an Integrated Programme school. MProSE: Infusion and Diffusion (MInD) is a new project that intends to adapt the MProSE design to a number of mainstream schools. This chapter describes the theory underlying the MProSE design, its initial success under the MProSE project, and what needs to be done for the design to be diffused to the various schools in the MInD project.

1 Problem Solving—Central to Peripheral?

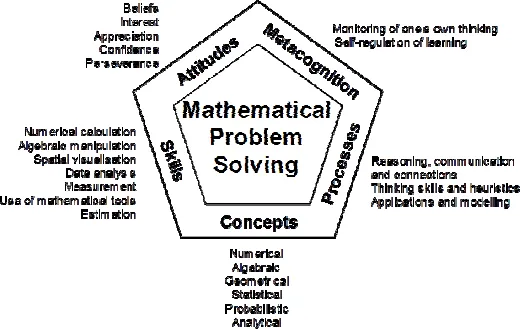
In Singapore, mathematical problem solving has been established as the central theme of the primary and secondary mathematics curriculum since the 1990s. The centrality of mathematical problem solving can also be seen in the pentagon framework (see Figure 1) of the Singapore mathematics curriculum. The Ministry of Education (MOE) syllabus document explicitly states the importance of problem solving: “Mathematical problem solving is central to mathematics learning. It involves the acquisition and application of mathematics concepts and skills in a wide range of situations, including non-routine, open-ended and real-world problems” (MOE, 2006, p. 2).

Figure 1. Singapore mathematics curriculum framework (MOE, 2006, p. 2)

Although the international comparative studies PISA and TIMSS have revealed that Singapore has achieved a high level of competence in mathematics in schools, these studies have also noted a relatively weaker performance of Singapore students in solving unfamiliar problems (Kaur, 2009). As the overarching aim of the Singapore mathematics curriculum at all levels of schooling is the development of problem solving ability, research in problem solving in school mathematics in order to support classroom practice or inform curricular policy with research-based evidence is extremely important in the Singapore context.

That problem solving is given a distinguished place in the national mathematics curriculum is not unique to Singapore. A survey of the curricula of other countries such as Australia, the United Kingdom, and the USA by Stacey (2005) revealed that problem-solving appears either as a key strand in curriculum documents or as a parallel process alongside content strands. This is indicative of the importance that the international mathematics community places on problem solving as a part of the overall development of students’ mathematical competency.

Research interest in mathematical problem solving has also been kept up over the past 50 years. As reviewed by English, Lesh and Fennewald (2008), since the seminal work of Pólya’s How to Solve It (1945), research efforts in the early years started with trialling the teaching of “Pólya-style heuristics”. It then moved on in the seventies and eighties to account for the role of other complex processes such as metacognition and affect alongside heuristic activities during problem solving (Kilpatrick, 1985; Schoenfeld, 1992), and shifted more recently to weaving problem solving approaches into standard classroom instructional practice (Silver, Ghousseini, Gosen, Charalambous, & Strawhun, 2005).

While the ideals of teaching problem solving are widely shared, there remain real challenges in enacting a curriculum centring on problem solving. A number of writers question the degree of success in the teaching of mathematical problem solving. Some assert that despite decades of curriculum development, students’ problem solving abilities still require significant improvement with respect to the changing demands of society (Kuehner & Mauch, 2006; Lesh & Zawojewski, 2007; Lester & Kehle, 2003). Similarly, Stacey (2005) noted that while some teachers around the world had some successes in teaching problem solving especially with more able students, she lamented that “there is still a great need for improvement, so that more students can gain a deeper appreciation of what it means to think mathematically and to use mathematics to assist in their daily and working lives” (p. 341).

Local studies in Singapore seem to support this picture of limited success in teaching problem solving. Koay and Foong (1996) found in their study that the Singapore lower secondary students did not relate problem solving strategies to real-world tasks; also, Foong, Yap, and Koay (1996) observed that a number of mathematics teachers expressed their lack of confidence in teaching problem solving in primary levels.

2 MProSE—Attempting to Restore the Ideal

As to the direction of problem solving research, Alan Schoenfeld wrote in the 2007 special issue of the journal ZDM on problem solving that the current focus should lie in translating decades of theory building about problem solving into workable practices in the classroom:

That body of research—for details and summary, see Lester (1994) and Schoenfeld (1985, 1992)—was robust and has stood the test of time. It represented significant progress on issues of problem solving, but it also left some very important issues unresolved. … The theory had been worked out; all that needed to be done was the (hard and unglamorous) work of following through in practical terms. (Schoenfeld, 2007, p. 539)

Our team of mathematicians and mathematics educators from the National Institute of Education, Singapore, embarked on a project, Mathematical Problem Solving for Everyone (MProSE), as an attempt at doing the “hard and unglamorous” work of realising the ideals of mathematical problem solving—as envisioned to be at the heart of the Singapore mathematics curriculum—into the daily practices of mathematics classrooms. That problem solving is currently mostly theoretical talk and not common classroom enactments is attested to by numerous local studies (see for example, Foong, Yap, & Koay, 1996; Foong, 2009).

To us, the hard and unglamorous work involved three major steps: (1) initialisation of problem solving as an essential part of the mathematics curriculum in a school at a foundational year level; (2) infusion of problem solving as an embedded regular curricular and pedagogical practice across all year levels in the school; and (3) diffusion of this innovation from one school to the full range of schools in Singapore. In each of these steps, we took a complex systems approach: instead of looming in on only one component of the system, such as curriculum, instructional practices, assessment, and teacher development, we included all these aspects in our overall design research process.

In line with design research, the initialisation stage of the process involved the creation and trialling of a design. This we did successfully with our official initial school, NUS High School. (Much work was done with Temasek Junior College even earlier but that was not formalised within the framework of a funded research project.) In that project, we redesigned parts of the curriculum and structures, including assessment practices and teacher development, within this Integrated Programme (IP) school in Singapore. [The IP schools differ from mainstream schools in that they offer a six-year programme: Year 7 to Year 12; the mainstream secondary schools offer a four-year programme which ends with the students sitting for the General Certificate Education ‘Ordinary’ (GCE ‘O’)¹ level exams.] Through a series of adjustments to the design, we developed a problem solving curriculum that is now an integral part of the school’s mathematics curriculum at the foundational level.

The MProSE design comprised a problem solving module and professional development sessions to equip teachers to deliver the module. There are ten lessons in the module and they are designed in such a way that they systematically introduce students to the language and tools used in the process of mathematical problem solving. The organizing feature and tool in these lessons is the Practical Worksheet which functions both as a pedagogical and assessment tool.

Through the Practical Worksheet, students are encouraged to follow a certain model to facilitate their problem solving process. In particular, the worksheet embeds Pólya’s (1945) four-stage model for problem solving, encouraging the students to understand the problem, devise a plan, carry out the plan, and check and expand. Also embedded in the worksheet are aspects of Schoenfeld’s (1985) framework which identify one’s cognitive resources, knowledge of heuristics, control (or metacognition), and belief systems as factors that explain one’s success or failure in problem solving. A copy of the Practical Worksheet is given in Appendix A. 1.

Table 1 gives an overview of the theme or topics discussed for the ten lessons designed in MProSE. Further details of the curriculum—a Scheme of Work, a series of lesson plans, pedagogical suggestions, and assessment strategy—are set out in the book we authored: Making Mathematics Practical: An approach to problem solving (Toh, Quek, Leong, Dindyal, & Tay, 2011). The problem solving curriculum and the research outcomes of that project are well reported in the literature. (For a full list of MProSE publications, see Appendix F.)

Table 1.

Summary of the Lessons in the MProSE module

Lesson	Lesson Theme or Topic
1	What is a problem?
2	Pólya’s problem solving strategy
3	Using heuristics to understand the problem
4	Using heuristics for a plan
5	The mathematics practical
6	Check and expand
7	More on adapting, extending and generalising
8	Schoenfeld’s framework
9	More on control
10	Revision
11	End of module assessment

Our new project, which we call MProSE: Infusion and Diffusion (MInD), thus builds upon this initial foundation of MProSE to scale out (Infuse) and scale up (Diffuse) the innovation to other schools in Singapore. MProSE thus began as the name of a project, now completed, but is henceforth taken to mean the design of a package to teach problem solving in the main curriculum of a school.

One of the key enablers of scaling innovations is a productive collaborative researcher-practitioner partnership. This is an enterprise that requires a careful cultivation and an ongoing re-commitment. In fact, according to Lemke and Sabelli (2008), “[t]he development of effective partnerships takes 5-10 years” (p 125). Seen from this perspective of partnership building, the MProSE project was the beginning of the process which MInD proposes to continue. In terms of this partnership building exercise, NUS High School (henceforth referred to as the initial school), recommitted to infusion under MInD. To avoid confusion of terms, we use MProSE from this point onwards to refer to both the earlier project and the current one. In addition, Temasek Junior College (another IP school) and three mainstream schools, Bedok South Secondary School, Jurong Secondary School and Tanjong Katong Girls’ School, agreed to work with us as well. Their stories in implementing MProSE can be read in the following chapters of this book.

The stories at this stage are mainly on the diffusion of MProSE into the schools. The design used in the initial school needed to be adjusted as it was diffused to the other schools. On the other hand, each school had to make changes (such as reorganising their curriculum and committing to teacher development for problem solving instruction) to accommodate the problem solving design. In our conception of diffusion, this notion of scalability was closely tied to sustainability. Without sustainability, there is no foundation to build upon for scaling out and scaling up. Similarly, the goal of scaling of innovations is for sustainable improvements. Such visions of sustainable innovations require systemic adjustments. We take the view that diffusion of innovations should carefully take into consideration broad scale buy-in and commitment (by teachers, school leaders and policy makers). The stories in the succeeding chapters help us to understand what have been possible and how things can be improved, both of which are important feedback features in a design experiment.

3 Description of MProSE

A description of the conceptualisation of MProSE is given in this section. It begins with the end. Over workshops and informal discussions, we asked the question of what constituted the type of student we would like our secondary school mathematics programme to produce. The answers given would almost invariably be of the following two flavours: being able to engage independently with new mathematics (independent thinker, creative, have strong mathematics content knowledge, proficient in the use of mathematics formulas, able to apply mathematics learnt and handle ‘twists’ in problems); and having a positive attitude towards mathematics (enjoy learning mathematics rather than hate it, see the beauty in mathematics, enjoy doing mathematics problems). Working backwards, we conjectured that really understanding and using the processes in problem solving would achieve the first disposition, and success in solving challenging problems and its consequent transfer to success in normal mathematics content would contribute to the latter disposition. Thus, we were drawn back to the centre of the stated mathematics curriculum, i.e. problem solving. The difficulty however lay in making the frameworks of Pólya and Schoenfeld work in the classroom.

From the MProSE team members’ personal classroom experience of teaching problem solving, students were generally resistant to following any model of problem solving – even the higher achieving students. The metacognitive part of the problem solving process still left much to be desired. In an attempt to ‘make’ the students follow through a problem solving model, especially when they were clearly struggling with the problem, a ‘Practical Worksheet’ was used in conjunction with mathematics “practical” lessons. Doing this, MProSE achieved a paradigm shift in the way students looked at these ‘difficult, unrelated’ problems which had to be done in this ‘special’ class. It was thus concluded that it is certainly conceivable that specialised lessons and materials for mathematics (similar to the science practical) may be necessary to teach the mathematical processes, including processes that are linked to problem solving. A problem solving model was needed, and George Pólya’s (1945) model (partly because Pólya’s model is already proposed in the Singapore mathematics curriculum), with Alan Schoenfeld’s (1985) enhancements, was adopted as the theoretical framework.

The mathematics practical lessons introduced by MProSE brought to the forefront of consciousness the essential stages one has to go through in mathematical problem solving. Data from the initial school clearly showed that the students were able to successfully solve the problems and even expanded on them using the Practical Worksheet. The “practical” paradigm played a critical role at the initial stages in easing the students into learning problem solving, where the learner acquires a model of problem solving and develops his own habits of problem solving.

To realise this paradigmatic change in the teaching of mathematical problem solving we had to address the issue of student assessment. What we saw as the root cause of the lack of success in previous attempts to implement problem solving in classrooms was that mathematical problem solving within the school curriculum was not assessed, especially in a way that mattered to the students. Because it was not assessed, students and teachers did not place much emphasis on the processes of problem solving; students were more interested to learn the other assessed components of the curriculum. Thus, MProSE designed a formal assessment system complementing the innovative curriculum that assesses not just the product but also the processes of problem solving. It includes an assessment rubric for assigning marks to s...