Achille e la tartaruga. Il paradosso del moto da Zenone a Einstein

Joseph Mazur, Piga C.

• Verlag: Il Saggiatore
• Jahr: 2010
• ISBN:
  9788865760482
• Thema: Matematica
• Thema: Storia e filosofia della matematica

Tre millenni fa Zenone di Elea costruì una serie di paradossi logici per provare l'impossibilità del movimento. In uno di essi sosteneva che se "congelassimo" una freccia in volo in un qualsiasi istante, essa apparirebbe ferma, e se è ferma in quell'istante lo sarà in qualunque istante. Il "crudele" Zenone (come lo definì Paul Valéry) decretò così la crisi di un basilare modello mentale, al quale continuiamo a fare ricorso per rappresentarci la realtà. L'Eleate, fra i primi, mise in relazione il movimento con lo spazio e il tempo, ponendo una domanda cruciale: il tempo e lo spazio sono continui come una linea ininterrotta oppure risultano dall'accostamento di un insieme di unità discrete come un filo di perle? Nessuna risposta trovata è tuttavia risolutiva. Da Galileo a Einstein, dal piano coordinato di Cartesio all'iperspazio di Calabi, la definizione dell'essenza del movimento ha acceso l'interesse di generazioni di "filosofi naturali", che, con tenacia, hanno provato a colmare il divario tra i loro modelli matematici e la tessitura della realtà. Un problema che il calcolo infinitesimale sembrava avere risolto, ma che nel XX secolo venne riformulato alla luce del dualismo onda-particella e che la fisica del XXI secolo - in particolare la teoria delle stringhe - potrebbe ridefinire dalle fondamenta.

TERZA PARTE

Zenone nelle sabbie del tempo

7. Un passo indietro per la misura del tempo

Ci sono cose che vediamo e altre no. La crescita di una pianta, per esempio: non riusciamo a vederla nel suo sviluppo graduale, istante dopo istante. Se vediamo una cellula vegetale dividersi, ci domandiamo come da un solo nucleo se ne siano originati due. E se vediamo un nucleo che si sdoppia, andiamo a ricercare il momento in cui un singolo cromosoma ha dato origine a due cromosomi. Ancora, nella mitosi, cioè nella divisione cellulare, andiamo a ricercare il momento in cui gli acidi nucleici e le proteine hanno compiuto la prima fase del processo di replicazione. Non importa quanto minutamente dividiamo il tempo, troviamo sempre che nello sviluppo della pianta c’è una qualche discontinuità. Si arriva sempre a un punto cui l’uno diventa due, proprio come alla fine del primo paragrafo della Genesi, quando Dio divide «la luce dalle tenebre». Torniamo così a quelle antiche questioni che Zenone e Parmenide posero per primi. La continuità è uno strumento – soltanto uno strumento – per circoscrivere il come del paradosso della freccia di Zenone. Ma Zenone ha in serbo altri interrogativi. Per un atomo che abbia sede in una delle sue frecce, gli atomi vicini sono come un universo a parte. Via via che la freccia si sposta rigidamente, quell’atomo non raggiungerà mai il suo vicino il quale, presumibilmente, si è spostato di una distanza uguale.1 Per un osservatore umano, il tempo impiegato da un atomo per spostarsi nella posizione occupata precedentemente dall’atomo contiguo è incommensurabilmente breve. Eppure, dal punto di vista dell’atomo, la distanza coperta è stata enorme. Neanche il più sensibile degli strumenti potrebbe mai osservare un tale spostamento infinitesimale. E se potesse, che dire di metà dello spostamento, o di un quarto, o di un ottavo ecc.? Quale orologio potrebbe mai cronometrare questi spostamenti?

Zenone doveva aver capito che il problema del tempo è intrecciato con il quello della continuità del movimento e che lo spazio si trova in una qualche relazione complessa non soltanto con il tempo, ma con l’osservazione: il che chiama in causa la questione della posizione di un mobile (cioè di un oggetto in movimento) in relazione a un oggetto fisso. Come si possono misurare la posizione, la velocità o le variazioni di direzione di un mobile senza far riferimento a qualcosa che sia fisso, a un sistema di riferimento, appunto?

La nostra percezione diretta del tempo e dello spazio ci dà un’idea della continuità, per quanto vaga: eppure la nostra moderna concezione della continuità va oltre ogni possibile familiarità con il mondo reale. Gli antichi matematici greci non avevano alcuna idea delle variabili algebriche continue e non avevano una definizione del continuo aritmetico paragonabile alla nostra, posto che facciamo riferimento alla retta dei numeri reali. Ci vollero 2500 anni per passare da quella concezione intuitiva della continuità che si aveva al tempo di Zenone alla sua definizione, logicamente rigorosa, fornita nel tardo XIX secolo dai matematici Augustin-Louis Cauchy, Karl Weierstrass e Richard Dedekind. Oggi si fa riferimento a una continuità che è un’astrazione, che prescinde cioè dal mondo che cade sotto i nostri sensi, e che fa riferimento alle sottigliezze dei concetti di infinitamente grande e di infinitamente piccolo, nonché a quello di convergenza di serie infinite. La continuità – che un tempo aveva come unico fondamento le impressioni visive della realtà – è oggi ridefinita nel quadro di un pensiero logico rigoroso.

Anche se gli irrazionali avevano trovato una trattazione geometrica negli Elementi di Euclide, non vennero accettati come numeri prima dell’era di Newton, quando furono utilizzati nell’ambito della cinematica, in particolare nello studio della continuità del moto. Prima della metà del XIX secolo si sapeva che la retta dei numeri razionali presenta delle lacune, anche se avrebbe destato enorme sorpresa scoprire quanto questi vuoti fossero frequenti nella retta dei numeri reali: ma i numeri razionali bastavano ai fisici e agli ingegneri per formulare previsioni riguardo al mondo reale, con approssimazioni razionali a qualunque grado di precisione.

L’insieme dei numeri reali (quei numeri che possono essere espressi con un numero di decimali potenzialmente infinito) è rappresentabile su una retta dall’insieme di punti che si estendono infinitamente nei due versi a partire da un punto rappresentativo del numero zero. Data una scala di misura, i numeri possono essere pensati come le misure delle distanze di quei punti dallo zero: i numeri negativi sono a sinistra dello zero, i positivi alla destra.

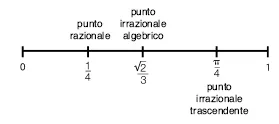
La retta dei numeri reali è una idealizzazione, a rigore non potrebbe essere tracciata, tuttavia una sua illustrazione può essere d’aiuto. Consideriamo su questa retta che si estende indefinitamente nei due versi un breve segmento, quello rappresentativo dei numeri reali da 0 a 1. Si tracci un segmento di lunghezza pari a 1. Percorrendo il segmento da sinistra a destra, l’estremo di sinistra rappresenta il numero 0; un punto alla distanza d (distante dallo 0 meno di un’unità) rappresenta il numero d. Nella figura qui sotto il punto che abbiamo notato come «1/4» dista dallo 0 un quarto della misura unitaria; il punto che abbiamo notato come «π/4» dista dallo zero di una quantità che in rapporto all’unità vale un quarto di π. In questo segmento un punto P si dice razionale se la sua distanza dall’estremo sinistro del segmento può essere espressa da una frazione della misura unitaria. I punti irrazionali sono allora quelli che si trovano a una distanza che non può essere espressa come frazione della misura unitaria.

L’insieme dei numeri razionali è un sottoinsieme relativamente piccolo dei numeri reali: è costituito infatti da quei numeri reali che possono venire espressi sotto forma di frazione o, equivalentemente, che possiedono un numero finito di cifre decimali, oppure un numero infinito di cifre decimali ma disposte con uno schema ripetuto (i numeri periodici).

Nella trattazione dei paradossi della dicotomia e di Achille, i valori dello spazio e del tempo sono entrambi considerati come misure razionali determinate in relazione alla loro rappresentazione nella retta dello spazio e del tempo, rispettivamente. Nel caso della dicotomia, la domanda è che cosa succede a distanze pari a 1/2ⁿ unità; nel caso di Achille, se le velocità dei concorrenti sono espresse da numeri razionali, e se il vantaggio iniziale della tartaruga è misurato da un numero razionale, allora ciascun punto in esame nelle argomentazioni di Zenone si trova a distanza razionale dalla linea di partenza.

Un importante interrogativo che si intravede sullo sfondo dei paradossi di Zenone sul moto è il seguente: se la punta della freccia nel suo spostamento è arrivata a un punto che sulla retta dei numeri corrisponde a un numero reale, come fa ad arrivare al punto successivo della traiettoria, dal momento che sulla retta dei numeri reali non esiste alcun punto successivo? La nozione di «punto successivo» (o «successore») non ha significato nella geometria della retta dei numeri reali (o anche soltanto dei numeri razionali). Per esempio, si consideri π, la cui rappresentazione decimale è 3,141592654... Ebbene, il seguito di cifre indicato dai puntini è infinito. Perciò qual è il successore di π? Oppure, si consideri il numero razionale 1/2, che possiamo scrivere 0,5 in notazione decimale. Bene, qual è il successore razionale di questo numero? Certo non 0,51 né 0,501 né ancora 0,5001 né alcun numero N che ci venga in mente di ottenere aggiungendo a 0,5 un seguito di cifre decimali costituito da una serie di zeri con un 1 alla fine: infatti, se considerassimo N il successore di 0,5, basterebbe introdurre un altro 0 davanti all’1 finale per trovare un altro numero, N', che si frappone tra lo zero e quel numero – N – che pensavamo fosse un successore di 0,5. Così se la punta della freccia si trova in un certo istante a metà del percorso da compiere, cioè nel punto 0,5, qual è il punto successivo in cui si troverà?

Alla fine dell’estate del 1872 Georg Kantor, professore straordinario di matematica a Halle, in Germania, ebbe la sconvolgente rivelazione che sulla retta dei numeri ci sono «molti più» punti irrazionali che punti razionali. Se sulla retta dei numeri fossero rappresentati soltanto numeri razionali, la retta presenterebbe vuoti DAPPERTUTTO! Tra ogni coppia di numeri razionali non ci sarebbe soltanto un vuoto, ma un’infinità di vuoti: segue di qui che la retta dei numeri razionali tutto potrebbe dirsi, tranne che una linea continua.

Ciò che si è detto per lo spazio può dirsi anche del tempo. Che cos’è il tempo? Qualcosa avviene e qualcosa segue. Un evento segue un altro in una sequenza che in qualche modo dev’essere possibile contenere. La punta della freccia si muove da un posto all’altro. Prima, era lì; adesso è qui; poi si troverà colà; più in là nel futuro sarà giunta a destinazione. Questi sono gli ingredienti del tempo.

Da principio gli uomini non avevano il concetto di «cinque minuti», anche se dovevano avere la nozione del tempo che trascorre con continuità dalla levata al tramonto del Sole. La precisione sarebbe venuta dopo, con l’esperienza via via accumulata e con il nascere di nuove necessità. I pesci abboccano preferibilmente il mattino, le renne pascolano nelle pianure di giorno: non sono molte le cose che si possono fare di notte. Leggiamo all’inizio della Genesi, il grande libro della creazione:2

Dio disse: «Sia la luce!» E la luce fu. Dio vide che la luce era cosa buona e separò la luce dalle tenebre e chiamò la luce giorno e le tenebre notte. Fu sera e fu mattina: primo gi...