The Learning and Teaching of Algebra

Ideas, Insights and Activities

Abraham Arcavi, Paul Drijvers, Kaye Stacey

• Editorial: Routledge
• Año: 2016
• ISBN:
  9781134820771
• Edición: 1
• Categoría: Didattica
• Categoría: Didattica generale

IMPACT (Interweaving Mathematics Pedagogy and Content for Teaching) is an exciting new series of texts for teacher education which aims to advance the learning and teaching of mathematics by integrating mathematics content with the broader research and theoretical base of mathematics education.

The Learning and Teaching of Algebra provides a pedagogical framework for the teaching and learning of algebra grounded in theory and research.

Areas covered include:

• Algebra: Setting the Scene

• Some Lessons From History

• Seeing Algebra Through the Eyes of a Learner

• Emphases in Algebra Teaching

• Algebra Education in the Digital Era

This guide will be essential reading for trainee and qualified teachers of mathematics, graduate students, curriculum developers, researchers and all those who are interested in the "problématique" of teaching and learning algebra. It allows you to get involved in the wealth of knowledge that teachers can draw upon to assist learners, helping you gain the insights that mastering algebra provides.

1

ALGEBRA—SETTING THE SCENE

Saying what algebra “is” is not a minor problem.

(Lins, 2011, p. 38)

I don’t know much about algebra, but who cares?

(Student quoted by House, 1988, p. 3)

1.1 Introduction

This chapter dwells upon two main issues: the specific aims, actions, and entities of algebra and the question of why all students should learn algebra. As such it sets the scene for the following chapters in which aims, actions, and entities as well as the “why” question are further discussed and exemplified.

1.2 Algebra—Aims, Actions, and Entities

1.2.1 Aims

Talking about the aims of algebra is tantamount to attempting to provide an answer to the question “what is algebra, and what is it for?” Despite Lins’ (2011) observation above that it is difficult to put into words what algebra is, and that “there is no Supreme Court to decide such questions” (Freudenthal, 1977, p. 193), we review some proposed answers.

The word algebra became widespread in the mid-16th century and it derives from the Arabic “Al Jabr” (or Al Jebr) as it was used by the mathematician Muhammad ibn Musa al-Khwarizmi in the title of his famous treatise on equations “Kitab al-Jabr w’al-Muqabala”—“Rules of Reintegration and Reduction” or “Restoring and Balancing” (Online Etymology Dictionary, 2001–2015). Thus, the etymology of the word evokes the main rules for solving equations.

The word algebra nowadays indicates diverse areas within mathematics such as school (“elementary”) algebra, linear algebra, and abstract algebra. The word “algebra” is also used to denote a specific structure (e.g. “an algebra over a field,” “Lie Algebra”). Sometimes it stands for operations and methods of calculations involving symbols, as in commonly heard expressions such as “do the algebra!” (Wikipedia, Algebra, 2015). Throughout this book, we refer only to algebra taught at school and the following are some of the definitions that can be applied to it.

the branch of mathematics that deals with general statements of relations, utilizing letters and other symbols to represent specific sets of numbers, values, vectors, etc., in the description of such relations.

(Dictionary.reference.com, 2012)

the branch of mathematics that deals with symbolizing general numerical relationships and mathematical structures and with operating on those structures.

(Kieran, 1992, p. 391)

the art of manipulating sums, products, and powers of [all] numbers … the manipulations may be carried out with letters standing for the numbers … the rules even apply to things … An algebraic system is … a set of elements of any sort on which … addition and multiplication operate, provided only that these operations satisfy certain rules.

(Mac Lane & Birkhoff, 1967, p. 1)

algebra involves … investigating number systems and their operations … operating with variables, solving equations, creating formulas for problem situations (algebrafication), working with functions in terms of formulas, tables and graphs, finding derivatives …

(Drijvers, Goddijn & Kindt, 2011, p. 7)

the basic ingredients of school algebra [are]: generalization of numerical and geometrical patterns and of the laws governing numerical relationships, problem solving, functional situations and modelling of physical and mathematical phenomena.

(Kieran, 2004, p. 21)

This sample of definitions is far from being exhaustive and it suggests a range of aims of algebra, which we will subsequently discuss:

• Expressing generalizations

• Establishing relationships

• Solving problems

• Exploring properties

• Proving theorems

• Calculating.

Expressing generalizations, that is, using letters to represent numbers (or other mathematical objects) in order to handle at once whole classes of numbers (or of other objects) to express a pattern or a relationship. Consider the example described in Figure 1.1. Algebra is an ideal tool to express the generalization requested.

FIGURE 1.1 Example of generalization of a pattern of dot arrangements.

Establishing relationships (some of which are functions) between numbers or quantities by means of words, formulas, tables, or graphs. For example, the relation between the amount to be paid after filling the petrol tank of a car and the amount of petrol filled can be expressed by y= ax, where y is the amount to be paid, x is the amount of petrol, and a is the price per unit (litre or gallon). If there is an extra fixed fee to be paid independently of the amount filled (for example, a night fee), say b, the relationship becomes y = ax + b.

Solving problems involving unknowns linked by operations in equations or inequalities. These problems can be posed as pure mathematical situations or in the context of modeling real life situations (in order to find answers to questions inherent to the situation). Consider, for example the problem posed in Figure 1.2.

FIGURE 1.2 Example of a problem to be solved with algebra.

Solving the equation 3x = 2.9x + 1 gives the number of gallons at which PP starts to become cheaper.

Exploring properties of operations defined by formal rules. For an example see Figure 1.3.

FIGURE 1.3 Exploring a property of an operation.

Proving theorems at school is mostly confined to geometry. However, algebra can provide many opportunities to apply deductive reasoning and at the same time establish general theorems. Consider the conjecture in Figure 1.4. This was proposed by a student in a mathematics class (Sherzer, 1973) without knowing that it had already been presented by the French mathematician Chuquet (1445–1488); nowadays it is known as the Mediant Inequality.

FIGURE 1.4 The Mediant Inequality.

Elementary number theory also provides many theorems to prove with algebra. Consider, for example, the proof that the sum of five consecutive numbers is always a multiple of 5.

Calculating. Whereas a main aim of arithmetic (if not its only one) is calculating, school algebra aspires to much more, as illustrated by the aims above. However, by virtue of its power to symbolically display general relations and structure, it also contributes to better understanding of calculation methods and even to creating new efficient and elegant methods. Consider ways to calculate 98², using the property (a – b) ² = a ² – 2ab + b ², i.e. (100 – 2)² = 100² – 2 × 100 × 2 + 2², or the property a ² – b ² = (a + b) (a – b), i.e. 98² – 2² = (98 + 2)(98 – 2). The calculation becomes very easy and can be done mentally. Also, consider the following claim: “The square of a two digit number ending in 5 always ends in 25 preceded by the product of its tens digits with its successor.” For example, 65² ends in 25 preceded by 6 × 7 = 42, namely 4225. This method can be easily justified using algebra.

1.2.2 Actions

What is it that we actually do with algebra? What are the physical and mental actions we engage in when we “do algebra”? In the following we describe the main actions involved:

• Noticing, describing, denoting, and representing

• Handling symbolic expressions

• “Unsymbolizing” and reading

• Connecting representations

• Creating algebraic expressions.

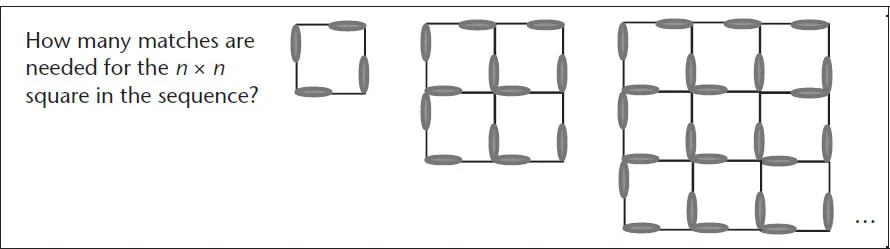
Noticing, describing, denoting, and representing regularities and patterns can be done by means of words, symbols, tables, or graphs. Consider the problem posed in Figure 1.5.

FIGURE 1.5 Example of noticing, describing, denoting, and representing patterns.

Observation would result in noticing what stays the same throughout the sequence and what changes and how. For example, it may be noticed (a) that the shapes are always squares, (b) there is a regular (linear) increase in the number of matches, and (c) the need to resist an initial tendency to calculate the total number of matches by multiplying the number of small (unit) squares by four (since internal matches would be counted twice). Some people may attempt to find the general case by counting some special cases, as indicated in Figure 1.6, and trying to generalize.

FIGURE 1.6 Number of matches for some special cases.

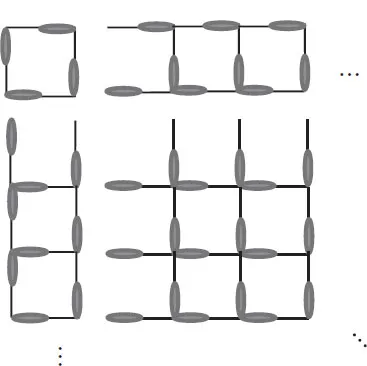
Many others will proceed to notice, describe, and represent the patterns on the basis of visually perceived regularities. For example, noticing the mistake of counting matches twice which we may avoid by decomposing the configuration as shown in Figure 1.7.

FIGURE 1.7 A decomposition of the general square.

This decomposition helps noticing that there is one shape that uses four matches, two chains (in the sides) containing n – 1 shapes using three matches and (n – 1)(n – 1) shapes using two matches, and thus the total number needed for a n × n square is 2(n ² + n).

Hershkowitz, Arcavi, and Bruckheimer (2001) illustrate several strategies based on noticing, describing, and representing patterns that support solving this task. It is worth noticing that different ways of counting may yield different forms of the algebraic expression, and thus we can engage in showing that these expressions are equivalent (in the sense described i...