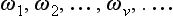History of Topology

I.M. James

• Editorial: North Holland
• Año: 1999
• ISBN:
  9780080534077
• Categoría: Mathematics
• Categoría: History & Philosophy of Mathematics

Topology, for many years, has been one of the most exciting and influential fields of research in modern mathematics. Although its origins may be traced back several hundred years, it was Poincaré who "gave topology wings" in a classic series of articles published around the turn of the century. While the earlier history, sometimes called the prehistory, is also considered, this volume is mainly concerned with the more recent history of topology, from Poincaré onwards.As will be seen from the list of contents the articles cover a wide range of topics. Some are more technical than others, but the reader without a great deal of technical knowledge should still find most of the articles accessible. Some are written by professional historians of mathematics, others by historically-minded mathematicians, who tend to have a different viewpoint.

CHAPTER 1

The Emergence of Topological Dimension Theory

Tony Crilly, Middlesex University, UK. E-mail address: [email protected]

With the Assistance of Dale Johnson^*

1. Introduction

The concept of dimension, deriving from our understanding of the dimensions of physical space, is one of the most interesting from a mathematical point of view. During the nineteenth and early twentieth century, mathematicians generalised the concept and probed its meaning. What had been a commonplace of experience became a focus for mathematical activity.

One extension of the meaning of dimension was the consideration of a mathematical space of n-dimensions. Although a revolutionary idea, the mathematical space of n-dimensions was regarded as an extrapolation from the “three dimensionality” of ordinary space. The idea of physical space being three-dimensional, an old and well accepted notion, was relatively uncontentious. While metaphysical questions concerning the meaning of four- and higher-dimensional geometry were raised, n-dimensional “hyperspace” was accepted and studied by such notable mathematicians as A.L. Cauchy (1789–1857), Arthur Cayley (1821–1895), and Hermann Grassmann (1809–1877). The principal application of “n-dimensions” in the nineteenth century was to projective and non-Euclidean geometry. Geometers studying these subjects readily accepted the notion of dimension on an intuitive basis. There was little impulse to probe the character of dimension itself.

In 1877, Georg Cantor (1845–1918) looked at dimension in a different way. He showed that the points of geometrical Figures like squares, “clearly 2-dimensional”, could be put into one-to-one correspondence with the points of straight line segments, “obviously 1-dimensional”. The “simple” idea of dimension was immediately rendered problematic. “Dimension” came under the spotlight and more sophisticated questions were asked. For instance, in what sense was dimension a geometrical invariant? Could the dimension of a space and the dimension of its image under a mapping be different?

Paradoxes and contradictions have often challenged mathematicians and led them to research many problems. The long-term result of Cantor’s paradoxical result was the development of an entire branch of topology: dimension theory. By this we principally mean topological dimension theory, that is, dimension theory free of metrical considerations. This article surveys this history, but the reader who wishes to delve further will need to consult the Selected References, in particular [16–19]. Since the appearance of these papers, other authors have considered its history and some of their works have been included in the Selected References.¹ In particular, two biographies are important: of Georg Cantor by Joseph Dauben [6] and of L.E.J. Brouwer by Walter van Stigt [36].

In essence, the three problems of defining, proving and explaining have been fundamental to the growth of topological dimension theory:

• The problem of defining the concept of dimension itself.

• The problem of proving that the dimension of mathematical spaces is invariant under certain types of mapping.

• The problem of explaining the number of dimensions of physical space.

The first and second problems, mathematical in nature, have been the most important direct influence on the growth of the theory of dimension. The third, a problem of physics or cosmology, has provided an indirect but significant motivation for the development of the theory from outside the mathematical domain.

2. Early history

The definitional problem seeking to answer the question “what is dimension?” is detectable in the writings of the Greek philosophers and mathematicians. To indicate that “dimension” has ancient roots we mention two of the most prominent authors.

According to Euclid, a point is that which has no part, a line is breadthless length, and a surface is that which has length and breadth only (Book I). A solid is that which has length, breadth and depth (Book XI). Euclid’s definitions show a concern for a rudimentary “theory of dimension” by the recognition of a “dimension” hierarchy in the sequence of primary geometrical objects: point, line, surface, solid. A passage from Aristotle’s On the Heavens shows a similar motivation. In it, Aristotle is more definite, even if its tone is more metaphysical:

Of magnitude that which (extends) one way is a line, that which (extends) two ways a plane, and that which (extends) three ways a body. And there is no magnitude besides these, because the dimensions are all that there are, and thrice extended means extended all ways. For, as the Pythagoreans say, the All and all things in it are determined by three things; end, middle and beginning give the number of the All, and these give the number of the Triad [17, p. 104].

Other eminent philosophers and scientists considered questions about dimension including Galilei Galileo (1564–1642), Gottfried Wilhelm Leibnitz (1646-1716) and Immanuel Kant (1724–1804). While all of these touched on dimension in some form or other, there is no suggestion that they sought to create anything like modern dimension theory or that they were working towards modern dimension theory as it stands today. Dimension theory is primarily a modern subject of mathematics; its main historical roots lie in the early nineteenth century when the Bohemian priest Bernard Bolzano (1781–1848) examined several facets of the definitional problem and proposed some interesting solutions.

Bolzano sought precise definitions of geometrical objects. “At the present time”, he wrote in 1810, “there is still lacking a precise definition of the most important concepts: line, surface, solid” [16, p. 271]. This dull essentialist problem of definitions, conceived within the limits of Euclidean geometry, led him to break from the bonds of traditional geometry. Bolzano stressed the theoretical role of mathematics and its “usefulness” in exercising and sharpening the mind. Rigour in pure mathematics was uppermost in his thoughts. For example, he regarded it a mistake to make any appeal to motion as it was foreign to pure geometry. This purge of motion from geometry is relevant to Bolzano’s dimension-theoretic definitions of line, surface, and solid. For instead of taking a line as the path of a moving point, as for example was done by Abraham Kästner (1719–1800), Bolzano attempted to define the concept of line independently of any idea of motion.

A basic feature of Bolzano’s outlook on research in mathematics was his view that mathematics stands in close relation to philosophy. “My special pleasure in mathematics rests only in its purely speculative part”, admitted Bolzano in his autobiographical writings [16, p. 263]. His youthful Betrachtungen is heavily imbued with philosophy and this illustrated his deep concern for the logical and foundational issues in mathematics. Bolzano’s concern over definitions required that he seek the “true” definitions for the objects of geometry. Undoubtedly, this essentialist philosophy is to blame for the main shortcomings of his geometrical investigations. The end product of his research, a seemingly endless string of definitions with hardly a theorem, must be regarded as disappointing. Yet if one asks “what is” questions – What is a line?, What is a continuum? – then one must expect essentialist answers. But, while definitions have a certain value in mathematics, no fruitful mathematical theory can consist entirely of them. Theorems and their proofs which relate definitions one to another, are much more important. Bolzano’s theory is unquestionably lacking in these.

Bolzano returned to geometrical studies in the 1830s and 1840s. In writings of 1843 and 1844, though not published in his lifetime, he revised and improved his youthful findings. In these, Bolzano’s topological basis, derived from his concept of “neighbour” and “isolated point”, is very deep. The concept of neighbour, which in effect uses the modern notion of the boundary of a spherical neighbourhood allowed Bolzano to put forward some very clear definitions of line, surface, and solid. Later, when he discovered his notion of isolated point, he was able to arrive at an even deeper understanding of the basic Figures of geometry. His geometrical insights were far more penetrating than those of his contemporaries.

3. Cantor’s “paradox” of dimension

While Bolzano could be regarded as a precursor, there is little doubt that Georg Cantor is the true father of dimension theory. In 1877 Cantor discovered to his own amazement that the points of a unit line segment could be put into one-to-one correspondence with the points of a unit square or even more generally with the points of a q -dimensional

Georg Cantor (1845–1918)

cube. Cantor’s probing led him to exclaim to his friend Richard Dedekind (1831–1916): “As much as you will not agree with me, I can only say: I see it but I do not believe it” [3, p. 44]. The strange result immediately called into question the very concept of dimension. Was it well-defined or even meaningful?

Cantor’s work on set theory arose out of his investigations into the uniqueness of representing a function by a trigonometric series. In 1874 he published his first purely set-theoretic paper, giving proofs that the set of real algebraic numbers could be conceived in the form of an infinite sequence:

This set is countable (abzählbar, to use Cantor’s later term), while the set of all real numbers is uncountable and cannot be listed in this way. Through these results on “linear sets” Cantor saw a clear distinction between two types of infinite sets of numbers on the real number line.

As his correspondence with Dedekind shows, Cantor discovered these results in 1873. Cantor had met Dedekind by chance in Gersau during a trip to Switzerland in 1872 and their famous exchange of letters ensued [7, 8, 10, 23]. From his discoveries about linear sets of points it was perfectly natural for Cantor to wonder whether there were different types of infinite sets in the plane or in higher-dimensional spaces. In a letter to Dedekind dated 5 January 1874 he posed a tantalising new research question, a question which is basic to the growth of dimension theory:

Can a surface (perhaps a square including its boundary) be put into one-to-one correspondence with a line (perhaps a straight line segment including its endpoints) so that to each point of the surface there corresponds a point of the line and conversely to each point of the line there corresponds a point of the surface? [17, p. 132]

From the start Cantor was convinced of the importance and difficulty of this question. He realised that most mathematicians would regard the impossibility of such a correspondence as so obvious as not to require proof. When he discussed it with a friend in Berlin during the first part of 1874, the friend explained that the matter was absurd “since it is obvious that two independent variables cannot be reduced to one” [17, p. 132]. In relating this encounter to Dedekind in a letter of 18 May, the young Cantor sought reassurance that he was not chasing a delusion! In posing his question Cantor introduced something quite new and important into thinking about dimension: he related mappings and correspondences to the dimension of Figures and spaces. For Cantor this was a natural relation because he was interested in cardinality.

It is likely that Cantor only worked intermittently on this question from May 1874 until April 1877 and indeed without success. However, he persisted in regarding it as important. When he attended the Gaussjubiläum in Göttingen on 30 April 1...

Índice

• Cover image
• Title page
• Table of Contents
• Copyright
• Preface
• Acknowledgement of Illustrations
• Chapter 1: The Emergence of Topological Dimension Theory
• Chapter 2: The Concept of Manifold, 1850–1950
• Chapter 3: Development of the Concept of Homotopy
• Chapter 4: Development of the Concept of a Complex
• Chapter 5: Differential Forms
• Chapter 6: The Topological Work of Henri Poincaré
• Chapter 7: Weyl and the Topology of Continuous Groups
• Chapter 8: By Their Fruits Ye Shall Know Them: Some Remarks on the Interaction of General Topology with Other Areas of Mathematics
• Chapter 9: Absolute Neighborhood Retracts and Shape Theory
• Chapter 10: Fixed Point Theory
• Chapter 11: Geometric Aspects in the Development of Knot Theory
• Chapter 12: Topology and Physics – a Historical Essay
• Chapter 13: Singularities
• Chapter 14: One Hundred Years of Manifold Topology
• Chapter 15: 3-Dimensional Topology up to 1960
• Chapter 16: A Short History of Triangulation and Related Matters
• Chapter 17: Graph Theory
• Chapter 18: The Early Development of Algebraic Topology
• Chapter 19: From Combinatorial Topology to Algebraic Topology
• Chapter 20: π3(S2), H. Hopf, W.K. Clifford, F. Klein
• Chapter 21: A History of Cohomology Theory
• Chapter 22: Fibre Bundles, Fibre Maps
• Chapter 23: A History of Spectral Sequences: Origins to 1953
• Chapter 24: Stable Algebraic Topology, 1945–1966
• Chapter 25: A History of Duality in Algebraic Topology
• Chapter 26: A Short History of H-spaces
• Chapter 27: A History of Rational Homotopy Theory
• Chapter 28: History of Homological Algebra
• Chapter 29: Topologists at Conferences
• Chapter 30: Topologists in Hitler’s Germany
• Chapter 31: The Japanese School of Topology
• Chapter 32: Some Topologists
• Chapter 33: Johann Benedikt Listing
• Chapter 34: Poul Heegaard
• Chapter 35: Luitzen Egbertus Jan Brouwer: 27.2.1881 Overschie – 2.12.1966 Blaricum
• Chapter 36: Max Dehn
• Chapter 37: Jakob Nielsen and His Contributions to Topology
• Chapter 38: Heinz Hopf
• Chapter 39: Hans Freudenthal: 17 September 1905 – 13 October 1990
• Chapter 40: Herbert Seifert: May 27, 1907 – October 1, 1996
• Appendix: Some Dates
• Index