Elementos. Libros X-XIII

Euclides, María Luisa Puertas Castaños

• Editorial: Gredos
• Año: 2016
• ISBN:
  9788424932534
• Categoría: Literatura
• Categoría: Colecciones literarias antiguas y clásicas

Tanto para expertos como para novicios, el nombre "Euclides" se ha convertido en sinónimo de geometría.Euclides estableció lo que se convertiría en la forma clásica de una proposición matemática: un enunciado deducido lógicamente a partir de unos principios previamente aceptados. En el caso de los Elementos, los principios que se toman como punto de partida son veintitrés definiciones, cinco postulados y cinco axiomas o nociones comunes.El enorme magisterio de los Elementos se ha mantenido hasta hoy, pues buena parte de su contenido se sigue impartiendo en las escuelas; sin embargo, las aportaciones de la geometría moderna le han arrebatado la exclusividad: desde el siglo XIX se han definido geometrías consistentes, llamadas "no euclidianas", a partir de la supresión o modificación del quinto axioma, el de las paralelas. Sin embargo, la misma denominación de estas variantes contemporáneas indica que, tanto para expertos como para novicios, el nombre "Euclides" se ha convertido en sinónimo de geometría.

LIBRO DÉCIMO

DEFINICIONES

1. Se llaman magnitudes conmensurables aquellas que se miden con la misma medida, e inconmensurables aquellas de las que no es posible que haya una medida común.

2. Las líneas rectas son conmensurables en cuadrado cuando sus cuadrados se miden con la misma área, e inconmensurables cuando no es posible que sus cuadrados tengan un área como medida común ¹ .

3. Dados estos supuestos, se demuestra que hay un número infinito de rectas respectivamente conmensurables e inconmensurables, unas sólo en longitud y otras también en cuadrado con una recta determinada. Llámese entonces racionalmente expresable la recta determinada; y las conmensurables con ella, bien en longitud y en cuadrado, bien sólo en cuadrado, racionalmente expresables y las inconmensurables con ella llámense no racionalmente expresables ² .

4. Y el cuadrado de la recta determinada (llámese) racionalmente expresable, y los cuadrados conmensurables con éste racionalmente expresables; pero los inconmensurables con él llámense no racionalmente expresables; y las rectas que los producen (llámense) no racionalmente expresablas, a saber, si fueran cuadrados, los propios lados y si fueran otras figuras rectilíneas, aquellas (rectas) que construyan cuadrados iguales a ellos ³ .

PROPOSICIÓN 1

Dadas dos magnitudes desiguales, si se quita de la mayor una (magnitud) mayor que su mitad y, de la que queda, una magnitud mayor que su mitad y así sucesivamente, quedará una magnitud que será menor que la magnitud menor dada.

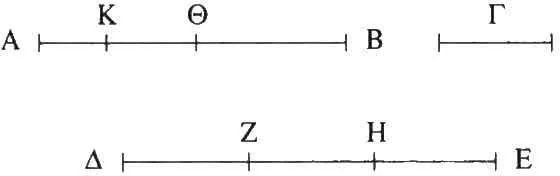
Sean AB , Γ dos magnitudes desiguales de las cuales AB es la mayor.

Digo que, si se quita de AB una (magnitud) mayor que su mitad y de la (magnitud) restante, una (magnitud) mayor que su mitad, y así sucesivamente, quedará una magnitud que será menor que la magnitud Γ .

Pues Γ multiplicada será alguna vez mayor que AB [V Def. 4]. Multiplíquese y sea ΔE un múltiplo de Γ mayor que AB ; divídase ΔE en ΔZ , ZH , HE iguales a Γ , y de AB quítese BΘ mayor que su mitad, y de AΘ (quítese) ΘK mayor que su mitad, y así sucesivamente hasta que las divisiones de AB lleguen a ser iguales en número a las divisiones de ΔE .

Sean, pues, AK , KΘ , ΘB divisiones que son iguales en número a las (divisiones) ΔZ , ZH , HE ; ahora bien, dado que ΔE es mayor que AB y que de ΔE se ha quitado la (magnitud) EH menor que su mitad y de AB la (magnitud) BΘ mayor que su mitad, entonces la magnitud restante HΔ es mayor que la (magnitud) restante ΘA . Y dado que HΔ es mayor que ΘA y se ha quitado de HΔ su mitad HZ y de ΘA una (magnitud) ΘK mayor que su mitad, entonces la (magnitud) restante ΔZ es mayor que la (magnitud) restante AK . Pero ΔZ es igual a Γ ; luego es mayor que AK . Por tanto, AK es menor que Γ .

Por consiguiente, de la magnitud AB queda la magnitud AK que es menor que la magnitud dada Γ . Q . E . D . De manera semejante demostraríamos que (esto ocurre) también si se quita la mitad ⁴ .

PROPOSICIÓN 2

Si al restar continua y sucesivamente la menor de la mayor de dos magnitudes desiguales, la restante nunca mide a la anterior, las magnitudes serán inconmensurables.

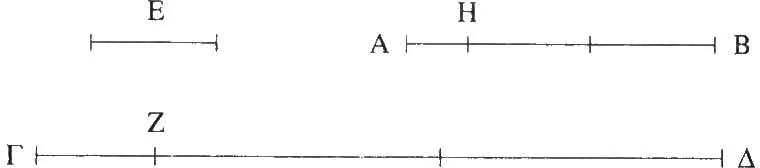
Habiendo, pues, dos magnitudes desiguales AB , ΓΔ y (siendo) AB la menor, al restar sucesivamente la menor de la mayor, no mida nunca la (magnitud) restante a la anterior a ella.

Digo que las magnitudes AB , ΓΔ son inconmensurables.

Pues, si son conmensurables, alguna magnitud las medirá. Mídalas (una magnitud), si es posible, y sea E ; y AB , al medir a ZΔ , deje la magnitud ΓZ menor que ella, y ΓZ , al medir a BH , deje AH menor que ella, y repítase así sucesivamente hasta que quede una magnitud que sea menor que E . Sea así y quede AH menor que E . Así pues, como E mide a AB y AB mide a ΔZ , entonces E también medirá a ZΔ . Pero mide también a la magnitud entera ΓΔ ; luego medirá también a la magnitud restante ΓZ . Ahora bien, ΓZ mide a BH ; entonces E también mide a BH . Pero mide también a la (magnitud) entera AB ; así que medirá también a la (magnitud) restante AH , la mayor a la menor; lo cual es imposible. Luego ninguna magnitud medirá a las magnitudes AB , ΓΔ ; por tanto, las magnitudes AB , ΓΔ son inconmensurables [X Def. 1].

Por consiguiente, si de dos magnitudes desiguales..., etc. ⁵ .

PROPOSICIÓN 3

Dadas dos magnitudes conmensurables, hallar su medida común máxima.

Sean AB , ΓΔ dos magnitudes dadas conmensurables, de las cuales AB sea la menor.

Así pues, hay que hallar la medida común máxima de AB , ΓΔ .

Pues bien, AB o mide a ΓΔ o no la mide. Si, en efecto, la mide y se mide también a sí misma, entonces AB es una medida común de AB , ΓΔ ; y está claro que también es la mayor. Porque no medirá a AB ninguna magnitud mayor que AB .

Pero ahora no mida AB a ΓΔ y, al restar continua y sucesivamente la menor de la mayor, la (magnitud) restante medirá alguna vez a la anterior a ella, porque AB , ΓΔ no son inconmensurables [X 2]; y AB , al medir a EΔ , deje la (magnitud) EΓ menor que ella, y EΓ , al medir a ZB , deje la (magnitud) AZ menor que ella y mida AZ a ΓE .

Como, en efecto, AZ mide a ΓE ,...

Índice

• Anteportada
• Portada
• Página de derechos de autor
• NOTA DE LA TRADUCTORA
• LIBRO X
• LIBRO XI
• LIBRO XII
• LIBRO XIII
• ÍNDICE