Solid Biomechanics

Roland Ennos

• Editorial: Princeton University Press
• Año: 2011
• ISBN:
  9781400840649
• Categoría: Ciencias biológicas
• Categoría: Biofísica

Solid Biomechanics is the first book to comprehensively review the mechanical design of organisms. With a physical approach and a minimum of mathematics, the textbook introduces readers to the world of structural mechanics and sheds light on the dazzling array of mechanical adaptations that link creatures as dissimilar as bacteria, plants, and animals. Exploring a wide range of subjects in depth, from spider silks and sharkskin to climbing plants and human food processing, this immensely accessible text demonstrates that the bodies of animals and plants are masterpieces of engineering, enabling them to survive in a hostile world.
The textbook describes how organisms construct materials from limited components, arrange materials into efficient structures that withstand different types of stresses, and interact mechanically with their environment. Looking at practical and historical aspects of the subject, the book delves into how the mechanics of organisms might be applied to other engineering scenarios and considers the ways structural biomechanics could and should develop in the future if more is to be learned about the form and function of organisms. Solid Biomechanics will be useful to all those interested in how organisms work, from biologists and engineers to physicists and students of biomechanics, bionics, and materials science.

• The first comprehensive review of the structural mechanics of organisms
• Introduces the subject using a physical approach involving minimal mathematics
• Three complementary sections: materials, structures, and mechanical interactions of organisms
• Links the dazzling array of mechanical adaptations seen in widely differing organisms
• Practical and historical approach shows how mechanical adaptations have been discovered and how readers can perform their own investigations

PART 1

Understanding Elasticity

CHAPTER 1

The Properties of Materials

FORCES: DYNAMICS AND STATICS

We all have some intuitive idea about the mechanics of the world around us, an idea built up largely from our own experience. However, a proper scientific understanding of mechanics has taken centuries to achieve. Isaac Newton was of course the founder of the science of mechanics; he was the first to describe and understand the ways in which moving bodies behave.

Introducing the concepts of inertia and force, he showed that the behavior of moving bodies could be summed up in three laws of motion.

1) The law of inertia: An object in motion will remain in motion unless acted upon by a net force. The inertia of an object is its reluctance to change its motion.

2) The law of acceleration: The acceleration of a body is equal to the force applied to it divided by its mass, as summarized in the equation

where F is the force; m, the mass; and a, the acceleration.

3) The law of reciprocal action: To every action there is an equal and opposite reaction. If one body pushes on another with a given force, the other will push back with the same force in the opposite direction.

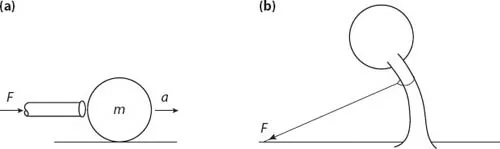
To summarize with a simple example: if I give a push to a ball that is initially at rest (fig. 1.1a), it will accelerate in that direction at a rate proportional to the force and inversely proportional to its mass. The great step forward in Newton’s scheme was that, together with the inverse square law of gravity, it showed that the force that keeps us down on earth is one and the same with the force that directs the motion of the planets.

All this is a great help in understanding dynamic situations, such as billiard balls colliding, guns firing bullets, planets circling the sun, or frogs jumping. Unfortunately it is much less useful when it comes to examining what is happening in a range of no-less-common everyday situations. What is happening when a book is lying on a desk, when a light bulb is hanging from the ceiling, or when I am trying to pull a tree over? (See fig. 1.1b.) In all of these static situations, it is clear that there is no acceleration (at least until the tree does fall over), so the table or rope must be resisting gravity and the tree must be resisting the forces I am putting on it with equal and opposite reactions. But how do objects supply that reaction, seeing as they have no force-producing muscles to do so? The answer lies within the materials themselves.

Figure 1.1. Forces on objects in dynamic and static situations. In dynamic situations, such as a pool ball being given a push with a cue (a), the force, F, results in the acceleration, a, of the ball. In static situations, such as a tree being pulled sideways with a rope (b), there is no acceleration.

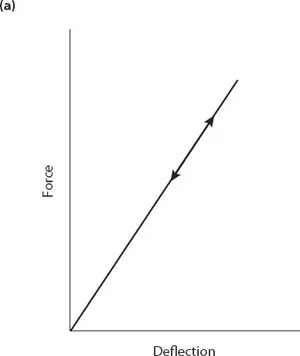
Robert Hooke (1635–1703) was the first to notice that when springs, and indeed many other structures and pieces of material, are loaded, they change shape, altering in length by an amount approximately proportional to the force applied, and that they spring back into their original shape after the load is removed (fig. 1.2a). This linear relationship between force and extension is known as Hooke’s law.

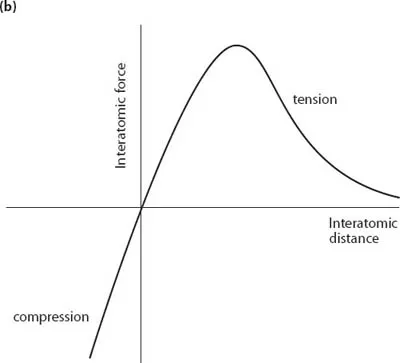
What we now know is that all solids are made up of atoms. In crystalline materials, which include not only salt and diamonds but also metals, such as iron, the atoms are arranged in ordered rows and columns, joined by stiff interatomic bonds. If these sorts of materials are stretched or compressed, we are actually stretching or compressing the interatomic bonds (fig. 1.2b). They have an equilibrium length and strongly resist any such movement. In typically static situations, therefore, the applied force is not lost or dissipated or absorbed. Instead, it is opposed by the equal and opposite reaction force that results from the tendency of the material that has been deformed to return to its resting shape. No material is totally rigid; even blocks of the stiffest materials, such as metals and diamonds, deform when they are loaded. The reason that this deformation was such a hard discovery to make is that most structures are so rigid that their deflection is tiny; it is only when we use compliant structures such as springs or bend long thin beams that the deflection common to all structures is obvious.

The greater the load that is applied, the more the structure is deflected, until failure occurs; we will then have exceeded the strength of our structure. In the case of the tree (fig. 1.1b), the trunk might break, or its roots pull out of the soil and the tree accelerate sideways and fall over.

INVESTIGATING THE MECHANICAL PROPERTIES OF MATERIALS

The science of elasticity seeks to understand the mechanical behavior of structures when they are loaded. It aims to predict just how much they should deflect under given loads and exactly when they should break. This will depend upon two things. The properties of the material are clearly important—a rod made of rubber will stretch much more easily than one made of steel. However, geometry will also affect the behavior: a long, thin length of rubber will stretch much more easily than a short fat one.

Figure 1.2. When a tensile force is applied to a perfectly Hookean spring or material (a), it will stretch a distance proportional to the force applied. In the material this is usually because the bonds between the individual atoms behave like springs (b), stretching and compressing by a distance that at least at low loads is proportional to the force applied.

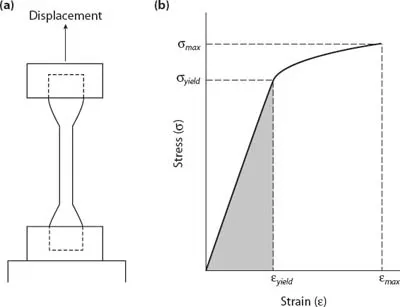
Figure 1.3. In a tensile test, an elongated piece of a material is gripped at both ends (a) and stretched. The sample is usually cut into a dumbbell shape so that failure does not occur around the clamps, where stresses can be concentrated. The result of such a test is a graph of stress against strain (b), which shows several important mechanical properties of the material. The shaded area under the graph is the amount of elastic energy the material can store.

To understand the behavior of materials, therefore, we need to be able separate the effects of geometry from those of the material properties. To see how this can be done, let us examine the simplest possible case: a tensile test (fig. 1.3a), in which a uniform rod of material, say a rubber band, is stretched.

The Concept of Stress

If it takes a unit force to stretch a rubber band of a given cross-sectional area a given distance, it can readily be seen that it will take twice the force to give the same stretch to two rubber bands set side by side or to a single band of twice the thickness. Resistance to stretching is therefore directly proportional to the cross-sectional area of a sample. To determine the mechanical state of the rubber, the force applied to the sample must consequently be normalized by dividing it by its cross-sectional area. Doing so gives a measurement of the force per unit area, or the intensity of the force, which is known as stress and which is usually represented by the symbol σ, so that

where P is the applied load and A the cross-sectional area of the sample. Stress is expressed in SI units of newtons per square meter (Nm⁻²) or pascals (Pa). Unfortunately, this unit is inconveniently small, so most stresses are given in kPa (Nm⁻² × 10³), MPa (Nm⁻² × 10⁶), or even GPa (Nm⁻² × 10⁹).

The Concept of Strain

If it takes a unit force to stretch a rubber band of a given length by a given distance, the same force applied to two rubber bands joined end to end or to a single band of twice the length will result in twice the stretch. Resistance to stretching is therefore inversely proportional to the length of a sample. To determine the change in shape of the rubber as a material in general, and not just of this sample, the deflection of the sample must consequently be normalized by dividing by its original length. This gives a measure of how much the material has stretched relative to its original length, which is known as strain and which is usually represented by the symbol, ε, so that

where dL is the change in length and L the original length of the sample. Strain has no units because it is calculated by dividing one length by another.

It is perhaps unfortunate that engineers have chosen to give the everyday words stress and strain such precise definitions in mechanics, since doing so can confuse communications between engineers and lay people who are used to the vaguer uses of these words. As we shall see, similar confusion can also be a problem with the terms used to describe the mechanical properties of materials.

DETERMINING MATERIAL PROPERTIES

Many material properties can be determined from the results of a tensile test once the graph of force against displacement has been converted with equations 1.2 and 1.3 into one of stress versus strain. Figure 1.3b shows the stress-strain curve for a typical tough material, such as a metal. Like many, but by no means all, materials, this one obeys Hooke’s law, showing linear elastic behavior: the stress initially increases rapidly in direct proportion to the strain. Then the material reaches a yield point, after which the stress increases far more slowly, until finally failure occurs and the material breaks.

The first important property that can be derived from the graphs is the stiffness of the material, also known as ...

Índice

• Cover
• Title
• Copyright
• Contents
• Preface
• Acknowledgments
• Part 1 Understanding Elasticity
• Part 2 Biological Materials
• Part 3 Biological Structures
• Part 4 Mechanical Interactions
• Part 5 Looking Forward
• Glossary
• References
• Index