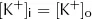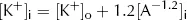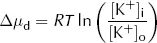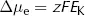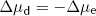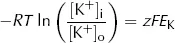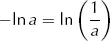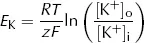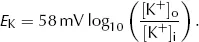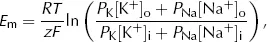A Thinking Approach to Physiology

Ian N Sabir, Juliet A Usher-Smith

• Editorial: WSPC
• Año: 2008
• ISBN:
  9789814365420
• Categoría: Biowissenschaften
• Categoría: Physiologie

Whereas other fields continue to become more complex and specialized, physiology happily remains an area that can still be understood by thinking from first principles. However, given the increasing quantity of information available today, it is easy to become overly concerned with details and give in to the temptation to memorize rather than understand. In this concise book, the authors convey their enthusiasm for physiology and convincingly persuade the reader that with a sound understanding of principles, details often fall effortlessly into place. It is by no means an attempt to produce another comprehensive textbook. Instead, a broad overview of the subject is presented, covering areas that are not given the attention they deserve in other texts whilst purposely omitting those aspects where memorization is an unfortunate necessity.

Contents:

• Electrical Properties of Cells
• Muscle as an Excitable Tissue
• The Digestive System
• The Respiratory System
• The Circulatory System
• The Kidney and Body Fluids
• Integrative Physiology
• Derivations and Theoretical Points

Readership: Medical, dental and veterinary undergraduates.

CHAPTER 1

Electrical Properties of Cells

---

All multicellular life forms face the complex problem of ensuring that the behaviour of each cell supports the continued function of the entire organism. To this end, intercellular (cell to cell) communication is of paramount importance. Animals have evolved two interacting strategies: chemical and electrical signalling. Chemical signals, secreted by one cell and acting on another, may act locally on neighbouring cells (paracrine factors) or be transported in the bulk circulation to act on distant cells (endocrine factors or hormones). An advantage of this strategy is that signals can be sent to large numbers of cells at the same time. Furthermore, by expressing different receptors, individual cells can respond differently to the same chemical signals. The main disadvantage of chemical signals is that they take a rather long time to act, but this is useful where sustained responses are required. In contrast, electrical signals are highly specific to their target cells and act rapidly to bring about transient responses. There are additionally important interactions between these two modes of signalling: electrical signals frequently trigger chemical signals, which may then go on to trigger further electrical signals.

This chapter focuses on electrical signalling and discusses how these signals are set up and transmitted around the body. Such signalling requires neurons to act as electrical conducting wires, passing current longitudinally between two points. Since a current is a flow of charge, it must be driven by an energy difference (potential difference) between the two points. Such potential differences exist transversely across the membranes of all cells at rest (resting potentials). However, electrical signalling requires that the cells involved be capable of altering this potential difference, usually moving from being inside-negative at rest to inside-positive, as a result of the movement of charge across their membranes. This change in potential difference is described as depolarisation and the ability to depolarise defines excitable cells such as nerve and muscle. Here, we first consider how the resting potential arises and then go on to describe the process of depolarisation and discuss how the signals set up are transmitted around the body.

1.1 The Resting Membrane Potential

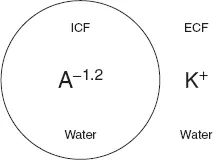
To understand how a potential difference arises across a cell membrane at rest we only need to think of a cell in very simple terms. We can begin by imagining it as nothing more than a bag of protein, which we will call A. The cell membrane must be impermeable to A so that it does not leak out of the cell. Like other proteins and buffers, A is capable of gaining and loosing H⁺ ions. The pKa of A, the pH at which half of A is capable of gaining H⁺ and half is capable of loosing H⁺ (see Chapter 7), is around 6.2. Intracellular pH is around 7.2 and at this higher (more alkaline) pH, A will tend to loose H⁺ and become negatively charged. In fact, at pH 7.2, A has a mean charge of −1.2 (A^−1.2). It is because of this charge on A that a potential difference arises across cell membranes at rest (commonly referred to as the resting potential, resting Em). To understand why, we can imagine a situation where the intracellular fluid (ICF) contains only A^−1.2 and water while the extracellular fluid (ECF) contains only K⁺ and water (Fig. 2).

At rest, cell membranes can be assumed to be freely permeable to K⁺. From the point of view of diffusion, the lowest energy state will therefore be reached when the concentration of K⁺ is the same on both the inside ([K⁺]i) and outside ([K⁺]o) of the membrane, i.e.

However, from the point of view of electric charge, the lowest energy state will be reached when the charge inside the cell equals the charge outside the cell. Remembering the charge on A, this will occur when:

Fig. 2. Simple model cell.

Clearly both the above conditions cannot be met at the same time as [K⁺]i cannot both be the same as [K⁺]o and greater than [K⁺]o. At equilibrium, [K⁺]i will therefore lie somewhere between these two values. At this equilibrium, there will still be an energy gradient for K⁺ to leave the cell from a diffusive (concentration) point of view and an energy gradient for K⁺ to enter the cell from an electrical point of view, but these two will balance. It is this persistent electrical gradient, arising from the difference in charge between one side of the membrane and the other, that gives rise to the resting E_m. By equating these two energy gradients, we can obtain an equation for the resting E_m.

For each mole of K⁺, the diffusive energy gradient tending to make K⁺ leave the cell at equilibrium is given by:

where Δµ_d = diffusive energy gradient per mole of K⁺ (J·mol⁻¹)

R = ideal gas constant (6.31 J·mol⁻¹·K⁻¹)

T = absolute temperature (K)

Thus the energy per mole of K⁺ is proportional to the logarithm of relative K⁺ concentrations on each side of the membrane, with R and T together constituting the constant of proportionality. The electrical energy gradient tending to make K⁺ enter the cell at equilibrium is given by:

where Δµe = electrical energy gradient per mole of K⁺ (J·mol⁻¹)

z = charge on K⁺ (its valency, +1)

F = Faraday constant (96500 C·mol⁻¹)

EK = equilibrium potential difference for K⁺ (V)

The reasoning underlying this equation is rather straightforward. Here the cell membrane is in effect being treated as a capacitor, a device which stores charge. As we show in the Appendix, the energy stored by a capacitor depends on the difference in charge (given by zF for each mole of ions) and the potential difference across it (EK).

At equilibrium, there is no net energy gradient for K⁺ movement so the two energy differences must balance. This means that:

and

Since

this can be rearranged to

which is the Nernst equation. This gives the equilibrium (Nernst) potential difference across a membrane which is permeable only to one ion, in this case K⁺. Note that this equilibrium potential depends only on the relationship between [K⁺]i and [K⁺]o. Providing the membrane remains permeable to K⁺, altering the permeability does not alter the equilibrium potential.

Putting standard values of R (6.31 J·mol⁻¹·K⁻¹), T (298K), z (+1) and F (96500 C·mol⁻¹) and converting from ln to log₁₀ gives:

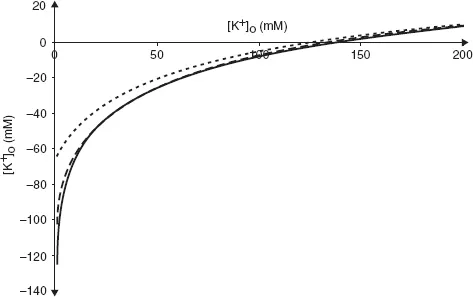
Unsurprisingly, real cells are not quite so simple. Cell membranes are permeable not only to K⁺ but also to other ions. Of these, only Na⁺ makes a significant contribution to the resting E_m. We can see the effect this has by plotting experimentally measured values of resting E_m against [K⁺]o at two different values of [Na⁺]o (Fig. 3).

Even when [Na⁺]o is at its physiological value in humans (140 mM, broken line) the curve deviates from the values of EK calculated using the equation above, especially when [K⁺]o is low. When [Na⁺]o is raised to 1000 mM, there is a large difference between the observed curve and that of which the Nernst equation predicts.

Fig. 3. Relationship between E_m and [K+]_o. Solid line is the prediction from the Nernst equation, broken line shows measured values at physiological levels of [Na+]_o and dotted line shows measured values at [Na+]o = 1000 mM.

We can account for this contribution from Na⁺ in a modified form of the Nernst equation, the Goldman equation

where P_Na is the ...