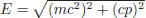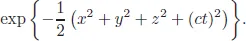New Perspectives on Einstein's E = mc²

Young Suh Kim, Marilyn E Noz

• Editorial: WSPC
• Año: 2018
• ISBN:
  9789813237728
• Categoría: Sciences physiques
• Categoría: Relativité en physique

Einstein's energy–momentum relation is applicable to particles of all speeds, including the particle at rest and the massless particle moving with the speed of light. If one formula or formalism is applicable to all speeds, we say it is "Lorentz-covariant." As for the internal space-time symmetries, there does not appear to be a clear way to approach this problem. For a particle at rest, there are three spin degrees of freedom. For a massless particle, there are helicity and gauge degrees of freedom. The aim of this book is to present one Lorentz-covariant picture of these two different space-time symmetries. Using the same mathematical tool, it is possible to give a Lorentz-covariant picture of Gell-Mann's quark model for the proton at rest and Feynman's parton model for the fast-moving proton. The mathematical formalism for these aspects of the Lorentz covariance is based on two-by-two matrices and harmonic oscillators which serve as two basic scientific languages for many different branches of physics. It is pointed out that the formalism presented in this book is applicable to various aspects of optical sciences of current interest.

Contents:

• Introduction
• Einstein's Philosophical Base
• More about Einstein
• Einstein in the United States
• Introduction to the Lorentz Group
• Wigner's Little Groups
• Lorentz completion of the Little Groups
• Lorentz-covariant Harmonic Oscillators
• Quarks and Partons
• Feynman's Rest of the Universe
• Further Applications of the Lorentz Group

Readership: College students with basic knowledge in physics and mathematics.
Key Features:

• Einstein's Lorentz covariance extended to internal space-time symmetries of elementary particles
• Concrete physical examples given to Wigner's subgroups of the Lorentz group
• Gell-Mann's quark model and Feynman's parton model as two limiting cases of one Lorentz-covariant entity, since Einstein's energy-momentum relations are applicable to both a massive particle at rest and a massless particle moving at the speed of light

Chapter 1

Introduction

When Einstein formulated his special relativity in 1905, he worked out the transformation law for point particles. The question is what happens when those particles have space–time extensions. The hydrogen atom is a case in point. The hydrogen atom is small enough to be regarded as a particle obeying Einstein’s law of Lorentz transformations including the energy–momentum relation

.

Yet, the hydrogen atom has a very rich internal space–time structure, rich enough to provide all the ingredients for quantum mechanics. Indeed, Niels Bohr was interested in why the energy levels of the hydrogen atom are discrete. His interest led to the replacement of the electron orbit by a standing wave.

Before and after 1927, Einstein and Bohr met occasionally to discuss physics. Einstein even stayed for an extended period at the Bohr Institute in Copenhagen, shown in Fig. 1.1.

It is possible that they discussed how the hydrogen atom with an electron orbit or as a standing wave looks to moving observers. However, there are no written records of their discussions. It is also possible that they never discussed this issue, since there were no hydrogen atoms moving with relativistic speeds, and/or since Einstein maintained a distance from the Copenhagen interpretation of quantum mechanics.

In either case, this is the issue to be resolved by the present generation of physicists. The present authors are not the first ones to raise this question. Among the many distinguished physicists who made laudable contributions to this fundamental problem, we should mention Paul A. M. Dirac (1902–1984) and Richard P. Feynman (1918–1988). They accepted the present form of quantum mechanics, and the Lorentz covariance on which Einstein’s special relativity is based.

Fig. 1.1.Niels Bohr Institute in Copenhagen. The plaque on the building says This building was the place where the foundations of atomic and modern physics were laid in a scientifically creative environment inspired by Niels Bohr in the 1920s and 1930s. The third floor of this building was used for hotel rooms for the visitors invited by Niels Bohr. Einstein was one of those visitors [Photos by Y. S. Kim (2015)].

In this book, we translate what they did into the mathematical language of Wigner’s little groups. Wigner in 1939 published a paper in the Annals of Mathematics (Wigner, 1939) discussing the subgroups of the Lorentz group whose transformations leave the momentum of a given particle invariant. These subgroups are called Wigner’s little groups. It is noted that some additional work is needed for this book to achieve contact with Dirac’s papers and Feynman’s papers and to make contact with the real world of physics.

In Secs. 1.1–1.3, we explain how the papers by Dirac, Feynman, and Wigner serve useful purposes for this book. In Sec. 1.4, we explain the scope of contents of the book.

Throughout this book, the concept of Lorentz covariance and the mathematics of Lorentz transformations constitute the basic scientific language. They will be discussed in detail in Chapter 5.

1.1Dirac’s Approach

We are all familiar with the Dirac equation. This equation is for spin-1/2 particles in the relativistic world. Its success in describing the electron–positron is well known. It also describes the Thomas effect in the spin–orbit coupling. It is known that Dirac was able to write his equation purely from mathematical considerations. He believed in mathematical beauty.

Dirac was the first one interested in the uncertainty relation between time and energy (Dirac, 1927). He noted that unlike the position and momentum variables, there are no quantum excitations. This was one of the difficulties in making quantum mechanics covariant in the Lorentzian world where the space and time variables become linearly mixed for moving observers.

Yet, Dirac never gave up his love for mathematical beauty. In 1945 (Dirac, 1945b), Dirac attempted to construct representations of the Lorentz group using harmonic oscillator wave functions. He had to start with the Gaussian form

However, he did not explain how the time variable is defined. Does this function mean the world becomes zero in the remote past or remote future?

In his paper of 1949 (Dirac, 1949) entitled Forms of Relativistic Dynamics, Dirac presented three possible ways to make quantum mechanics Lorentz-covariant. He introduces many fresh ideas, such as the instant form, light-cone coordinate system, and the Poincaré group as an extension of Heisenberg’s uncertainty relation. In this paper, Dirac mentions only difficulties, and makes no effort to provide resolutions.

In his paper of 1963 (Dirac, 1963), Dirac starts with two harmonic oscillators and exploits the symmetries contained in this dynamical system. He ends up with the symmetries of the group O(3, 2), namely, the Lorentz group with three spatial variables and two time variables. The harmonic oscillator is the language of quantum mechanics and the Lorentz group is the language of special relativity. Indeed, this paper tells us to construct a harmonic oscillator wave function which can be Lorentz-transformed.

1.2Feynman’s Approach

Richard Feynman made a giant step toward constructing Lorentz-covariant quantum mechanics. We are all familiar with Feynman diagrams. His diagrams serve as a tool for computing the scattering matrix or S-matrix applicable only to scattering processes. It was Feynman who realized this, and recommended harmonic oscillator wave functions for bound states in the Lorentz-covariant world (Feynman et al., 1971).

Earlier, in 1969 (Feynman, 1969a, b), Feynamn observed that the proton, when it moves with a velocity very close to that of light, appears like a collection of an infinite number of partons, unlike the bound state in the quark model (Gell-Mann, 1964). The proton is regarded as a quantum bound state of three quarks when it is at rest. We assume that the quantum mechanics applicable to this bound state is the same as that applicable to the hydrogen atom as a bound state of the proton and electron.

In his 1972 book on Statistical Mechanics (Feynman, 1998), when he introduces the density matrix, Feynman says:

When we solve a quantum-mechanical problem, what we really do is divide the universe into two parts — the system in which we are interested and the rest of the universe. We then usually act as if the system in which we are interested comprised the entire universe. To motivate the use of density matrices, let us see what happens when we include the part of the universe outside the system.

It is a challenge for us to find the rest of the universe in the Lorentz-covariant world. Is there a variable we do not measure in this Lorentz-covariant system?

Like Dirac, Feynman wrote many papers with the purpose of combining quantum mechanics with Einstein’s special relativity. However, his style of presentation is quite different from that of Dirac. We have listed their differences in Table 1.1. On the other hand, this table shows a possibility of combining their ideas for constructing a Lorentz-covariant form of quantum mechanics.

Table 1.1Dirac and Feynman.

	Paul A. M. Dirac	Richard P. Feynman
Means of expression	Poems	Diagrams cartoons
Personality	Seldom talks to anyone	Willing to join the crowd anywhere in the world
Primary interest	Standing waves Bound states	Running waves Scattering states
Favorite tools of research	Four-by-four matrices Harmonic oscillators	Path integrals Harmonic oscillators

Notes: Two different persons for the same purpose. They did not realize that their papers can be translated into the language of Wigner’s little groups which dictate the internal space-time symmetry of particles in the Lorentz–covariant world.

1.3Wigner’s Little Groups

In this book, we choose to achieve this goal by translating Dirac’s papers and Feynman’s papers to the mathematics of Eugene Wigner which dictates the internal space–time symmetries of particles in the Lorentz-covariant world.

As for Wigner’s mathematics, we are talking about his 1939 paper entitled Representations of the Inhomogeneous Lorentz Group published in Annals of Mathematics (Wigner, 1939). This paper also requires a translation. In this paper, Wigner constructed the subgroups of the Lorentz group whose transformations leave the momentum of a given particle invariant. These subgroups are called Wigner’s little groups. Fortunately, these little groups can be translated into the language of 2 × 2 matrices and harmonic oscillators.

Indeed, using matrix algebra, it is possible to derive the result given in the second row of Table 1.2. Using the oscillator representation, it is possible to derive the result given in the third row of the same table. A particle at rest can have three spin orientations. If it is Lorentz-boosted, the longitudinal component remains as the helicity. The transverse components collapse into one gauge degree of freedom.

For bound states, we believe that the same quantum mechanics is applicable to the hydrogen atom and to the proton in the quark model. While the hydrogen atom cannot be accelerated, modern accelerators routinely produce protons moving with speed very close to that of light. For these fast-moving protons, Feynman, in 1969, formulated his parton picture (Feynman, 1969a,b).

Table 1.2Further contents of Einstein’s E = mc².

Notes: The first row shows that Eins...