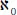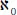Paradoxes in Mathematics

Stanley J. Farlow

• Editore: Dover Publications
• Anno: 2014
• ISBN:
  9780486791739
• Argomento: Mathematics
• Categoria: Games in Mathematics

There's more than one way to define a paradox, and this intriguing book offers examples of every kind. Stanley J. Farlow, a prominent educator and author, presents a captivating mix of mathematical paradoxes: the kind with surprising, nonintuitive outcomes; the variety that rely on mathematical sleight-of-hand to impress the unwary observer; and the baffling type with a solution that passes all understanding.
Students and puzzle enthusiasts will find plenty of thought-provoking enjoyment mixed with a bit of painless mathematical instruction among these twenty-eight conundrums. Some of them involve counting, some deal with infinity, and others draw on principles of geometry and arithmetic. None requires an extensive background in higher mathematics. Challenges include The Curve That Shook the World, a variation on the famous Monty Hall Problem, Space Travel in a Wineglass, Through Cantor's Looking Glass, and other fun-to-ponder paradoxes.

Through Cantor’s Looking Glass

It is not surprising that many paradoxes in mathematics involve the infinite, although since Cantor’s seminal research in the late 1800s, many of the old conundrums are now part of modern set theory and have long left the realm of the paradoxical. However, paradoxes still abound in the study of infinity, and for those not versed in Cantor’s basic theory of sets, working with infinite sets seems strange, to say the least. For that reason, we present a few of the enigmas and paradoxes of the past.

Throughout much of the history of mathematics, the subject of infinity has been taboo and belonged more in the realm of religion. The Greek philosopher Aristotle (circa 360–280 B.C.), one of the first mathematicians to think about the subject, felt there were two varieties of infinity, the potential and the actual. He said the natural numbers 1, 2, 3, ... are potentially infinite since they go on forever and have no greatest number. He felt they were not actually infinite in size since they were not a completed entity.

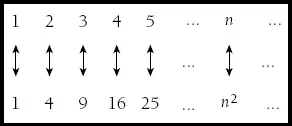
In the 1600s, the Italian scientist, mathematician, and astronomer Galileo made an interesting observation about the natural numbers 1,2,3,… when he subdivided them into two types: the perfect squares: 1, 4, 9, 16, 25, … or numbers that are squares of other numbers. Since the perfect squares are a subset or subcollection of all natural numbers 1,2,3,… that would seem like there are fewer of them, as illustrated in Figure 1.

More natural numbers than perfect squares

Figure 1

However, as Galileo observed, if you line up the perfect squares as Figure 2 shows, you can match any perfect square with a natural number, and any natural number with a perfect square, suggesting the two sets have the same number of members.

Just as many perfect squares as natural numbers

Figure 2

Galileo’s conclusion was that when it comes to infinite sets, things are not the same as for finite sets.

The Godfather of Infinity: Georg Cantor: The subject of infinity as we know it today had its origins in the work of the German mathematician. Georg Cantor (1845–1918), whose groundbreaking insights rest upon a very simple idea (as do many seminal insights). Suppose you are unable to count and would like to know if your hands have the same number of fingers.

Georg Cantor

Not being able to count, you do something more basic. You simply place the thumb of one hand against the thumb of your other hand, then place your index finger of one hand against the index finger of your other hand, and do the same for the remaining fingers. When you are finished, your fingers are all matched up in a one-to-one correspondence: every finger on each hand has exactly one kindred soul on the other. You may not know how many fingers you have on each hand, but you know they are the same.

Now, what if you had an infinite number of fingers? In this case, it doesn’t matter if you can’t count, no one else can either. I mean, no one can count that high! Cantor’s inspiration was that, even if we can’t count infinite sets, we can tell if they have the same number of members by applying the “finger rule” used when determining that our hands had the same number of fingers.

Cantor called the size of a set the cardinality of the set, and if a set can be placed in a one-to-one correspondence with the natural numbers 1,2,3,… the “size” of the set is called countably infinite, and these types of sets are said to have cardinality

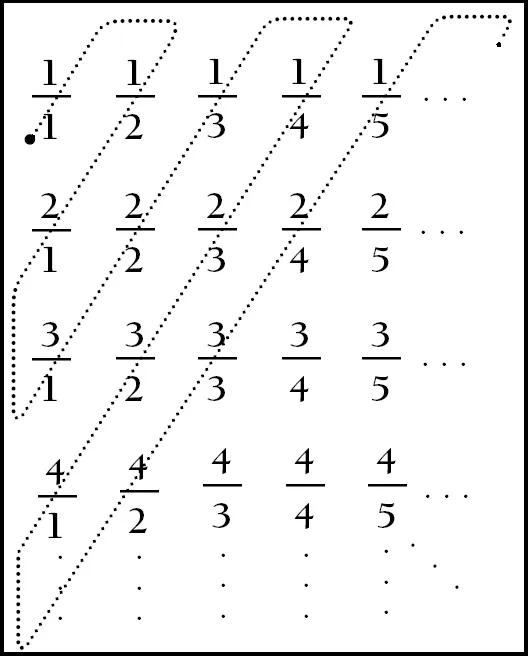
(aleph- null).¹

Cantor then asked if all infinite sets have the same cardinality; that is, are there larger infinities? The next infinite set Cantor tested was the rational numbers (ratios of natural numbers), and if you were a guessing person you might be tempted to say there are “more” rational numbers than integers since the natural numbers are a subset of the rational numbers. If you did, however, you would be wrong since Cantor found an ingenious matchup (like the finger matching, but with more fingers) between the natural numbers 1,2,3,… and all the positive rational numbers illustrated in Figure 3.

Finger matching between 1,2,3,... and the positive fractions

Figure 3

If the table in Figure 3 were continued indefinitely downward and to the right, it would contain all the rational numbers 1, ½, ⅛, … (with many duplications, such as 2/2 and 3/3, 1/3 and 3/9, and so on), Hence, Cantor concluded natural numbers and rational numbers each had the same number of elements.² In other words, each had cardinality

. Like we said, things get strange in Cantor’s world of infinity.

Larger Infinities? Cantor then looked around for sets that might have “more” members, the most obvious set to try being the real numbers. The answer was astounding. Cantor proved that there are “more” real numbers than natural numbers: 1,2,3,…, that it is impossible to match up the real numbers with the natural numbers, and that since the natural numbers are a subset of the real numbers, the cardinality of the real numbers must be larger than that of the natural numbers. So how did Cantor do this?

Proofs that show something cannot happen are often proved by what is called proof by contradiction, where one assumes the contrary, that it can happen. In this case, we assume the rational numbers and the real numbers between 0 and 1 can be matched up in a one-to-one manner, and then arrive at some type of contradiction, from which our conclusion is there is no correspondence between the rational numbers and these real numbers.

Cantor used an ingenious proof called the diagonalization process, where he hypothesized that it was possible to match up the natural numbers with all positive real numbers. A typical matching is shown in Figure 4 where the natural numbers 1,2,3,… are in the left column, and typical real numbers, expressed in decimal form, on the right.

Cantor’s hypothesized one-to-one correspondence b...