The Britannica Guide to Geometry

Britannica Educational Publishing, William Hosch

• Editore: Britannica Educational Publishing
• Anno: 2010
• ISBN:
  9781615302178
• Argomento: Mathematik
• Categoria: Geometrie

More than a study of shapes and angles, geometry reflects an amalgamation of discoveries over time. This book not only provides readers with a comprehensive understanding of geometric shapes, axioms, and formulas, it presents the field's brilliant minds—from Euclid to Wendelin Werner and many in between—whose works reflect a progression of mathematical thought throughout the centuries and have helped produce the various branches of geometry as they are known today. Detailed diagrams illustrate various concepts and help make geometry accessible to all.

CHAPTER 1
HISTORY OF GEOMETRY

The earliest known unambiguous examples of written records—dating from Egypt and Mesopotamia about 3100 BCE—demonstrate that ancient peoples had already begun to devise mathematical rules and techniques useful for surveying land areas, constructing buildings, and measuring storage containers. Beginning about the 6th century BCE, the Greeks gathered and extended this practical knowledge and from it generalized the abstract subject now known as geometry, from the combination of the Greek words geo (“Earth”) and metron (“measure”) for the measurement of the Earth.

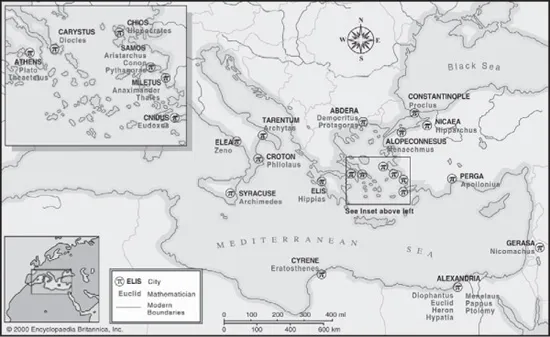
This map spans a millennium of prominent Greco-Roman mathematicians, from Thales of Miletus (c. 600 BCE) to Hypatia of Alexandria (c. 400 CE). Their names are located on the map under their cities of birth.

ANCIENT GEOMETRY: PRACTICAL AND EMPIRICAL

---

The origin of geometry lies in the concerns of everyday life. The traditional account, preserved in Herodotus’s History (5th century BCE), credits the Egyptians with inventing surveying in order to reestablish property values after the annual flood of the Nile. Similarly, eagerness to know the volumes of solid figures derived from the need to evaluate tribute, store oil and grain, and build dams and pyramids. Even the three abstruse geometrical problems of ancient times—to double a cube, trisect an angle, and square a circle, all of which will be discussed later—probably arose from practical matters, from religious ritual, timekeeping, and construction, respectively, in pre-Greek societies of the Mediterranean. And the main subject of later Greek geometry, the theory of conic sections, owed its general importance, and perhaps also its origin, to its application to optics and astronomy.

While many ancient individuals, known and unknown, contributed to the subject, none equaled the impact of Euclid and his Elements, a book on geometry now 2,300 years old and the object of as much painful and painstaking study as the Bible. Much less is known about Euclid, however, than about Moses. In fact, the only thing known with a fair degree of confidence is that Euclid taught at the Library of Alexandria during the reign of Ptolemy I (323–285/283 BCE). Euclid wrote not only on geometry but also on astronomy and optics and perhaps also on mechanics and music. Only the Elements, which was extensively copied and translated, has survived intact.

Euclid’s Elements was so complete and clearly written that it literally obliterated the work of his predecessors. What is known about Greek geometry before him comes primarily from bits quoted by Plato and Aristotle and by later mathematicians and commentators. Among other precious items they preserved are some results and the general approach of Pythagoras (c. 580–c. 500 BCE) and his followers. The Pythagoreans convinced themselves that all things are, or owe their relationships to, numbers. The doctrine gave mathematics supreme importance in the investigation and understanding of the world. Plato developed a similar view, and philosophers influenced by Pythagoras or Plato often wrote ecstatically about geometry as the key to the interpretation of the universe. Thus ancient geometry gained an association with the sublime to complement its earthy origins and its reputation as the exemplar of precise reasoning.

FINDING THE RIGHT ANGLE

Ancient builders and surveyors needed to be able to construct right angles in the field on demand. The method employed by the Egyptians earned them the name “rope pullers” in Greece, apparently because they employed a rope for laying out their construction guidelines. One way that they could have employed a rope to construct right triangles was to mark a looped rope with knots so that, when held at the knots and pulled tight, the rope must form a right triangle. The simplest way to perform the trick is to take a rope that is 12 units long, make a knot 3 units from one end and another 5 units from the other end, and then knot the ends together to form a loop. However, the Egyptian scribes have not left us instructions about these procedures, much less any hint that they knew how to generalize them to obtain the Pythagorean theorem: the square on the line opposite the right angle equals the sum of the squares on the other two sides. Similarly, the Vedic scriptures of ancient India contain sections called sulvasutras, or “rules of the rope,” for the exact positioning of sacrificial altars. The required right angles were made by ropes marked to give the triads (3, 4, 5) and (5, 12, 13).

In Babylonian clay tablets (c. 1700–1500 BCE) modern historians have discovered problems whose solutions indicate that the Pythagorean theorem and some special triads were known more than 1000 before Euclid. A right triangle made at random, however, is very unlikely to have all its sides measurable by the same unit—that is, every side a whole-number multiple of some common unit of measurement. This fact, which came as a shock when discovered by the Pythagoreans, gave rise to the concept and theory of incommensurability.

LOCATING THE INACCESSIBLE

By ancient tradition, Thales of Miletus, who lived before Pythagoras in the 6th century BCE, invented a way to measure inaccessible heights, such as the Egyptian pyramids. Although none of his writings survives, Thales may well have known about a Babylonian observation that for similar triangles (triangles having the same shape but not necessarily the same size) the length of each corresponding side is increased (or decreased) by the same multiple. The ancient Chinese arrived at measures of inaccessible heights and distances by another route, using “complementary” rectangles, which can be shown to give results equivalent to those of the Greek method involving triangles.

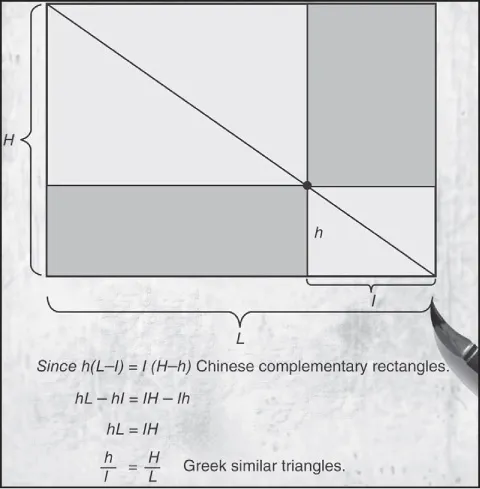
The figure illustrates the equivalence of the Chinese complementary rectangles theorem and the Greek similar triangles theorem. Encyclopædia Britannica, Inc.

ESTIMATING THE WEALTH

A Babylonian cuneiform tablet written some 3,500 years ago treats problems about dams, wells, water clocks, and excavations. It also has an exercise on circular enclosures with an implied value of π = 3. The contractor for King Solomon’s swimming pool, who made a pond 10 cubits across and 30 cubits around (1 Kings 7:23), used the same value. However, the Hebrews should have taken their π from the Egyptians before crossing the Red Sea, for the Rhind papyrus (c. 2000 BCE; our principal source for ancient Egyptian mathematics) implies π = 3.1605.

Knowledge of the area of a circle was of practical value to the officials who kept track of the pharaoh’s tribute as well as to the builders of altars and swimming pools. Ahmes, the scribe who copied and annotated the Rhind papyrus (c. 1650 BCE), has much to say about cylindrical granaries and pyramids, whole and truncated. He could calculate their volumes, and, as appears from his taking the Egyptian seked, the horizontal distance associated with a vertical rise of one cubit, as the defining quantity for the pyramid’s slope, he knew something about similar triangles.

ANCIENT GEOMETRY: ABSTRACT AND APPLIED

---

THE THREE CLASSICAL PROBLEMS

In addition to proving mathematical theorems, ancient mathematicians constructed various geometrical objects. Euclid arbitrarily restricted the tools of construction to a straightedge (an unmarked ruler) and a compass. The restriction made three problems of particular interest (to double a cube, to trisect an arbitrary angle, and to square a circle) very difficult—in fact, impossible. Various methods of construction using other means were devised in the classical period, and efforts, always unsuccessful, using a straightedge and a compass persisted for the next 2,000 years. In 1837 the French mathematician Pierre Laurent Wantzel proved that doubling the cube and trisecting the angle are impossible, and in 1880 the German mathematician Ferdinand von Lindemann showed that squaring the circle is impossible, as a consequence of his proof that π is a transcendental number.

DOUBLING THE CUBE

The Vedic scriptures made the cube the most advisable form of altar for anyone who wanted to supplicate in the same place twice. The rules of ritual required that the altar for the second plea have the same shape but twice the volume of the first. If the sides of the original and derived altars are a and b, respectively, then b ³ = 2a³. The problem came to the Greeks together with its ceremonial content. An oracle disclosed that the citizens of Delos could free themselves of a plague merely by replacing an existing altar by one twice its size. The Delians applied to Plato. He replied that the oracle did not mean that the gods wanted a larger altar but that they had intended “to shame the Greeks for their neglect of mathematics and their contempt for geometry.” With this blend of Vedic practice, Greek myth, and academic manipulation, the problem of the duplication of the cube took a leading place in the formation of Greek geometry.

Hippocrates of Chios, who wrote an early Elements about 450 BCE, took the first steps in cracking the altar problem. He reduced the duplication to finding two mean proportionals between 1 and 2—that is, to finding lines x and y in the ratio 1:x = x:y = y:2. After the intervention of the Delian oracle, several geometers around Plato’s Academy found complicated ways of generating mean proportionals.

A few generations later, Eratosthenes of Cyrene (c. 276–c. 194 BCE) devised a simple instrument with moving parts that could produce approximate mean proportionals.

TRISECTING THE ANGLE

The Egyptians told time at night by the rising of 12 asterisms (constellations), each requiring on average two hours to rise. In order to obtain more convenient intervals, the Egyptians subdivided each of their asterisms into three parts, or decans. That presented the problem of trisection. It is not known whether the second celebrated problem of archaic Greek geometry, the trisection of any given angle, arose from the difficulty of the decan, but it is likely that it came from some problem in angular measure.

Several geometers of Plato’s time tried their hands at trisection. Although no one succeeded in finding a solution with a straightedge and a compass, they did succeed with a mechanical device and by a trick. The mechanical device, perhaps never built, creates what the ancient geometers called a quadratrix. Invented by a geometer known as Hippias of Elis (fl. 5th century BCE), the quadratrix is a curve traced by the point of intersection between two moving lines, one rotating uniformly through a right angle, the other gliding uniformly parallel to itself.

The trick for trisection is an application of what the Greeks called neusis, a maneuvering of a measured length into a special position to complete a geometrical figure. A late version of its use, ascribed to Archimedes (c. 285–212/211 BCE), exemplifies the method of angle trisection.

SQUARING THE CIRCLE

The pre-Euclidean Greek geometers transformed the practical problem of determining the area of a circle into a tool of discovery. Three approaches can be distinguished: Hippocrates’ dodge of substituting one problem for another; the application of a mechanical instrument, as in Hippias’ device for trisecting the angle; and the technique that proved the most fruitful, the closer and closer approximation to an unknown magnitude difficult to study (e.g., the area of a circle) by a series of known magnitudes easier to study (e.g., areas of polygons)—a technique known in modern times as the “method of exhaustion” and attributed by its greatest practitioner, Archimedes, to Plato’s student Eudoxus of Cnidus (c. 408–c. 355 BCE).

While not able to square the circle, Hippocrates did demonstrate the quadratures of lunes. That is, he showed that the area between two intersecting circular arcs could be expressed exactly as a rectilinear area and so raised the expectation that the circle itself could be treated similarly. A contemporary of Hippias’ discovered that the quadratrix could be used to almost rectify circles. These were the substitution and mechanical approaches.

The method of exhaustion as developed by Eudoxus approximates a curve or surface by using polygons with calculable perimeters and areas. As the number of sides of a regular polygon inscribed in a circle increases indefinitely, its perimeter and area “exhaust,” or take up, the circumference and area of the circle to within any assignable error of length or area, however small. In Archimedes’ usage, the method of exhaustion produced upper and lower bounds for the value of π, the ratio of any circle’s circumference to its diameter. This he accomplished by inscribing a polygon within a circle, and circumscribing a polygon around it as well, thereby bounding the circle’s circumference between the polygons’ calculable perimeters. He used polygons with 96 sides and thus bound π between 3 ¹⁰/₇₁ and 3 ¹/₇.

IDEALIZATION AND PROOF

The last great Platonist and Euclidean commentator of antiquity, Proclus (c. 410–485 CE), attributed to the inexhaustible Thales the discovery of the far-from-obvious proposition that even apparently obvious propositions need proof. Proclus referred especially to the theorem, known in the Middle Ages as the Bridge of Asses, that in an isosceles triangle the angles opposite the equal sides are equal. The theorem may have earned its nickname from the Euclidean figure or from the commonsense notion that only an ass would require proof of so obvious a statement.

The ancient Greek geometers soon followed Thales over the Bridge of Asses. In the 5th century BCE the philosopher-mathematician Democritus (c. 460–c. 370 BCE) declared that his geometry excelled all the knowledge of the Egyptian rope pullers because he could prove what he claimed. By the time of Plato, geometers customarily proved their propositions. Their compulsion and the multiplication of theorems it produced fit perfectly with the endless questioning of Socrates and the uncompromising logic of Aristotle. Perhaps the origin, and certainly the exercise, of the peculiarly Greek method of mathematical proof should be sought in the same social setting that gave rise to the practice of philosophy—that is, the Greek polis. There citizens learned the skills of a governing class, and the wealthier among them enjoyed the leisure to engage their minds as they pleased, however useless the result, while slaves attended to the necessities of life. Greek society could support the transformation of geometry from a practical art to a deductive science. Despite its rigour, however, Greek geometry does not satisfy the demands of the modern systematist. Euclid himself sometimes appeals to inferences drawn from an intuitive grasp of concepts such as point an...

Indice dei contenuti

• Cover Page
• Title Page
• Copyright Page
• Contents
• Introduction
• Chapter 1: History of Geometry
• Chapter 2: Branches of Geometry
• Chapter 3: Biographies
• Appendix of Geometric Terms and Concepts
• Glossary
• Bibliography
• Index