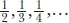Circularity

A Common Secret to Paradoxes, Scientific Revolutions and Humor

Ron Aharoni

• Editore: WSPC
• Anno: 2016
• ISBN:
  9789814723701
• Argomento: Mathematik
• Categoria: Angewandte Mathematik

"Circularity" is the story of a Janus-faced conceptual structure, that on the one hand led to deep scientific discoveries, and on the other hand is used to trick the mind into believing the impossible. Alongside mathematical revolutions that eventually led to the invention of the computer, the book describes ancient paradoxes that arise from circular thinking. Another aspect of circularity, its ability to entertain, leads to a surprising insight on the time old question "What is humor".Contents:The Protagonist of the StoryA Nation Enamored with ParadoxesFrom Proof to ParadoxFrom Paradox to ProofThe Paradoxes of the Direction of TimeThe Paradox of All Paradoxes — the Mind-Body ProblemReadership: Researchers in mathematics, philosophy and general public.Paradoxes; Circularity; Mathematical Logic; Godel; Turing; Free Will; Mind-Body Key Features:It represents the Godel theory in a clear yet rigorous wayIt studies paradoxes in a unified way — unifying the so-called "logical paradoxes" and the philosophical paradoxesIt is a popular introduction to set theory

The Illuminated Side — Scientific Breakthroughs

Part IV: Large Infinities and Still Larger Ones

Infinity is the place where things happen that don’t.

(Anonymous student)

You Shall See the Land from Afar

So far we have met circularity from its inimical side, that which confuses people and diverts them from the straight and narrow. But just as historical figures have many personae (what was Napoleon — a big criminal or a great man?) so does circularity have another facet, which has proved of great value to science. It emerges when phenomena of circularity are unveiled, usually thereby supplying proof to the impossibility of some task. In the final analysis, the scales weighing the virtue and vice of circularity would tilt towards the illuminated side. Going around in circles means not progressing, and therefore the dark side of circularity hasn’t changed much in the last two millennia. The illuminated side, on the other hand, has partaken in the progress of scientific activity.

In this part we shall meet one discovery based on circularity, a mathematical theory developed by the German mathematician Georg Cantor (1845–1918). Cantor worked in the northern German town of Halle, whose main claim to fame is as the birth place of another Georg — the composer Georg Friedrich Handel. Cantor used a circularity argument to prove a “non-existence” result — that of the largest set in the world. It does not exist. Every set has one larger than it.

A profound discovery entitles the discoverer to a place in the scientific pantheon, and Cantor did indeed win this well-deserved glory, unfortunately mainly posthumously. In his lifetime the discovery brought him mainly heartbreak. When he set on his trail of research he sought neither the glory nor the struggle attending the discovery. Having started his career in a classical area that deals with the shape of waves, he had made his discovery almost against his will. At some point in his research he noticed a surprising fact that ultimately proved much more important than the original line of research: that there is more than one type of infinity. There are large infinities and there are still larger ones.

Until Cantor’s time mathematicians distinguished between finite sets, that are “small” (compared to infinity), and infinite sets, that are “large”. Of course not all finite sets are equal in size. A set of 3 is larger than a set of 2. But with regard to infinite sets it was assumed that such a distinction does not apply, that they are all “large” and that’s it. Cantor discovered that in the kingdom of infinite sets there are subtleties too, and that just as a finite set can be larger than another so can an infinite set be larger than another.

This insight generated a new field — set theory, which investigates some of the most fundamental mathematical concepts. So much so, that today set theory is taught in most universities in first year. Cantor’s bad luck was his timing. He made his discovery precisely when other mathematicians reached conclusions that at least superficially appeared to be contrary to his own. Cantor spoke of infinity as an existing entity at a time his colleagues referred to it disrespectfully as “actual infinity”, arguing that there is no real infinity. Infinity is not achieved, it can only be approached by numbers that are larger and larger.

It all began when the 19^th century mathematicians tried to put some order in a field that was already two hundred years old then: differential and integral calculus (often called just “calculus”). This is the mathematical field that studies change, such as we find in motion — the change of place over time. You may wonder — isn’t motion studied in elementary school? “Car A goes at a speed of 50 kilometers an hour. If car B leaves from the same spot an hour later, at a speed of 100 kilometers an hour, in the same direction, when will it catch up?” The point is that in elementary school cars go at constant speed. In real life this rarely happens. Bodies change their speed. So, to measure speed it does not suffice to say “the speed of a car travelling 100 kilometers in 2 hours is 50 kilometers an hour.” You’d then be speaking of its average speed. To calculate the real speed (even to define what it is) you need to measure motion over smaller and smaller time intervals. The smaller the interval, the more accurate is the approximation of the real speed. In other words, you should look at time intervals that tend to zero.

The mathematicians of the 17^th and 18^th centuries spoke of “infinitely small intervals”, a term they never entirely clarified. In the 19^th century it became clear that such fuzzy concepts cannot be used for rigorous proofs. There is no such thing as an “infinitely small” quantity. Instead, another notion was invented: “as small as we please”. Instead of one “infinitely small” number they spoke of a sequence of numbers that goes to zero. For example, the sequence

tends to 0, meaning that its terms get as close to zero as we wish.

Similarly, on the other side of the spectrum, where numbers were until then “infinitely large”, they became “numbers as large as we please”. For example, in the sequence 1, 2, 3, … the numbers get as large as we wish. Do you want the terms to be larger than a million? No problem: as from the million and one place all terms are larger than a million. In this formulation there is no actual infinity. “… Thou shalt see the land before thee; but thou shalt not go thither,” as God told Moses when he approached the land of Canaan (Deuteronomy, 32:52).

In Cantor’s world the Promised Land is reached. He speaks of sets that are truly infinite. This obviously aroused strong resistance. To rock the foundations of mathematics that have been so recently and so painstakingly erected, and to reinstate within the fort the newly exorcised demon of actual infinity, was heresy or worse — lack of understanding. Henri Poincaré, a leading mathematician of the time, called set theory “a childhood disease from which mathematics will recover in due course”. Cantor’s most bitter enemy was Leopold Kronecker, an influential member of the German academy. Kronecker called him a “mathematical charlatan”, maintained that “there may be philosophy or theology in Cantor’s work, but certainly no mathematics”, and accused him of corrupting the youth, the charge for which Socrates paid with his life some 2300 years earlier. As a result Cantor failed to get a much desired university position in one of the leading universities. This and the tragic loss of a son in 1899 aggravated a depressive illness from which he suffered, and he ended his life in a mental asylum.

What is “Counting”

Count them.
You can count them. They
Are not like the sand on the seashore. They
Are not innumerable like the stars. They are like lonely people
On the corner or in the street.

(Yehuda Amichai, In the Full Severity of Mercy, 1^st stanza)

“The size of an infinite set” is seemingly a complex notion. By contrast, “the size of a finite set” is simple: isn’t it just the number of its elements? In fact it is not simple at all. Have you ever contemplated the question of what is a number? This is such a basic notion that we never stop to examine it. As far as we are concerned, a set of three apples comes to the world complete with the label “3”. Well, not quite. Numbers are a tool invented by man, one of his most sophisticated.

To understand the wisdom of numbers, think of a person who wishes to compare the height of two tables in his apartment: the dining table and his desk. One way to do it is to haul the table from the study to the kitchen (or vice versa), stand them side by side and find which is higher. A simpler way is to take a stick, mark on it the height of the desk, carry the stick to the kitchen, and compare the height of the notch with the height of the dining table.

Numbers are such a “stick”. In order to know if a zoo population comprises more giraffes or more elephants, we do not need to put them side by side. Instead, we can employ as a “measuring yard” a standard set — that of the numbers 0, 1, 2, 3, … . Like the stick, this is a mediator. Counting the elephants means assigning to each an element from this set, in order. We then proceed to the giraffes’ compound, count them, and measure on the “stick” of numbers which notch is higher. This stick is even better than the material one, because it can be carried in the head.

It is quite incredible, but for many tens of millennia nobody stopped to wonder what they are doing when they count. For Cantor, wishing as he did to measure infinite sets, this was an insight he could not go without. In the infinite case, the direct method (i.e. without the mediation of numbers) is the only way. Ordinary numbers are far behind us and “infinity” is not a number. Hence, in order to compare infinite sets, we must “put them one against the other”, namely establish direct correspondence. This was the crucial observation that led Cantor to his discoveries. The following is what defines two sets as equal in size:

Two sets have equal size if they can be matched, one element of the first against each element of the second.

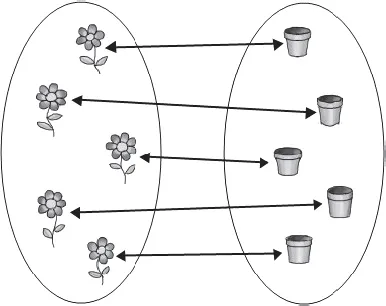
For example, if you want to show that both your hands take pride in the same number of fingers (if luckily this is the case) you do not need the mediation of the set of numbers {1, 2, 3, 4, 5}. You can simply put your hands one against the other, finger against finger, thereby forming a one-to-one correspondence. The arrows in the following diagram show that the set of flowers is equal in size to the set of pots.

A Surprise

You don’t understand mathematics. You just get used to it.

(John von Neumann, mathematician)

What are there more of in the world — humans or women? Humans of course. After all, women are only part of humanity. There are also men. The set of women is just part of the set of all human beings, and so it is smaller. There are about twice as many humans as women.

What are there more of in the world, natural numbers or even numbers? Natural numbers of course. After all, even numbers are only part of all numbers. There are also odd numbers. The set of even numbers is just a part of the set of all numbers, and so it is smaller. There are twice as many natural numbers as even numbers.

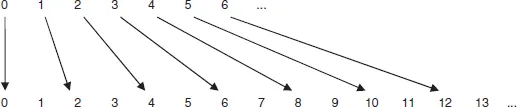
True, or not? Only partially. Indeed, there are twice as many natural numbers as even numbers, but in the infinite case “twice as many” doesn’t mean “more than”. Surprisingly, the two sets are equal in size. This can be shown by matching, just as you can show that both your hands have the same number of digits, by putting them one against the other. We can assign to every natural number an even number, in the following way. To zero we assign 0; to 1 we assign 2; to 3 we assign 6, and so on: to every number we assign the number multiplied by 2. This forms a matching in which to every number an even number is assigned, and every even number is assigned to precisely one number — half of itself. The matching is depicted in the following diagram:

I deliberately listed the odd numbers as well (bottom row), so that it is clear that the top set is matched to what is only a partial set of itself.

The story of Tristram Shandy, the protagonist of Laurence Sterne’s book, The Life and Opinions of Tristram Shandy, Gentleman, illustrates this principle. Shandy is busy writing his autobiography. He is so fastidious, that it takes him a hundred days to describe each day of his life (in the book it is a bit different, but this is the idea). Will he ever complete his task? If his lifespan is finite then of course not, but if he lives forever he will. For example, on the 100,000^th day of writing he will be recording the 1000^th day of his life. Tristram Shandy has one more reason to wish to live forever than the rest of us.

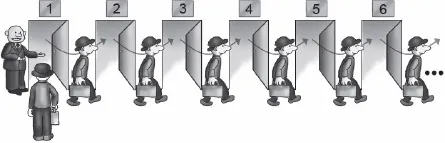
Cantor’s set theory had a guardian angel in the form of David Hilbert (1862–1943), the most prominent mathematician of the late 19^th and early 20^th centuries. He fell in love with the new theory and became its proponent. “From the paradise that Cantor created for us nobody can expel us,” he said. One of his contributions was a story illustrating the special features of the concept of infinity. The hero of the story is the owner of a hotel, somewhere in heaven (perhaps in Cantor’s paradise), that has infinitely many rooms, numbered 1, 2, 3, … . One day the hotel was full to capacity, occupied to its last room (well, it doesn’t really have a last room). And then, in the evening, another guest came, gasping for breath. Had the hotel been finite he would have had to sleep at large. Not so in an infinite hotel. The manager used an infinitely powerful loudspeaker to ask his guests each to move to the next room. So, the guest in room number 1 moved to room number 2, the guest in room number 2 to room number 3 and so forth. Every guest again had his own room, and one room had become vacant — room number 1, to house the new guest.

Then, again, by the evening of the next day all rooms were occupied, when something even more disastrous happened: suddenly infinitely many new guests arrived. Again the manager did not lose his presence of mind. He told every guest to move to the room bearing the number double to his present one. Namely, the guest in room number 1 moved to room number 2, the guest in room number 2 to room number 4, the guest in room number 3 to room number 6 and so on. Every guest had a room of his own and infinitely many rooms were vacated: all the odd-numbered ones. Room was found for the infinitely many newcom...

Indice dei contenuti

• Cover
• Halftitle
• Title
• Copyright
• Cats and Tails
• Acknowledgments
• Contents
• The Dark Side — Paradoxes
• The Illuminated Side — Scientific Breakthroughs
• Bibliography