An Introduction to Science and Technology Studies

Sergio Sismondo

• Publisher: Wiley-Blackwell
• Year: 2011
• ISBN:
  9781444358889
• Edition: 2
• Topic: Philosophie
• Subtopic: Philosophie et éthique en sciences

An Introduction to Science and Technology Studies, Second Edition reflects the latest advances in the field while continuing to provide students with a road map to the complex interdisciplinary terrain of science and technology studies.

• Distinctive in its attention to both the underlying philosophical and sociological aspects of science and technology
• Explores core topics such as realism and social construction, discourse and rhetoric, objectivity, and the public understanding of science
• Includes numerous empirical studies and illustrative examples to elucidate the topics discussed
• Now includes new material on political economies of scientific and technological knowledge, and democratizing technical decisions
• Other features of the new edition include improved readability, updated references, chapter reorganization, and more material on medicine and technology

1

The Prehistory of Science and Technology Studies

A View of Science

Let us start with a common picture of science. It is a picture that coincides more or less with where studies of science stood some 50 years ago, that still dominates popular understandings of science, and even serves as something like a mythic framework for scientists themselves. It is not perfectly uniform, but instead includes a number of distinct elements and some healthy debates. It can, however, serve as an excellent foil for the discussions that follow. At the margins of science, and discussed in the next section, is technology, typically seen as simply the application of science.

In this picture, science is a formal activity that creates and accumulates knowledge by directly confronting the natural world. That is, science makes progress because of its systematic method, and because that method allows the natural world to play a role in the evaluation of theories. While the scientific method may be somewhat flexible and broad, and therefore may not level all differences, it appears to have a certain consistency: different scientists should perform an experiment similarly; scientists should be able to agree on important questions and considerations; and most importantly, different scientists considering the same evidence should accept and reject the same hypotheses. The result is that scientists can agree on truths about the natural world.

Within this snapshot, exactly how science is a formal activity is open. It is worth taking a closer look at some of the prominent views. We can start with philosophy of science. Two important philosophical approaches within the study of science have been logical positivism, initially associated with the Vienna Circle, and fa-lsificationism, associated with Karl Popper. The Vienna Circle was a group of prominent philosophers and scientists who met in the early 1930s. The project of the Vienna Circle was to develop a philosophical understanding of science that would allow for an expansion of the scientific worldview - particularly into the social sciences and into philosophy itself. That project was immensely successful, because positivism was widely absorbed by scientists and non-scientists interested in increasing the rigor of their work. Interesting conceptual problems, however, caused positivism to become increasingly focused on issues within the philosophy of science, losing sight of the more general project with which the movement began (see Friedman 1999; Richardson 1998).

Logical positivists maintain that the meaning of a scientific theory (and anything else) is exhausted by empirical and logical considerations of what would verify or falsify it. A scientific theory, then, is a condensed summary of possible observations. This is one way in which science can be seen as a formal activity: scientific theories are built up by the logical manipulation of observations (e.g. Ayer 1952 [1936]; Carnap 1952 [1928]), and scientific progress consists in increasing the correctness, number, and range of potential observations that its theories indicate.

For logical positivists, theories develop through a method that transforms individual data points into general statements. The process of creating scientific theories is therefore an inductive one. As a result, positivists tried to develop a logic of science that would make solid the inductive process of moving from individual facts to general claims. For example, scientists might be seen as creating frameworks in which it is possible to uniquely generalize from data (see Box 1.1).

Positivism has immediate problems. First, if meanings are reduced to observations, there are many “synonyms,” in the form of theories or statements that look as though they should have very different meanings but do not make different predictions. For example, Copernican astronomy was initially designed to duplicate the (mostly successful) predictions of the earlier Ptolemaic system; in terms of observations, then, the two systems were roughly equivalent, but they clearly meant very different things, since one put the Earth in the center of the universe, and the other had the Earth spinning around the Sun. Second, many apparently meaningful claims are not systematically related to observations, because theories are often too abstract to be immediately cashed out in terms of data. Yet surely abstraction does not render a theory meaningless. Despite these problems and others, the positivist view of meaning taps into deep intuitions, and cannot be entirely dismissed.

Even if one does not believe positivism’s ideas about meaning, many people are attracted to the strict relationship that it posits between theories and observations. Even if theories are not mere summaries of observations, they should be absolutely supported by them. The justification we have for believing a scientific theory is based on that theory’s solid connectionto data. Another view, then, that is more loosely positivist, is that one can by purely logical means make predictions of observations from scientific theories, and that the best theories are ones that make all the right predictions. This view is perhaps best articulated as falsificationism, a position developed by (Sir) Karl Popper (e.g. 1963), a philosopher who was once on the edges of the Vienna Circle.

Box 1.1 The problem of induction

Among the asides inserted into the next few chapters are a number of versions of the “problem of induction.” These are valuable background for a number of issues in Science and Technology Studies (STS). At least as stated here, these are theoretical problems that only occasionally become practical ones in scientific and technical contexts. While they could be paralyzing in principle, in practice they do not come up. One aspect of their importance, then, is in finding out how scientists and engineers contain these problems, and when they fail at that, how they deal with them.

The problem of induction arose with David Hume’s general questions about evidence in the eighteenth century. Unlike classical skeptics, Hume was interested not in challenging particular patterns of argument, but in showing the fallibility of arguments from experience in general. In the sense of Hume’s problem, induction extends data to cover new cases. To take a standard example, “the sun rises every 24 hours” is a claim supposedly established by induction over many instances, as each passing day has added another data point to the overwhelming evidence for it. Inductive arguments take n cases, and extend the pattern to the n+1st. But, says Hume, why should we believe this pattern? Could the n+1st case be different, no matter how large n is? It does no good to appeal to the regularity of nature, because the regularity of nature is at issue. Moreover, as Ludwig Wittgenstein (1958) and Nelson Goodman (1983 [1954]) show, nature could be perfectly regular and we would still have a problem of induction. This is because there are many possible ideas of what it would mean for the n+1st case to be the same as the first n. Sameness is not a fully defined concept.

It is intuitively obvious that the problem of induction is insoluble. It is more difficult to explain why, but Karl Popper, the political philosopher and philosopher of science, makes a straightforward case that it is. The problem is insoluble, according to him, because there is no principle of induction that is true. That is, there is no way of assuredly going from a finite number of cases to a true general statement about all the relevant cases. To see this, we need only look at examples. “The sun rises every 24 hours” is false, says Popper, as formulated and normally understood, because in Polar regions there are days in the year when the sun never rises, and days in the year when it never sets. Even cases taken as examples of straightforward and solid inductive inferences can be shown to be wrong, so why should we be at all confident of more complex cases?

For Popper, the key task of philosophy of science is to provide a demarcation criterion, a rule that would allow a line to be drawn between science and non-science. This he finds in a simple idea: genuine scientific theories are falsifiable, making risky predictions. The scientific attitude demands that if a theory’s prediction is falsified the theory itself is to be treated as false. Pseudo-sciences, among which Popper includes Marxism and Freudianism, are insulated from criticism, able to explain and incorporate any fact. They do not make any firm predictions, but are capable of explaining, or explaining away, anything that comes up.

This is a second way in which science might be seen as a formal activity. According to Popper, scientific theories are imaginative creations, and there is no method for creating them. They are free-floating, their meaning not tied to observations as for the positivists. However, there is a strict method for evaluating them. Any theory that fails to make risky predictions is ruled unscientific, and any theory that makes failed predictions is ruled false. A theory that makes good predictions is provisionally accepted - until new evidence comes along. Popper’s scientist is first and foremost skeptical, unwilling to accept anything as proven, and willing to throw away anything that runs afoul of the evidence. On this view, progress is probably best seen as the successive refinement and enlargement of theories to cover increasing data. While science may or may not reach the truth, the process of conjectures and refutations allows it to encompass increasing numbers of facts.

Like the central idea of positivism, falsificationism faces some immediate problems. Scientific theories are generally fairly abstract, and few make hard predictions without adopting a whole host of extra assumptions (e.g. Putnam 1981); so on Popper’s view most scientific theories would be unscientific. Also, when theories are used to make incorrect predictions, scientists often - and quite reasonably - look for reasons to explain away the observations or predictions, rather than rejecting the theories. Nonetheless, there is something attractive about the idea that (potential) falsification is the key to solid scientific standing, and so falsificationism, like logical positivism, still has adherents today.

For both positivism and falsificationism, the features of science that make it scientific are formal relations between theories and data, whether through the rational construction of theoretical edifices on top of empirical data or the rational dismissal of theories on the basis of empirical data. There are analogous views about mathematics; indeed, formalist pictures of science probably depend on stereotypes of mathematics as a logical or mathematical activity.

Box 1.2 The Duhem–Quine thesis

The Duhem-Quine thesis is the claim that a theory can never be conclusively tested in isolation: what is tested is an entire framework or a web of beliefs. This means that in principle any scientific theory can be held in the face of apparently contrary evidence. Though neither of them put the claim quite this baldly, Pierre Duhem and W.V.O. Quine, writing in the beginning and middle of the twentieth century respectively, showed us why.

How should one react if some of a theory’s predictions are found to be wrong? The answer looks straightforward: the theory has been falsified, and should be abandoned. But that answer is too easy, because theories never make predictions in a vacuum. Instead, they are used, along with many other resources, to make predictions. When a prediction is wrong, the culprit might be the theory. However, it might also be the data that set the stage for the prediction, or additional hypotheses that were brought into play, or measuring equipment used to verify the prediction. The culprit might even lie entirely outside this constellation of resources: some unknown object or process that interferes with observations or affects the prediction.

To put the matter in Quine’s terms, theories are parts of webs of belief. When a prediction is wrong, one of the beliefs no longer fits neatly into the web. To smooth things out - to maintain a consistent structure - one can adjust any number of the web’s parts. With a radical enough redesign of the web, any part of it can be maintained, and any part jettisoned. One can even abandon rules of logic if one needs to!

When Newton’s predictions of the path of the moon failed to match the data he had, he did not abandon his theory of gravity, his laws of motion, or any of the calculating devices he had employed. Instead, he assumed that there was something wrong with the observations, and he fudged his data. While fudging might seem unacceptable, we can appreciate his impulse: in his view, the theory, the laws, and the mathematics were all stronger than the data! Later physicists agreed. The problem lay in the optical assumptions originally used in interpreting the data, and when those were changed Newton’s theory made excellent predictions.

Does the Duhem-Quine thesis give us a problem of induction? It shows that multiple resources are used (not all explicitly) to make a prediction, and that it is impossible to isolate for blame only one of those resources when the prediction appears wrong. We might, then, see the Duhem-Quine thesis as posing a problem of deduction, not induction, because it shows that when dealing with the real world, many things can confound neat logical deductions.

But there are other features of the popular snapshot of science. These formal relations between theories and data can be difficult to reconcile with an even more fundamental intuition about science: Whatever else it does, science progresses toward truth, and accumulates truths as it goes. We can call this intuition realism, the name that philosophers have given to the claim that many or most scientific theories are approximately true.

First, progress. One cannot but be struck by the increases in precision of scientific predictions, the increases in scope of scientific knowledge, and the increases in technical ability that stem from scientific progress. Even in a field as established as astronomy, calculations of the dates and times of astronomical events continue to become more precise. Sometimes this precision stems from better data, sometimes from better understandings of the causes of those events, and sometimes from connecting different pieces of knowledge. And occasionally, the increased precision allows for new technical ability or theoretical advances.

Second, truths. According to realist intuitions, there is no way to understand the increase in predictive power of science, and the technical ability that flows from that predictive power, except in terms of an increase of truth. That is, science can do more when its theories are better approximations of the truth, and when it has more approximately true theories. For the realist, science does not merely construct convenient theoretical descriptions of data, or merely discard falsified theories: When it constructs theories or other claims, those generally and eventually approach the truth. When it discards falsified theories, it does so in favor of theories that better approach the truth.

Real progress, though, has to be built on more or less systematic methods. Otherwise, there would only be occasional gains, stemming from chance or genius. If science accumulates truths, it does so on a rational basis, not through luck. Thus, realists are generally committed to something like formal relations between data and theories.

Turning from philosophy of science, and from issues of data, evidence, and truth, we see a social aspect to the standard picture of science. Scientists are distinguished by their even-handed attitude toward theories, data, and each other. Robert Merton’s functionalist view, discussed in Chapter 3, dominated discussions of the sociology of science through the 1960s. Merton argued that science served a social function, providing certified knowledge. That function structures norms of scientific behavior, those norms that tend to promote the accumulation of certified knowledge. For Merton, science is a well-regulated activity, steadily adding to the store of knowledge.

Box 1.3 Underdetermination

Scientists choose the best account of data from among competing hypotheses. This choice can never be logically conclusive, because for every explanation there are in principle an indefinitely large number of others that are exactly empirically equivalent. Theories are underdetermined by the empirical evidence. This is easy to see through an analogy.

Imagine that our data is the collection of points in the graph on the left (Figure 1.1). The hypothesis that we create to “explain” this data is some line of best fit. But what line of best fit? The graph on the right shows two competing lines that both fit the data perfectly.

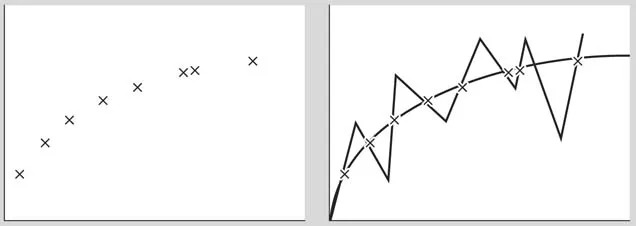
Clearly there are infinitely many more lines of perfect fit. We can do further testing and eliminate some, but there will always be infinitely many more. We can apply criteria like simplicity and elegance to eliminate some of them, but such criteria take us straight back to the first problem of induction: how do we know that nature is simple and elegant, and why should we assume that our ideas of simplicity and elegance are the same as nature’s?

When scientists choose the best theory, then, they choose the best theory from among those that have been seriously considered. There is little reason to believe that the best theory so far considered, out of the infinite numbers of empirically adequate explanations, will be the true one. In fact, if there are an infinite number of potential explanations, we could reasonably assign to each one a probability of zero.

The status of underdetermination has been hotly debated in philosophy of science. Because of the underdetermination argument, some philosophers (positivists and their intellectual descendants) argue that scientific theories should be thought of as instruments for explaining and predicting, not as true or realistic representations (e.g. van Fraassen 1980). Realist philosophers, however, argue that there is no way of understanding the successes of science without accepting that in at least some circumstances evaluation of the evidence leads to approximately true theories (e.g. Boyd 1984; see Box 6.2).

On Merton’s view, there is nothing particularly “scientific” about the people who do science. Rather, science’s social structure rewards behavior that, in general, promotes the growth of knowledge; in principle it also penalizes behavior that retards the growth of knowledge. A number of other thinkers hold that position, such as Popper (1963) and Michael Polanyi (1962), who both support an individualist, republican ideal of science, for its ability to progress.

Common to all of these views is the idea that standards or norms are the source of science’s success and authority. For positivists, the key is that theories can be no more or less than the logical representation of data. For falsificationists, scientists are held to a standard on which they have to discard theories in the face of opposing data. For realists, good methods form the basis of scientific progress. For functionalists, the norms are the rules governing scientific behavior and attitudes. All of these standards or norms are attempts to define what it is to be scientific. They provide ideals that actual scientific episodes can live up to or not, standards to judge between good and bad science. Therefore, the view of science we have seen so far is not merely an abstraction from science, but is importantly a view of ideal science.

A View of Technology

Where is technology in all of this? Technology has tended to occupy a secondary role, for a simple reason: it is often thought, in both popular and academic accounts, that technology is the relatively straightforward application of science. We can imagine a linear model of innovation, from basic science through applied science to development and production. Technologists identify needs, problems, or opportunities, and creatively combine pieces of knowledge to address them. Technology combines the scientific method with a practically minded creativity.

As such, the interesting questions about technology are about its effects: Does technology determine social relations? Is technology humanizing or dehumanizing? Does technology promote or inhibit freedom? Do science’s current applications in technologies serve broad public goals? These are important questions, but as they take technology as a finished product they are normally divorced from studies of the creation of particular technologies.

If technology is applied science then it is limited by the limits of scientific knowledge. On the common view, then, science plays a central role in determining the shape of technology. There is another form of determinism that often arises in discussions of technology, though one that has been more recognized as controversial. A number of writers have argued that the state of technology is the most important cause of social structures, because technology enables most human action. People act in the context of available technology, and therefore people’s relations among themselves can only be understood in the context of technology. While this sort of claim is often challenged - by people who insist on the priority of the social world over the material one - it has helped to focus debate almost exclusively on the effects of technology.

Lewis Mumford (1934, 1967) established an influential line of thinking about technology. According to Mumford, technology comes in two varieties. Polytechnics are “life-oriented,” integrated with broad human needs and potentials. Polytechnics produce small-scale and versatile tools, useful for pursuing many human goals. Monotechnics produce “mega machines” that can increase power dramatically, but by regimenting and dehumanizing. A modern factory can produce extraordinary material goods, but only if workers are disciplined to participate in the working of the machine. This distinction continues to be a valuable resource for analysts and critics of technology (see, e.g., Franklin 1990, Winner 1986).

In his widely read essay “The Question Concerning Technology” (1977 [1954]), Martin Heidegger develops a similar position. For Heidegger, distinctively modern technology is the application of science in the service of power; this is an objectifying process. In contrast to the craft tradition that produced individualized things, modern technology creates resources, objects made to be used. From the point of view of modern technology, the world consists of resources to be turned into new resources. A technological worldview thus produces a thorough disenchantment of the world.

Through all of this thinking, technology is viewed as simply applied science. For both Mumford and Heidegger modern technology is shaped by its scientific rationality. Even the pragmatist philosopher John Dewey (e.g. 1929), who argues that all rational thought is instrumental, sees science as theoretical technology (using the word in a highly abstract sense)...