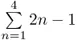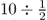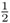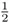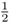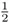The Problem with Math Is English

A Language-Focused Approach to Helping All Students Develop a Deeper Understanding of Mathematics

Concepcion Molina

• Publisher: Jossey-Bass
• Year: 2012
• ISBN:
  9781118237021
• Edition: 1
• Topic: Education
• Subtopic: Teaching Mathematics

Teaching K-12 math becomes an easier task when everyone understands the language, symbolism, and representation of math concepts

Published in partnership with SEDL, The Problem with Math Is English illustrates how students often understand fundamental mathematical concepts at a superficial level. Written to inspire?aha? moments, this book enables teachers to help students identify and comprehend the nuances and true meaning of math concepts by exploring them through the lenses of language and symbolism, delving into such essential topics as multiplication, division, fractions, place value, proportional reasoning, graphs, slope, order of operations, and the distributive property.

• Offers a new way to approach teaching math content in a way that will improve how all students, and especially English language learners, understand math
  
• Emphasizes major attributes of conceptual understanding in mathematics, including simple yet deep definitions of key terms, connections among key topics, and insightful interpretation

This important new book fills a gap in math education by illustrating how a deeper knowledge of math concepts can be developed in all students through a focus on language and symbolism.

Chapter One

The Problem with Math Is English (and a Few Other Things)

Many people do not consider English as playing a significant role in math, except in word problems. My hope in the forthcoming pages is to change that perspective. A well-known proverb says that to truly understand another's perspective, you must walk a mile in that person's shoes. Not everyone has experienced the struggle of learning both academic content and a new language at the same time. True, this double burden makes learning mathematics much more of a challenge. However, the phrase “the problem with math is English” applies to all students, not just those whose native language is not English. Language struggles are embedded in mathematics, which in many ways is its own language. These problems often occur at the critical juncture of math instruction and content. Two major issues in mathematics education that result from this merger are often overlooked: (1) the language and symbolism of mathematics, which in turn greatly influence (2) the mathematics itself—the content that we teach—and by association, how we communicate that content. The following scenarios introduce some key concepts related to these issues, which this book will explore in-depth.

Why Language and Symbolism?

Imagine you are a middle school student taking the state's required progress exam in mathematics. As you begin the test, you feel confident about your answers to the first few items. But then you read Item 5: “Find the arglif of a nopkam if the betdosyn is 12.” Try as you will, the problem has you stumped. You finally give up, make a guess, and move on to the next problem. Unfortunately, you come across 14 other test items that confuse you in similar ways. Once again, the best you can do is guess at the answers. Later, you find out you did not pass the exam primarily because of those 15 items.

When most people see or hear the term mathematics, the initial thoughts that come to mind are numbers, computation, rules, and procedures. But the root cause of the student's inability to solve Item 5 is not because of a lack of knowledge of computation, rules, or procedures. If the strange terms arglif, nopkam, and betdosyn meant “area,” “circle,” and “diameter,” respectively, Item 5 would become the following: “Find the area of a circle if the diameter is 12.” However, if a student does not know the meanings of area, circle, and diameter, the terms might as well be arglif, nopkam, and betdosyn because they still hold no meaning.

This scenario is a rudimentary example of the key role that language plays in the understanding of mathematics. The student's difficulty is not in reading English, but in understanding the language of mathematics, and it makes no difference whether the student is fluent in English or not. A language problem still exists. Although perhaps not obvious, language is as critical in mathematics as in any other discipline. Moreover, the role of language in mathematics entails far more than vocabulary or definitions, encompassing a broad landscape of language-based issues, which are explored in this book.

Beyond Words: The Symbolism of Mathematics

---

Box 1.1

Solve the two tasks below:

a. n = 1 + 3 + 5 + 7

b.

---

For many people, the first problem in Box 1.1 is child's play, whereas the second poses a serious challenge. The interesting paradox about these two problems is that although the second seems far more difficult, they are, in fact, the same problem. They are just presented differently. The first problem seems simple because most people can easily interpret what the numerals and symbols are telling them to do. The second problem, however, will literally be Greek to many people because they have no idea what those symbols mean. The problem becomes much simpler once the symbols are explained. The symbol ∑ is a summation symbol. The n =1 in the subscript means that 1 is the first value of n in the expression 2n – 1, and the superscript 4 indicates the last value to be used in that expression. Thus, the task is to determine the value of 2n – 1 when n is 1, 2, 3, and 4, and then to find the sum of those values. These steps result in the expression 1 + 3 + 5 + 7. Simple!

These two problems illustrate the key role of symbolism and visual representation in mathematics. The interpretation and subsequent understanding of mathematics concepts are heavily dependent not only on language but also on the symbols that are an inherent component of the discipline. These two problems also illustrate a scenario seen in far too many classrooms when concepts or ideas in mathematics that are actually quite simple are presented in a way that is far more complex, much to the detriment of student learning. In other words, there are too many instances in mathematics instruction where a simple concept or idea is somehow prodded and molded, either by the math education system or teachers, and unveiled to students as something that appears to be far more complicated than it really is.

The Language of Mathematics Instruction

---

Box 1.2

You have been teaching the challenging concept and skill of division by a proper fraction. You write the problem

on the board. You then state, “Class, how many times does

go into 10?”

---

Refer to the question asked in Box 1.2. If teachers tend to teach the same way they were taught, it follows they will tend to teach using the same language. Over the years, numerous elementary and middle school teachers have presented the expression 10 ÷

as the question, “How many times does

go into 10?” As students themselves, these teachers accepted this interpretation of the symbols and moved on regardless of how much sense the interpretation made—or did not make—to them. Once they became teachers, they used the same language, thus passing on the torch to their students. Quite honestly, what can a student create to model a context where

goes into 10? The question as posed really makes no sense. The language of instruction in mathematics often makes the conceptual meaning almost impossible to grasp, but students survive by blindly following procedures that enable them to get the correct answers that result in good grades. As educators, however, we must reflect and ask ourselves what level of mathematics are students actually learning, and is that depth of knowledge acceptable?

What We are Teaching

---

Box 1.3

Next week's unit of instruction will focus on the multiplication of mixed numbers. You need to ensure that students have the prerequisite skills and knowledge to learn this new topic. What are these prerequisite skills and knowledge? Make a list.

---

Your generated list from Box 1.3 would likely include many prerequisite skills or concepts that focus on how to multiply mixed numbers. Think of your experiences as a math student and, if applicable, as a math teacher. Much of the instruction and learning in math classrooms is focused on how-tos. In the United States, we value good old American know-how. To learn mathematics at a deep conceptual level, however, know-how is not enough. Just as important, if not more so, is good old American know-what and know-why. In other words, students need to understand what a basic concept is and why that concept works as it does. In the scenario in Box 1.3, students need first to understand what multiplication is conceptually, then use that knowledge to understand why the process works as it does. Knowing only how to multiply, at best, results in basic memorization of rules and procedures.

Not surprisingly, many adults in the United States perceive mathematics simply as a conglomeration of facts, rules, computations, and procedures. After all, that is the type of mathematics they were taught. The K–12 math education system often focuses on arithmetic and efficiency (or algorithms), but mathematics is far more than that. If teachers only know, and subsequently teach, arithmetic and algorithms rather than a conceptual understanding of mathematics, then that limited knowledge will be the baton passed on to future generations.

What Is Missing: The Need for Definitions

An interesting paradox in mathematics is that one can know how to do something without understanding what the concept or process truly is. For example, students can know how to multiply without understanding what multiplication is conceptually. I successfully navigated numerous math courses knowing how to use π in formulas while having no clue as to what π meant as a concept. Quite literally, the what is missing from math instruction. Since a definition tells us what something is, it makes sense to emphasize definitions as a core element of instruction.

---

Box 1.4

Answer the following:

a. Define equation (noun).

b. Define graph (noun).

---

Defining key mathematical terms helps students build their understanding of important concepts. Students should be able to provide precise yet simple definitions of basic terms, such as those in Box 1.4. For teachers, these types of definitions paint a clear picture of students' depth of understanding. Incorrect student responses can reveal misunderstandings and gaps in knowledge. In addition, patterns that emerge from students' definitions of basic concepts can provide clues about the effectiveness of instruction, the curriculum, and even the larger mathematics education system.

Patterns of Misunderstanding

As a young high school math teacher, I often made assumptions regarding students' content knowledge, especially their mastery of fundamental concepts in earlier grades. I adopted the strategy of having students define basic math concepts not only to build understanding but also to expose the areas where students' knowledge was weak. The approach revealed some interesting patterns over the years. For example, high school students in higher-level math classes most commonly define an equation, one of the most basic concepts in mathematics, as “when you solve for x.” This definition is a clear misconception of what an equation is, but the root cause was not so evident. After much reflection and analysis, I realized the origin lay in the state's mathematics content standards. In the state standards in effect at that time, the term equation did not appear until the sixth grade. Moreover, the context for this first appearance focused on learning to solve simple linear equations. This initial focus had likely contributed to students' misconception of an equation being “when you solve for x.”

The concept of an equation is usually defined as a mathematical sentence that states that one quantity is the same as another quantity. In other words, the quantity expressed on the left side of the equal sign is the same as the quantity expressed ...