Analogical Reasoning in Children

Usha Goswami

• Publisher: Psychology Press
• Year: 2013
• ISBN:
  9781317775393
• Edition: 1
• Topic: Psychology
• Subtopic: History & Theory in Psychology
• Index: Psychology

Analogical reasoning is a fundamental cognitive skill, involved in classification, learning, problem-solving and creative thinking, and should be a basic building block of cognitive development. However, for a long time researchers have believed that children are incapable of reasoning by analogy. This book argues that this is far from the case, and that analogical reasoning may be available very early in development. Recent research has shown that even 3-year-olds can solve analogies, and that infants can reason about relational similarity, which is the hallmark of analogy.
The book traces the roots of the popular misconceptions about children's analogical abilities and argues that when children fail to use analogies, it is because they do not understand the relations underlying the analogy rather than because they are incapable of analogical reasoning. The author argues that young children spontaneously use analogies in learning, and that their analogies can sometimes lead them into misconceptions. In the "real worlds" of their classrooms, children use analogies when learning basic skills like reading, and even babies seem to use analogies to learn about the world around them.

Chapter One
Reasoning by Analogy

Reasoning by analogy is a central component of human cognition. It is involved in classification and in learning, it provides a tool for thought and explanation, and it is important for scientific discovery and creative thinking. Its fundamental role in reasoning has been widely recognised in cognitive psychology, where it has been the focus of recent research in areas as diverse as learning by example, the nature of conceptual structure, creative problem solving, and artificial intelligence (e.g. see Vosniadou & Ortony, 1989). The importance of analogical reasoning has also been widely documented in the history of science.

Many classic scientific discoveries were made by analogy. A famous example is that of Archimedes (3rd century B.C.), who had been asked to determine whether base metal had been substituted for gold in an intricately designed crown ordered by his king. Although the weight per volume of pure gold was known, the crown was so ornate that its volume was impossible to measure. Archimedes was unable to see a solution to this problem until he went home and stepped into the bath. He then saw an analogy between the volume of water displaced by his body as he got into his bath, and the volume of water that would be displaced by the crown. The problem was solved. By immersing the crown in water, he could work out whether it was made of pure gold.

Another famous example of analogy in science is Kepler's analogy between religion and the relationship between the motion of the planets and their distance from the sun. He wrote: "My ceaseless search concerned primarily three problems, namely the number, size and motion of the planets... by that beautiful analogy between the stationary objects, namely the sun, the fixed stars, and the space between them, with God the Father, the Son, and the Holy Ghost." The analogy mapped out as follows: "The sun in the middle of the moving stars, himself at rest and yet the source of motion, carries the image of God the Father and Creator. He distributes his motive force through a medium which contains moving bodies, even as the Father creates through the Holy Ghost" (cited in Gordon, 1979). This analogy eventually led Keppler to an operational theory of celestial mechanics that resulted in the notion of gravity.

Kepler's discovery also illustrates an important point about the role of analogy in the history of science, a point which applies equally to Aristotle. Most analogical breakthroughs were not miraculous in the sense that their discoverers took a step into the complete unknown. Instead, much of the conceptual preparation for the discoveries had already taken place, and it was probably only a matter of time before somebody made the analogical connection. Nevertheless, the discoverers did make a genuine contribution to the development of knowledge, as their analogies provided a genuinely new way of thinking about previously known phenomena. This point was put succinctly in 1909 by the French mathematician Poincaré, who noted the creative role played by analogies in theory development in mathematics: "the mathematical facts worthy of being studied are those which, by their analogy with other facts, are capable of leading us to the knowledge of a mathematical law just as experiential facts lead us to the knowledge of a physical law. They are those which reveal to us unsuspected kinship between other facts, long known, but wrongly believed to be strangers to one another" (cited in Gordon, 1979). The role of conceptual knowledge (the facts) in successful analogising will be one of the themes of this book.

Analogies are often used to teach science as well. A familiar example is using hydrostatics as an analogy for electricity, with the behaviour of flowing water providing an analogue for the activity of the electricity. The wire or conductor of the electricity is likened to a pipe through which the water flows, the battery is similar to a pool or reservoir, electrical voltage is analogous to water pressure, and a resistor is like a restriction in the water pipe. The fact that the presence of a resistor will decrease electrical current in a wire can then by understood by analogy to a restriction in a water pipe which will decrease the water flow in that pipe. Similarly, the fact that an increase in voltage occurs when two batteries are connected in series is explained by analogy to the increase in water pressure that would result from connecting two reservoirs of water that differed in height. However, prior conceptual knowledge will play a role here, too. Useful pedagogical analogies depend on a certain degree of knowledge on the part of the student: the relevant relationships within the conceptual system on which the analogy is based must already be understood. A student who did not understand hydrostatics would not learn anything about electricity from the preceding analogy.

Analogies can facilitate problem-solving as well as learning and discovery, as many experiments have shown. For example, Gick and Holyoak (1980, 1983) designed a paradigm based on Duncker's X-ray problem to investigate the benefits conferred by analogy. In Duncker's problem, surgeons need to destroy an internal tumour with X-rays without simultaneously destroying the surrounding healthy tissue. It is impossible to use invasive surgery, as the patient will die. The solution is to use a number of weak X-rays that individually will not harm body tissue, and to achieve the appropriate strength by converging the rays onto the tumour. Only 5% of Duncker's students thought of this "convergence solution" spontaneously.

Gick and Holyoak's idea was to tell their subjects about an appropriate analogy prior to presenting them with Duncker's problem. The analogy concerned a famous general who had successfully captured a fortress surrounded by mined approach roads. Although the general needed the strength of his entire army to capture the fortress, the weight of all his men was bound to trigger the mines. The general solved this problem by dividing his army into smaller units that were too light to set off the mines, and then sending each unit down a separate road, so that they converged onto the fortress in a united attack. Students who learned about this analogy were more likely to think of the "convergence solution" to Duncker's problem. So the right analogy can significantly improve problem-solving performance.

Analogies are thus important in learning, problem solving and discovery. Surprisingly, however, developmental psychology has been less ready to assign a central role to analogical reasoning. In fact, children's use of analogy was not widely studied until fairly recently. The reasons for this neglect were partly historical. According to Piagetian theory, the ability to reason by analogy was a late-developing skill, emerging at around 11-12 years of age during the "formal-operational" period of reasoning. Younger children were thought to be incapable of reasoning by analogy, and consequently few people investigated their analogical reasoning skills.

The traditional view of analogical development was supported by research in psychometrics. Psychometric research had shown that many children, even at 11-12 years of age, were unable to complete simple analogies like pig:boar::dog:? (wolf). When given these analogies, younger children typically produced non-analogical associative responses, like pig:boar::dog:cat (e.g. Achenbach, 1971). Psychometricians used these "item" or "classical" analogies as a measure of I.Q., regarding them as a test of the development of reasoning skills. Let us begin by examining the kind of reasoning that these tests of analogy require in more detail.

Classical Analogies

The term "classical analogy" is derived from Aristotle. He defined analogy as "an equality of proportions ... involving at least 4 terms ... when the second is related to the first as the fourth is to the third" (Aristotle, Metaphysics). Aristotle's definition of analogy concentrates on the need to equate the relations between the pairs of terms in the analogy, which are usually represented by the format A:B::C:D (e.g. wide:narrow::high:low). The relation between the C and the D terms should be equivalent to that linking the A and the B terms.

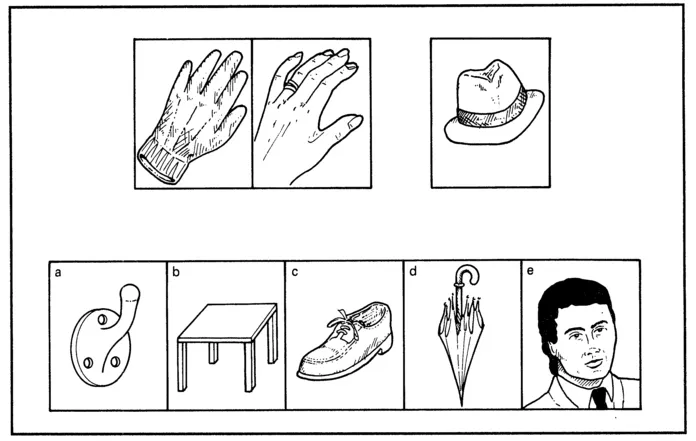
This "relational similarity" requirement is made very clear in most standardised tests of analogical reasoning, as the instructions from one such test demonstrate: "In each of the sequences below, Figure A is to Figure B as Figure C is to ONE of the Figures D. Choose the Figure in D that bears the same relation to Figure C as Figure B does to Figure A" (NFER Picture Test A, Stuart, 1977). An analogy item from this test is shown in Fig. 1.1. Younger children typically do more poorly than older children on these tests.

Aristotle's criterion of an equality of relations is generally accepted to be the "hallmark" of analogical reasoning. According to the traditional view, younger children are unable to reason by analogy because they are incapable of using this hallmark. They do not understand relational similarity. The tendency of younger children to solve analogies by producing associative responses provides apparent support for this view.

For example, Gallagher and Wright (1977) asked a group of 10-year-olds to complete verbal multiple-choice classical analogies like food:body::rain: (water, storm, coat, ground). Most children selected the incorrect response water, explaining their choice with justifications such as "Water falls from the sky". These justifications ignored relational similarity. Piaget and his colleagues gave 5- to 6-year-olds a classical analogy task based on pictures, and found a similar failure to equate relations. For example, Bol. (aged 6 years, 6 months) was given some pictures that included the analogy nurse:syringe::barber:scissors. He selected the pictures of the nurse and of the syringe, then took the picture of the barber and paused, non-plussed: "I'm looking for a washbasin" (Piaget, Montangero & Billeter, 1977).

FIG. 1.1. A typical picture analogy from the NFER Picture Test A (reproduced with permission from Stuart, 1977.).

Problem Analogies

A different approach to studying analogical reasoning in children is to give them problems to solve by analogy. Research using this approach initially seemed to support the idea that younger children could not use relational correspondences. In the "problem analogy" paradigm, the relational similarity that children have to reason about is between two problems and their solutions. The children are told about one problem, usually called the base problem, and are then given a similar problem to solve, usually called the target problem. The assumption is that children who can recognise and use relational similarity should solve the target problem by using an analogous solution to that in the base.

In one such experiment, young children (5-6 years) learned about a base problem in which a magic genie rolled his carpet into a tube to provide a passage for some precious jewels. This was meant to provide an analogy to the target problem, which involved transporting some small rubber balls from one location to another. The children were expected to work out that a possible solution to this problem was to roll up a sheet of paper that had been provided by the experimenters, and make a passage for the balls. The relational similarity was meant to be "rolling up a flat and flexible object" (Holyoak, Junn & Billman, 1984). However, the majority of children failed to see the intended relational correspondence between the carpet and the paper, and totally ignored the sheet of paper when devising their solutions. The relational similarity between the base problem and the target problem was evident to the experimenters, but it was not so evident to their subjects.

“Higher-order” vs “Lower-order” Relations

Although the classical and the problem analogy paradigms have been used in quite separate research literatures, they seem to be testing the same basic reasoning skills. Both are trying to measure children's ability to recognise and to use similarities between relations. The ability to reason about relational similarity would not appear to be particularly sophisticated. However, the claim that this ability was not present until adolescence went unchallenged for many years. To discover why this was the case, we must consider the distinction that was traditionally made between the kinds of relations involved in an analogy.

There was a pervasive belief that two levels of reasoning were involved in analogy, and that these corresponded to the apprehension of two different kinds of relations. In classical analogies, the two kinds of relation were (1) lower-order or first-order relations, and (2) higher-order or second-order relations (e.g. Lunzer, 1965; Inhelder & Piaget, 1958). The distinction between these two kinds of relation was believed to have psychological reality.

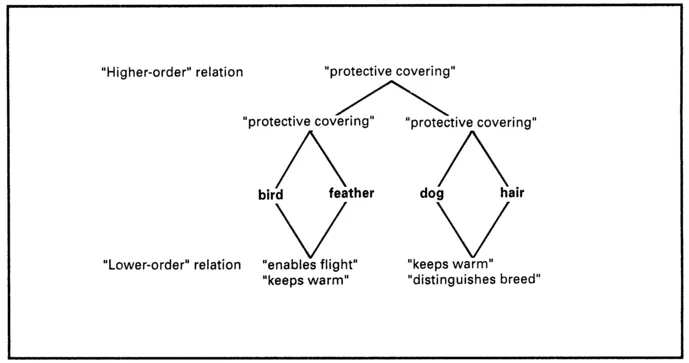
Lower-order relations are traditionally denned as the relations between the A and the B terms and between the C and the D terms in an analogy. For example, in the analogy bird:feathers::dog:hair, the "lower-order" relations relate the different elements in each pair of terms, such as birds and feathers. One possible "lower-order" relation would be "enables flight", as the aerodynamic properties of feathers help birds to fly. Another possible "lower-order" relation would be "keeps warm", as feathers help to protect birds from the cold.

These "lower-order" relations are thought to be an ontologically simpler kind of relation than "higher-order" relations. "Higher-order" relations link the "lower-order" relations, so a "higher-order" relation is a relationship between the pairs of elements in the analogy. The "higher-order" relation in the analogy bird:feathers::dog:hair would be something like "protective covering". "Higher-order" relations are believed to require a more complex kind of reasoning than "lower-order" relations, as they are "second-order" relations. The two kinds of relation are shown in Fig. 1.2.

FIG. 1.2. The traditional view of the two sets of relations in an analogy.

A similar distinction between two levels of reasoning is found in problem analogies. The distinction here is usually between reasoning about the relations in a given problem, and reasoning about the objects in which those relations are embedded. Younger children and novice reasoners have been thought to focus on the objects at the expense of the relations between them (Gentner, 1983, 1989). For example, in the genie analogy mentioned earlier, younger children might focus on the genie and his carpet rather than on the "rolling" solution. This would lead them to look for similar objects in the rubber balls problem, and so they would ignore similar relations.

Older children and more expert reasoners are thought to focus on relational commonalities when trying to solve analogies, enabling them to extract "higher-order" structure. They go beyond the "mere appearance" of the objects in the base and the target problems, and reason about the relations between them. In the genie analogy, expert reasoners would focus on the "rolling a flexible material" relation, ignoring the superficial dissimilarity between the sheet of paper and the carpet. In richer problem analogies with many relations, expert reasoners would focus on "higher-order relations with inferential import" rather than on isolated relations (Gentner, 1983). For example, in Rutherford's analogy between a hydrogen atom and the solar system (both are orbiting systems), expert reasoners would focus on the cause-effect relations that govern orbiting rather than on isolated relations such as the sun being hotter than the planets.

Structural Theories of Analogical Reasoning

The idea that there was a clear distinction between "lower-order" and "higher-order" levels of reasoning has traditionally provided a neat explanation of younger children's apparent failure to solve analogies. Younger children were simply said to be incapable of reasoning about "higher-order" relations. They were restricted to reasoning at the "lower-order" relational level, where they reasoned in a successive way about the relations between the pairs of terms in an analogy. To younger children, it was quite consistent to solve an analogy by thinking of one relation to link the A:B pair, and quite another relation to link the C:D pair. The development of the ability to reason about similarities between these relations reflecte...