Hands-On Geometry

Constructions With a Straightedge and Compass (Grades 4-6)

Christopher M. Freeman

• Publisher: Routledge
• Year: 2021
• ISBN:
  9781000493306
• Edition: 1
• Topic: Education
• Subtopic: Education General

Put compasses into your students' hands and behold the results! Hands-On Geometry teaches students to draw accurate constructions of equilateral triangles, squares, and regular hexagons, octagons, and dodecagons; to construct kites and use their diagonals to construct altitudes, angle bisectors, perpendicular bisectors, and the inscribed and circumscribed circles of any triangle; to construct perpendicular lines and rectangles, parallel lines, and parallelograms; and to construct a regular pentagon and a golden rectangle.Students will enjoy fulfilling high standards of precision with these hands-on activities. Hands-On Geometry provides the background students need to become exceptionally well prepared for a formal geometry class. The book provides an easy way to differentiate instruction: Because the lessons are self-explanatory, students can proceed at their own pace, and the finished constructions can be assessed at a glance.Grades 4-6

Chapter 1:
Lines and Arcs

DOI: 10.4324/9781003235477-1

Name____________________________________ Date__________________

Introduction: The Straightedge and Compass Tools

For more than 2,000 years, mathematicians have used two basic tools to construct geometric figures: a compass to draw circles, and a straightedge to draw lines. With these simple tools, you will learn to construct triangles, hexagons, squares, kites, perpendicular lines, parallel lines, and lots of other figures.

A compass has a sharp point at one end to hold it steady at the center of the circle, and it has a pencil point at the other end to draw the circle. The distance between the sharp point and the pencil point is called the radius. You will use a compass to draw circles and arcs. To draw a straight line, you will pull a pencil tip along a straightedge. A straightedge is different from a ruler, because a straightedge has no marks on it. If you use a ruler, you should ignore the inch or centimeter markings. To measure length, you will use the radius of the compass.

Name_______________________________________ Date._______________________

Lesson 1.1
Construct a Circle by Center and Point

A point is a location. We often represent a point with a dot (.), but any dot is really too big because the point is at the center of the dot. We name points with capital letters, like points C and P below.

One way to construct a circle starts with one point that will be its center and another point that will be on the circle. Follow the directions below to construct the circle with center C and passing through P. Your construction will look like the picture to the right.

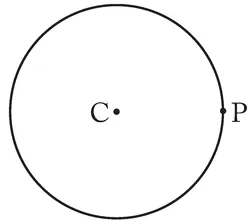
1. Put the sharp point of the compass onto C and hold it there.
2. Adjust the compass radius so that the pencil point rests gently on the point P.
3. Hold the compass at its top, not by the pencil
4. Lean the compass slightly in the direction you want to draw
5. Start drawing the circle through P; if the curve doesn't go exactly through the center of point P, adjust the radius and start again.
6. Lightly draw the circle with your compass.

Name________________________________________ Date_____________________________

Lesson 1.2
Construct a Line and an Equilateral Triangle

A basic postulate of geometry is that two points determine a line. In practice, drawing this line is not as trivial as it may sound. If you work carefully, your construction will look like the picture below. Follow the directions below to construct a line.

1. Place your straightedge just under the two points P and Q below. Hold it steady.
2. As you pull your pencil along the straightedge, make sure that the pencil tip goes through the center of each point. If not, change the angle of your pencil, or adjust your straightedge. Be precise! Make sure your pencil is sharp.
3. Draw an arrowhead at each end of your line.

The arrowheads indicate that lines go on forever in both directions. We name a line using any two points on it with a line symbol above them, such as

.The piece of a line between two endpoints (like P and Q above) is called a line segment, or segment for short. We name a segment using its two endpoints with a bar on top, such as

Segments don't go on forever, they end at their endpoints.

Now you will construct an equilateral triangle, in which all three sides are segments of equal length. Your construction will look like the picture to the right.

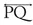
1. Use your straightedge to construct the line segment
   
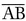
2. Construct a circle with center A and passing through B,
3. Construct another circle with center B and passing through A.
4. Locate a point where the two circles intersect and label it C. (You don't need to draw a dot because the location where two circles cross is a point.)
5. Use your straightedge to construct segments
   
   and
   
   . You now have equilateral △ ABC!

Name_______________________________________ Date___________________________

Lesson 1.3
Draw an Arc and Copy a Segment

Just as a segment is a piece of a line, an arc is a piece of a circle.

Which point, A, B, or C, is the center of the arc shown below? ______________

To check your answer, put the sharp point of your compass on A, adjust your radius, and try to draw the arc. Then put the sharp point on B and try to draw the arc. Then repeat using point C. (Was your answer correct?)

To copy a segment means to make another segment with the same length. Don't use a ruler to measure length—use the radius of your compass! When you follow the directions below, you will construct a copy of segment

, called

. Your construction will look like this picture:

Use segment

and line m, below.

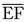
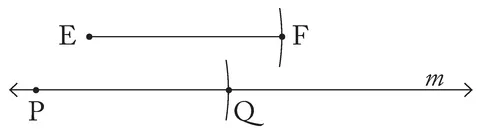
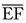
1. Anywhere on the line m, mark a tiny dot and label it P.
2. Put the sharp point of your compass on E, and adjust the radius so you can draw a short arc through F.
3. Don't change the radius, but move the sharp point to P and draw a short ...