Introduction to Vision Science

Richard A. Clement

• Publisher: Routledge
• Year: 2016
• ISBN:
  9781317244165
• Edition: 1
• Topic: Psychology
• Subtopic: History & Theory in Psychology
• Index: Psychology

Different animals have different visual systems and so presumably have different ways of seeing. How does the way in which we see depend on the optical, neural and motor components of our visual systems? Originally published in 1993, the mathematical tools needed to answer this question are introduced in this book. Elementary linear algebra is used to describe the transformations of the stimulus that occur in the formation of the optical, neural and motor images in the human visual system. The distinctive feature of the approach is that transformations are specified with enough rigour for readers to be able to set up their own models and generate predictions from them.

Underlying the approach of this book is the goal of providing a self-contained source for the derivation of the basic equations of vision science. An introductory section on vector and matrix algebra covers the mathematical techniques which are applied to both sensory and motor aspects of the visual system, and the intervening steps in the mathematical arguments are given in full, in order to make the derivation of the equations easier to follow.

A subsidiary goal of this book is to demonstrate the utility of current desktop computer packages which make the application of mathematics very easy. All the numerical results were produced using only a spreadsheet or mathematics package, and example calculations are included in the text.

CHAPTER 1

Introduction

One of the most striking features of vision is that despite having two eyes, one is not usually aware of two separate images of the world. Rather one sees the world as though with a single conceptual eye, referred to as the CYCLOPEAN EYE, located midway between the two real eyes.

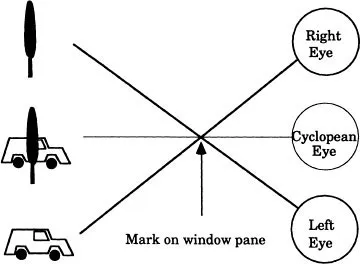
Hering (1879) introduced the idea of the cyclopean eye and provided a very simple but effective demonstration of how it works, which involves the following steps. First, stand at arm’s length in front of a window and look out with the left eye only. Select a salient feature, such as a tree and make a mark on the window, at the position of the tree. Second, look out with the right eye only, in the direction of the mark and discern a distinct feature, such as a parked vehicle, in this direction. Finally, look with both eyes open, fixating the mark on window. What one sees is the. tree and vehicle superimposed, demonstrating that the two lines of sight are merged into a common one originating at the cyclopean eye as shown in Fig. 1.1.

FIG. 1.1. Hering’s window pane demonstration. When the left eye is aligned with a tree and the right eye is aligned with a vehicle, the two images are seen in the same direction from a cyclopean eye.

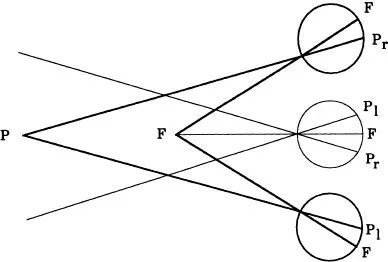
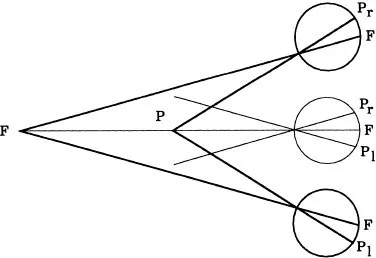
This cyclopean eye model explains the occurrence of double images that occur even with normal vision, a phenomenon known as PHYSIOLOGICAL DIPLOPIA. If two pencils are held upright and 100 millimetres apart along the straight ahead direction, then two types of diplopia can be distinguished. If the nearer pencil is fixated, as shown in Fig. 1.2, then the further pencil appears as a double image. In this and the subsequent figure, F denotes the point of fixation and P denotes the pencil which appears as a double image. Closing the left eye demonstrates that the image from the right eye appears on the right. Hence this type of physiological diplopia is referred to as UNCROSSED DIPLOPIA. If the further pencil is fixated, as shown in Fig. 1.3, then the nearer pencil appears as a double image. Closing the left eye demonstrates that the image from the right eye appears on the left. Hence this type of physiological diplopia is referred to as CROSSED DIPLOPIA.

FIG. 1.2. Demonstration of uncrossed diplopia. F is the point of fixation and P_l and P_r are the images of the point P in the left and right eye respectively.

FIG. 1.3. Demonstration of crossed diplopia.

So what is the significance of the cyclopean eye? Obviously every object could be assigned a unique visual direction with respect to a point midway between the two eyes, but this is not what the brain does and one has to look for an explanation for the phenomena in the mechanism of the nervous system.

The approach to vision science that is followed in this book is to examine the transformations of the physical stimulus which occur along the visual pathway, in order to understand what makes a given eye or brain system decide a particular way of seeing. So as to be clear about the functional implications of an eye or brain mechanism, the action of the mechanism has to be described mathematically, and the subsequent chapters of this book build on this approach.

CHAPTER 2

Vector Algebra

The most difficult part of applying mathematics to the description of a physical phenomenon involves identifying the relevant aspects of the phenomenon. This is especially true of vision, as in any natural scene, it is not obvious what constitutes the stimulus to the visual system. However, consideration of a basic visual stimulus consisting of an isolated light source, which can vary in both intensity and wavelength, makes it clear that any visual stimulus will have a number of qualitatively different aspects. The appropriate mathematical structures for describing phenomena which vary both quantitatively and qualitatively are introduced in this chapter.

Definition of Vector Properties

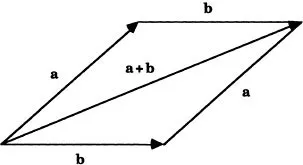
In abstract terms, a VECTOR is a quantity which specifies both the length and the direction of a translation of a point through space. By convention, vectors are denoted by boldface type, e.g. a, b, c. A simple visual representation of a vector is provided by an arrow, with the tail representing the initial position of the point and the head representing the final position of the point, after the translation. The definition of vector addition and subtraction is in keeping with the concept of a vector as a translation, in that vector addition has been defined so that it corresponds to the effect of following one translation by another. The addition is carried out according to the parallelogram rule which is readily understood from Fig. 2.1. The rule states that if two vectors a and b form the adjacent sides of a parallelogram, then their sum is represented by the diagonal from the start of one vector to the finish of the other.

Subtraction of a vector b from a vector a is defined to be equivalent to adding to a a vector of the same length as b, but with the opposite direction. This definition ensures that subtracting a vector from itself gives a zero vector.

FIG. 2.1 The parallelogram rule for vector addition

The length of a vector, which is denoted by a pair of vertical lines on either side of the capital letter, e.g. |a|, |b|, |c|, can be altered independently of the direction of the vector by multiplication by a number. The number is referred to in this context as a SCALAR to signify that it has only magnitude whilst a vector has both magnitude and direction. Hence, if s is a scalar quantity then |s a| = s |a|. In order to distinguish them from vector quantities, scalar quantities will be written in italics. ...