Investment Theory and Risk Management

Steven Peterson

• Publisher: Wiley
• Year: 2012
• Print ISBN: 9781118129593
• eBook ISBN: 9781118238417
• Edition: 1
• Topic: Business
• Subtopic: Investments & Securities
• Index: Business

A unique perspective on applied investment theory and risk management from the Senior Risk Officer of a major pension fund

Investment Theory and Risk Management is a practical guide to today's investment environment. The book's sophisticated quantitative methods are examined by an author who uses these methods at the Virginia Retirement System and teaches them at the Virginia Commonwealth University. In addition to showing how investment performance can be evaluated, using Jensen's Alpha, Sharpe's Ratio, and DDM, he delves into four types of optimal portfolios (one that is fully invested, one with targeted returns, another with no short sales, and one with capped investment allocations).

In addition, the book provides valuable insights on risk, and topics such as anomalies, factor models, and active portfolio management. Other chapters focus on private equity, structured credit, optimal rebalancing, data problems, and Monte Carlo simulation.

• Contains investment theory and risk management spreadsheet models based on the author's own real-world experience with stock, bonds, and alternative assets
• Offers a down-to-earth guide that can be used on a daily basis for making common financial decisions with a new level of quantitative sophistication and rigor
• Written by the Director of Research and Senior Risk Officer for the Virginia Retirement System and an Associate Professor at Virginia Commonwealth University's School of Business

Investment Theory and Risk Management empowers both the technical and non-technical reader with the essential knowledge necessary to understand and manage risks in any corporate or economic environment.

Chapter 1

Discount Rates and Returns

The most powerful force in the universe is compound interest.

—Albert Einstein

Estimating Returns

The total return on an investment in any security is the percentage change in the value of the asset including dividends over a specific interval of time. Assuming asset value is captured in the market price P and dividends by d, then the one period total return, r₁, is equal to

percent, in which the subscripts index time. For simplicity, we will ignore dividends, which gives us the price return, which, in decimal form, is equal to

. Thus,

is the gross return (the return plus the initial one-dollar outlay in the security) on the investment for one period, and

is the net return; it is the return on a $1 investment. We can geometrically link returns to get the time equivalent of a longer-term investment. For example, suppose that the period under study is one month and that

is therefore the one-month return. We can annualize this return by assuming the investment returns this amount in each month. Compounding this for one year is a product yielding the amount:

Here,

is the monthly return, while

is the annualized equivalent. On the other hand, we may observe a time series of past monthly returns (called trailing returns), which we geometrically link to estimate an annualized figure, that is, the previous 12 monthly returns generate an annual return given by:

We can similarly link quarterly returns to estimate an annual equivalent, for example,

, and we can do the same for weekly, daily, or any frequency for that matter, to achieve a lower frequency equivalent return. Focusing once again on monthly gross returns, annualization is a compounded return that is the product of monthly relative prices, each measuring price appreciation from the previous month, that is, by generalizing from the fact that if

, then the following must also be true:

Upon canceling, this reduces to the following, which is consistent with our definition of gross return given earlier.

This suggests that we can calculate the gross return over any period by taking the ratio of the market values and ignoring all intermediate market values. Similarly, we can solve for any intervening periodic average return by using the power rule; in this case, if the annual return is

, then the geometric average monthly return

must be

For example, the average monthly return necessary to compound to a 15 percent annual return must be approximately 1.17 percent per month:

---

Example 1.1

Quarterly returns to the Russell 3000 Domestic Equity Index for the years 2005 to 2007 are given in Table 1.1

Table 1.1 Russell 3000 Dom Eq Index

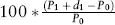
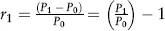
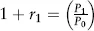
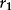
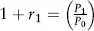
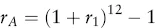
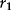
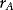
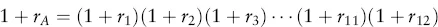
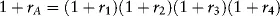
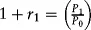
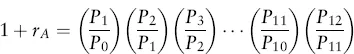
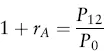
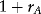
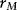
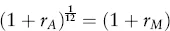
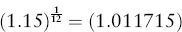
Date	Return (%)
2005Q1	–2.20
2005Q2	2.24
2005Q3	4.01
2005Q4	2.04
2006Q1	5.31
2006Q2	–1.98
2006Q3	4.64
2006Q4	7.12
2007Q1	1.28
2007Q2	5.77
2007Q3	1.55
2007Q4	–3.34

a. Geometrically link these quarterly returns to generate annual returns.

b. Calculate the return for the three-year period.

c. What is the arithmetic average annual return for these three years?

d. What is the arithmetic average quarterly return over this three-year period?

Solutions

(Refer to Table 1.2)

Table 1.2 Geometric Returns

a. Annual Return (Column E) =

b. The return for the three-year period =

; annualized, this is

geometric average.

c. The arithmetic average annual return =

.

d. The arithmetic average quarterly return =

.

Go to the companion website for more details...

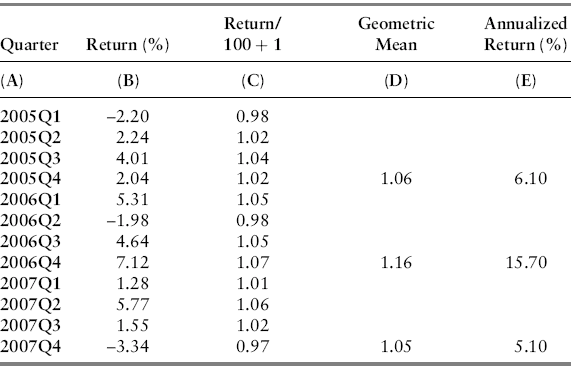
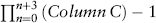
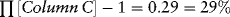
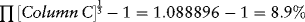
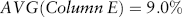
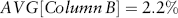
Table of contents

• Cover
• Series Page
• Title Page
• Copyright
• Dedication
• Preface
• Acknowledgments
• Chapter 1: Discount Rates and Returns
• Chapter 2: Fixed Income Securities
• Chapter 3: Term Structure
• Chapter 4: Equity
• Chapter 5: Portfolio Construction
• Chapter 6: Optimal Portfolios
• Chapter 7: Data and Applications
• Chapter 8: Anomalies
• Chapter 9: Factor Models
• Chapter 10: Active Portfolio Management
• Chapter 11: Risk
• Chapter 12: Monte Carlo Methods
• Chapter 13: Systemic Risk
• Chapter 14: Incorporating Subjective Views
• Chapter 15: Futures, Forwards, and Swaps
• Chapter 16: Introduction to Options
• Chapter 17: Models of Stock Price Dynamics
• Chapter 18: Hedging Portfolio Risk
• Chapter 19: Private Equity
• Chapter 20: Structured Credit
• Chapter 21: Optimal Rebalancing
• Chapter 22: Data Problems
• About the Author
• Index