Symmetry Discovered

Concepts and Applications in Nature and Science

Joe Rosen

• Publisher: Dover Publications
• Year: 2012
• ISBN:
  9780486145006
• Topic: Tecnología e ingeniería
• Subtopic: Ciencias aplicadas

Symmetry provides an insight into the way nature works and is often used by scientists and technologists to help solve problems. Symmetry has numerous other applications as well — with more being discovered all the time in science, the arts and other fields of human endeavor.
This classic work provides an excellent introduction to the basic concepts and terminology (including, optionally, group theory), as well as lucid discussions of geometric symmetry, other symmetries and appropriate symmetry, symmetry in nature, uses of symmetry in science and much more.
Readers wishing to pursue specific topics will find many references that reflect the author's wide reading in the subject and his own obvious enthusiasm. For this edition, Dr. Rosen has provided a new preface, solutions to the problems, and an addendum to the bibliography.

3

Geometric symmetry

Geometric symmetry is symmetry with respect to geometric transformations. A geometric transformation is any transformation that affects only the geometric properties of a system. This is the kind of symmetry that is usually alluded to, when the word ‘symmetry’ is mentioned in everyday conversation. It is then related to features such as balance, regularity, order, repetition, proportionality, harmony and similarity. As we emphasized in the first chapter, the concept of symmetry is much broader and more general than just geometric symmetry. But geometric symmetry is obviously important, and it is well worth our while to increase our understanding of it. This is what we attempt to accomplish in the present chapter. References are listed under GEO in the bibliography, including cross-references.

The space with which we are familiar, in which we live, objects exist and events occur, is 3-dimensional. All real systems are 3-dimensional, and geometric transformations can affect them 3-dimensionally. Abstract systems having geometric properties, though, do not have to be 3-dimensional, but can be 2- or 1-dimensional. (As long as they are abstract, they can even be 4-dimensional or n-dimensional, but we do not concern ourselves with these here.) The square of chapter 1, for example, has no thickness and so is a 2-dimensional system. And even real systems might be considered as being 2- or 1-dimensional, when one or two of their dimensions can be ignored for the purposes of the discussion. For instance we can treat a length of pipe as a 1-dimensional system, if we are only interested in symmetries related to its longitudinal dimension. But we can also think of the same length of pipe as a 2-dimensional system, if we are only investigating the shape of its cross-section. It is convenient to consider separately the geometric symmetries of 1-, 2- and 3-dimensional systems. We refer to these respectively as linear, planar and spatial symmetry.

Linear symmetry

Winnie-the-Pooh read the two notices very carefully, first from left to right, and afterwards, in case he had missed some of it, from right to left.

(A.A. Milne: Winnie-the-Pooh)

The geometric transformations that we discuss for 1-dimensional systems are displacement and plane reflection.

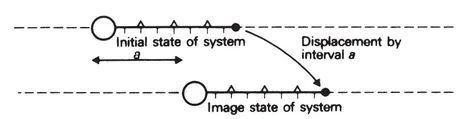
Fig. 3.1
Displacement transformation of 1-dimensional system

The transformation of displacement (or translation) involves displacing the system by a given interval in the only direction that the system is considered to have (fig. 3.1). A system can be symmetric under displacement only if it is of infinite extent and so has no ends.

Fig. 3.2
Displacement symmetric 1-dimensional systems

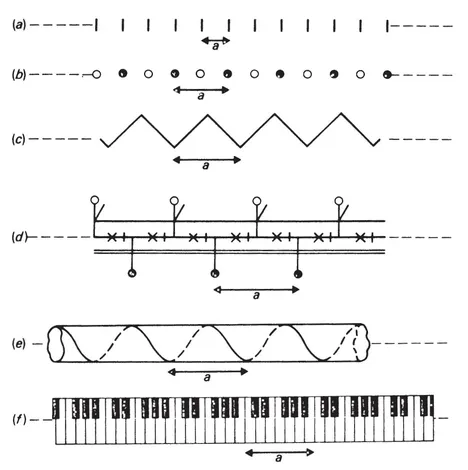
An infinite straight line is symmetric under displacements by any interval in the direction of the line (fig. 3.2(a)). So too is an infinite straight rod of constant diameter (fig. 3.2(b)). Any system that has an infinite regular repetition in one direction is symmetric under displacements in that direction, but only under those displacements by a certain minimum displacement interval and multiples of it. The patterns of fig. 3.3 are examples of such systems. The minimum displacement interval is denoted by a in each case.

No real system is infinite, however, so no real system can have exact displacement symmetry. But a finite system is said to have approximate displacement symmetry, if it can be imagined as being part of an infinite exactly symmetric system and if the minimum displacement interval is much smaller than the total length of the system. Then we can ignore the effect of the ends, as long as we observe the system sufficiently far from the ends and restrict the displacements to sufficiently small multiples of the minimum displacement interval.

Fig. 3.3
Displacement symmetric 1-dimensional systems with minimum displacementintervals indicated by a

Systems with approximate linear displacement symmetry occur in everyday situations. Some examples are: a long traffic jam, a long train, railroad tracks and their cross-ties, a large pile of data processing cards, telephone poles along a highway, cracks (the ones put in on purpose) along a sidewalk.

Group theory. The set of all displacements along a line, including the identity transformation, with the composition of consecutive displacement, forms a commutative group of infinite order, called the continuous linear displacement group. Among these transformations any set consisting of the identity transformation and displacements by all multiples of any minimum displacement interval form a subgroup, also of infinite order, a discrete linear displacement group. All such subgroups are isomorphic.

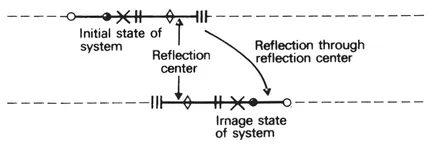
The plane reflection (or plane inversion) transformation is accomplished by imagining a mirror with its plane perpendicular to the direction of the system and reflecting the system in it. The intersection of the mirror with the line of the system is called the reflection center. The image of a point falls therefore on the line of the system, on the opposite side of the reflection center from the initial point, and at the same distance from the reflection center as is the initial point (fig. 3.4). Reflection transformations through different centers do not commute. Both finite and infinite systems can have reflection symmetry.

Fig. 3.4
Plane reflection transformation of 1-dimensional system

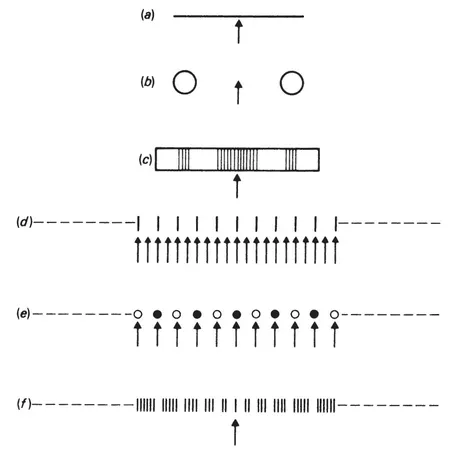
A line segment has reflection symmetry through a center located at its middle (fig. 3.5(a)). An infinite straight line is symmetric under reflection through any center located anywhere along the line (fig. 3.2(a)). Fig. 3.5 presents examples of reflection symmetric patterns. Centers of reflection symmetry are indicated by arrows. The systems of fig. 3.3(d), (e) do not have reflection symmetry, while those of fig. 3.3(a)–(c), (f) do.

PROBLEM

Find the centers of reflection symmetry for the reflection symmetric patterns of fig. 3.3.

Note that if a displacement symmetric system also has plane reflection symmetry, then it has an infinite number of centers of reflection symmetry separated by half the minimum displacement interval. This is shown in fig. 3.5(d), (e).

Fig. 3.5
Plane reflection symmetric 1-dimensional systems with centers of reflection symmetry indicated by arrows

PROBLEM

Why is this so?

A common example of a 1-dimensiona...

Table of contents

• Title Page
• Copyright Page
• Table of Contents
• Dedication
• Foreword
• Preface
• Preface to the Dover Edition
• I - Symmetry: what? where? how?
• 2 - The language of symmetry
• 3 - Geometric symmetry
• 4 - Other symmetries and approximate symmetry
• 5 - Symmetry in nature
• 6 - Uses of symmetry in science
• Conclusion
• Bibliography
• Addendum to the Bibliography
• Solutions to Problems
• Index