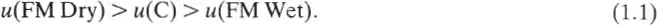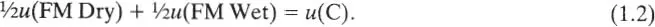Games, Theory and Applications

L. C. Thomas

• Publisher: Dover Publications
• Year: 2012
• ISBN:
  9780486143736
• Topic: Mathematik
• Subtopic: Spieltheorie

Anyone with a knowledge of basic mathematics will find this an accessible and informative introduction to game theory. It opens with the theory of two-person zero-sum games, two-person non-zero sum games, and n-person games, at a level between nonmathematical introductory books and technical mathematical game theory books. Succeeding sections focus on a variety of applications — including introductory explanations of gaming and meta games — that offer nonspecialists information about new areas of game theory at a comprehensible level. Numerous exercises appear with full solutions, in addition to an extensive bibliography, 80 problems with worked solutions, and over 30 illustrations useful for the theory of non-zero and n-person games. 1986 edition.

CHAPTER 1

‘The game’s afoot’

(Shakespeare)

1.1 WHAT IS A GAME?

Have you read the newspaper today? If so, the front page probably contains a report of some political controversy, or a strike, or perhaps describes armed conflict and violent actions by groups of people or countries. The inside pages will report actions by various pressure groups to change social policy, or will describe government decisions about such policies—improvements in housing, allocation of finance to the various branches of health and social services. The financial pages will be full of take-overs, firms’ attempts to improve their market share, changes in prices of goods, or government attempts to control the financial markets. Finally, there will be the sports page or the chess or bridge column to read.

What do all these reports have in common? They all describe conflicts of interests between people or groups of people such as political parties, governments, and businesses. We call the theoretical models of such conflicts of interests games. Recalling the famous definition of a model as a small imitation of the real thing (as in ‘model husband’) indicates that in a game one is trying to extract the essential problems in the conflict of interest. Game theory consists of ways of analysing these problems. Obviously, most conflicts are too complicated to include all the facets involved in the corresponding model, but a game could still be useful in describing the main types of decisions open to the participants and the sort of results that could occur. For some games, game theory will suggest a ‘solution’ to the game, that is a best way of playing the game for each person involved; but for most games describing real problems all it can do is to rule out some types of decisions and perhaps suggest, which players will work together.

These theoretical models of conflict are called games because we can identify easily the conflicts of interest in recreational games like Poker, Noughts and Crosses, or Monopoly; and some of the board games, like Chess, did develop historically as models of warfare. It is in a way an unfortunate choice of name, because it has the connotations of amusement, light-heartedness, and a recreational contest. I hope the reader will occasionally be amused, but games cover a much wider area than just board games or ‘bored’ games. We shall consider economic and business problems, the tactics and logistics of warfare, international and national politics, and social policy all as candidates to be modelled as games.

1.2 EXAMPLES OF GAMES

To get a feeling for what is involved in a game, let’s look at some simple examples. Try to think what are their important features and what if anything they have in common.

Example 1.1 — Noughts and Crosses. Draw an n × n grid. The first player puts a nought in any square, and then the second player puts a cross in some unused square. Continue in sequence until one player has a line (column, row, or diagonal) of n noughts or n crosses. That player then wins.

You probably haven’t played this game for a few years, so now is your chance. You will find that if n = 1 or 2, the first player always wins, and if n = 3, you can always draw unless you make a mistake. What happens for n = 4 and higher n? What about the three-dimensional version, i.e. n × n × n?

Example 1.2—Simplified Poker. There are only two cards involved—an ‘Ace’ and a ‘Two’—and only two players—whom we label I and II. Each puts £1 in the pot and I deals II one card, which II then looks at. If it is the Ace, II must say ‘Ace’, but if it is the ‘Two’, II can say ‘Ace’ or ‘Two’. If he says ‘Two’ he loses the game and his £1 in the pot. If, however, II says ‘Ace’ no matter what the card is, II must put another £1 in the ‘pot’. In this case player I can either believe him, i.e. ‘fold’ and so lose his £1 in the ‘pot’, or else he can demand to ‘see’ the card. In this case I has to put another £1 into the pot, and then the card is shown. If II had the Ace he wins the ‘pot’ and so takes £2 from I, but if II has the Two, I wins the ‘pot’ and so takes £2 from II. This game involves the elements of ‘bluffing’ and ‘calling’ involved in real poker, but not surprisingly has not yet taken Las Vegas by storm.

Example 1.3 — Nim. A number of matches are set out in two piles, and two players take turns at taking matches from the piles. At each turn a player must take at least one match, but he can take more provided they are all from the same pile. The loser is the player who picks up the last match.

Example 1.4—Prisoners’ Dilemma. Two people, arrested with stolen property in their possession, are being interviewed separately by the police. They both know that if they keep quiet there is not enough evidence for them to be convicted of theft, and so they will only get a one-year gaol sentence for being in possession of stolen property. If both confess to the theft, they will both get nine years in prison. However, if one confesses and the other keeps quiet, the one who turned Queen’s Evidence will go free, while the other will have a ten-year gaol sentence (the extra year is for not assisting the police). What should they do? Would it make any difference if they could talk to each other between being arrested and interviewed? You can argue that this game also embodies the dilemma over nuclear disarmament or whether unions should pursue high or low wage claims for their members. Can you see why?

Example 1.5—Pick a number. Each person in a group of people chooses a number. The one with the highest number wins. What number would you choose? Infinity is not allowed. Could you guarantee to win the game somehow?

Example 1.6—Duellists. Two duellists stand 2N paces apart with loaded pistols and start to walk toward each other. At each pace they can decide whether or not to fire their one bullet, and the chance of killing their opponent increases as they get nearer. If they fire and miss, honour demands that they still keep walking nearer. When should each man fire? Is this affected by whether their aim [sic] is to kill their opponent or to stay alive themselves? In a duel, you would know when your opponent had fired and missed, but suppose instead you were in planes, far apart, armed with a missile, so you didn’t know if your opponent had fired and missed. Would this make any difference to when you should fire?

1.3 TERMINOLOGY OF GAME THEORY

Let us emphasise again that game theory is not a prescriptive way of how to play a game. Rather it is a set of ideas and techniques for analysing these mathematical models of conflict of interest. It doesn’t tell you how to play the game, but describes properties that certain ways of playing the game have, and which you might think desirable. Even when the analysis suggests a best way of playing the game, it only does it assuming that everyone is playing in the ‘best way’ they can. It never allows for ways of punishing your opponent if he makes a mistake, which is the way most games, whether board ones or real life conflict situations, end.

Before we start on this analysis let us look again at the six examples in the previous section, and see what features they have in common. This will help us in defining the terminology of game theory.

Firstly there are always at least two participants (as many as you like in Example 1.5) called the players hereafter labelled I, II, III, etc. or, in later chapters, 1, 2, 3, etc. Each game consists of a sequence of moves, some simultaneous, which are either decisions by the players or outcomes of chance events. Thus, in the simplified poker of Example 1.2 the first move is the chance event of which card is picked. If it is a Two, this is followed by the decision by II whether to say ‘Ace’ or ‘Two’. If II says ‘Ace’, the last move is whether I believes him or not.

At the end of the game, each player receives a payoff. We will always assume that the payoff is given by a real number. In many games you could associate this number with the amount won, or say the payoff is +1 if you won the game, 0 if it is a draw, and –1 if you lose it. However, in other games the result is more complicated or intangible.

When von Neumann and Morgenstern (1947) introduced the basics of game theory, they also developed the idea of the utility of an outcome of the game, so that these numbers reflect your preferences. Thus, suppose the outcomes of the game were ‘going to a football match’ or ‘going to the cinema’ and you preferred the football match. You would choose two numbers u(FM)—the utility of going to the football match—and u(C)—the utility of going to the cinema—so that u(FM) > u(C). Say u(FM) = 4, u(C) = 2. Obviously you can choose almost any pair of numbers here, but if you start asking more of the utility function this cuts down the number of possible numerical representations. Thus, you may prefer seeing the football match in the dry, to going to the cinema; but would rather go to the cinema than get soaked watching a football match. This requires the utilities to satisfy

If you think the chance of rain tonight is ½, and you can’t decide whether to go to the football match or the cinema (you are indifferent) this would be represented by the equation

Thus, if you choose u(FM Dry) = 4, u(C) = 2, this means u(FM Wet) must equal 0. This is the situation in most versions of utility theory, where you can choose the utility of two outcomes as you like, provided they reflect your preference, but the utilities of all the other outcomes are then fixed completely by your preferences. Readers who want to learn more about utility theory and the axioms underlying it should turn to Chapter 2 of Luce and Raiffa (1957) or to Raiffa (1968).

We will always assume that the players’ preferences over the outcomes of a game satisfy the rules underlying utility theory, and so each outcome can be represented numerically by its utility value. Remember that this utility reflects all the aspects of the outcome, including your regret or joy about what happened to your opponent. So if you get a payoff of utility value 4 and your opponent gets one of 2, you are as happy with that as if you get 4 and he gets 200 or –200.

Returning to the common features in the various games, notice that each player has to make decisions at some moves of the game. A strategy for a player is a description of the decisions he will make at all the possible situations that can arise in the game. Thus, having chosen his strategy it will tell him what to do at every situation that can arise no matter what his opponent does or what are the outcomes of the chance events. In 2 × 2 Noughts and Crosses, a strategy tells the first player which of the four squares to put his first nought in; and for each of the three replies by his opponent it must say which of the remaining two squares to put the second nought in. Think of it as a set of instructions which enables a computer to play the game for you. It is obvious that for many games, chess for instance, although in principle you can conceive of a strategy, in practice it is too long to write down. (If you were ‘Black’ in chess you would have to write down your response to all 20 possible opening moves by White, and at your second move reply to all the 400 different situations White can be in after two moves, and so on.)

If the sum of the players’ payoffs is zero no matter what st...

Table of contents

• Cover
• Title Page
• Copyright Page
• Dedication
• Contents
• Author’s Preface
• Glossary of Symbols
• Chapter 1 ‘The Game’s Afoot’
• Chapter 2 Two-Person Zero-Sum Games
• Chapter 3 Two-Person Non-Zero-Sum Games
• Chapter 4 N-Person Games
• Chapter 5 Market Games and Oligopoly
• Chapter 6 Metagames
• Chapter 7 Multi-Stage Games
• Chapter 8 Evolutionary Games
• Chapter 9 Bidding and Auctions
• Chapter 10 Gaming
• Solutions to problems
• References
• Index
• Name index