Geometric Magic Squares

A Challenging New Twist Using Colored Shapes Instead of Numbers

Lee C.F. Sallows

• Publisher: Dover Publications
• Year: 2013
• ISBN:
  9780486290027
• Topic: Mathematics
• Subtopic: Games in Mathematics
• Index: Mathematics

Traditional magic squares are squares of numbers in which the rows, columns, and diagonals all add up to the same total. With a voluminous literature going back some 2, 500 years, the universal assumption has ever been that magic squares are inherently arithmetical objects. In this innovative work by a British engineer, the author initiates a Copernican revolution in our understanding by replacing numbers with two-dimensional forms. The result is not merely a novel kind of geometrical magic square but a revelation that traditional magic squares are now better seen as the one-dimensional instance of this self-same geometrical activity.

Part I

Geomagic Squares of 3×3

There is mystery in symmetry. With an m to spare.

1 Introduction

I expect most readers will be familiar with the traditional magic square: a chessboard-like array of cells in which numbers, usually but not always consecutive, are written so that their totals taken in any row, any column, or along either diagonal, are alike. Figure 1.1 shows the best known example of size 3×3, the smallest possible, a square of Chinese origin known as the Lo shu. The constant sum of any three entries in a straight line is 15. The diagram at left shows the Lo shu in traditional form, an engaging device nowadays identified by sinologists as a pseudo-archaic invention of the 10th century A.D.; see Cammann[1]. The dot-and-line notation was intended to suggest an origin of extreme antiquity.

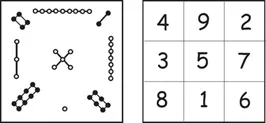
Fig. 1.1 The Lo shu.

The history of magic squares is a venerable one, earliest writings on the topic dating from the 4th century BC[2]. Abstruse as they may appear, these curiosities have long exercised a peculiar fascination over certain minds, attracting over the centuries a steady following of devotees, by no means all of them mathematicians. As Martin Gardner has written, “The literature on magic squares in general is vast, and most of it was written by laymen who became hooked on the elegant symmetries of these interlocking number patterns.”

It is true. I myself am such a layman; a mathematical amateur with an irrational fondness for the crystalline quality of these numerical prisms (see, for example, [3] and [4].) But with that humble position owned up to, my purpose in the present essay is in fact decidedly less timid.

My thesis is that the magic square is, and has ever been, a misconstrued entity; that for all its long history, and for all its vast literature, it has remained steadfastly unrecognised for the essentially non-numerical object it really is. Just as a cylinder may be mistaken for a circle when observed from a single viewpoint, so may a familiar object turn into something quite unexpected when seen from a new perspective. In a similar vein, I suggest the numbers that appear in magic squares are better understood as symbols standing for (degenerate instances of) geometrical figures. Hence the prefix geometric to distinguish the wider genus of magic square that will turn out to include the old species within it. For, as we shall see, the traditional magic square is really no more than that special instance of a geometric magic square in which the entries happen to be one-dimensional. But once we are introduced to squares using two-dimensional entries the scales fall from our eyes and we step into a wider, more exhilarating world in which the ordinary magic square occupies but a humble position.

2 Geometric Magic Squares

Consider a graphical representation of the Lo shu as seen in Figure 2.1 at right, in which straight line segments of length 1, 2 ,3, … replace like-valued numbers in each cell. The orientation of these segments in their cells is unimportant; they may be horizontal, vertical, or slanted at any angle. The constant sum, 15, as represented by 8+1+6 in the bottom row, say, then becomes three segments of length 8, 1, and 6 that are joined head to tail so as to form a single straight line of length 15.

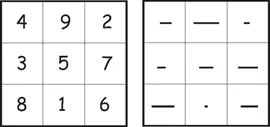
Fig. 2.1 A geometrical version of the Lo shu.

We note that the order in which 8, 1, and 6 are abutted is non-critical, the important thing being only that they fit together end-to-end so as to fill or ‘pave’ a straight line of length 15. And similarly for the seven other sets of three line segments occupying the remaining rows, columns, and main diagonals, collectively known as ‘magic lines.’ Hence more generally:

(1) The numbers that occur in magic squares can be seen as abbreviations for their geometrical counterparts, which are straight line-segments of appropriate length.

(2) The process of adding numbers so as to yield the recurring constant sum is then easier to interpret as the arithmetical counterpart of partitioning or tiling a space with these line segments.

The advantage of this view now emerges in an entirely novel contingency it immediately suggests. For just as line segments can pave longer segments, so areas can pave larger areas, volumes can pack roomier volumes, and so on up through higher dimensions. In traditional magic squares, we add numbers so as to form a constant sum, which is to say, we ‘pave’ a one-dimensional space with one-dimensional ‘tiles.’ What happens beyond the one dimensional case?

Geometric or, less formally, geomagic is the term I use for a magic square in which higher dimensional geometrical shapes (or tiles or pieces) may appear in the cells instead of numbers. For the moment we shall dwell on flat, or two-dimensional shapes, although non-planar figures of 3 or higher dimensions may equally be used. The orientation of each shape within its cell is unimportant. Such an array of N × N geometrical pieces is called magic when the N entries occurring in each row, each column, as well as in both main diagonals, can be fitted together jigsaw-wise to produce an identical shape in each case. In tessellating this constant region or target, pieces are allowed to be flipped. As with numerical, or what I now call numagic squares, geomagic squares showing repeated entries are denoted (and deemed) trivial or degenerate, which are terms we shall have need of more often. Rotated or reflected versions of the same geomagic square are counted identical, as are rotations and reflections of the target. A square of size N × N is said to be of order N. We say that a geomagic square is of dimension D when its constituent pieces are all D-dimensional. This is an informal introduction to geomagic squares; for a formal definition see Appendix I. In the following, our concern will be almost exclusively with 2-D, or two-dimensional squares.

Figure 2.2 shows a 3×3 two-dimensional geomagic square in which the target is itself a square. Any 3 entries in a straight line can be assembled to pave this same square-shape without gaps or overlaps, as illustrated to right and below. Note how some pieces appear one way in one target, while flipped and/or rotated in another. Thin grid lines on pieces within the square help identify their precise shape and relative size.

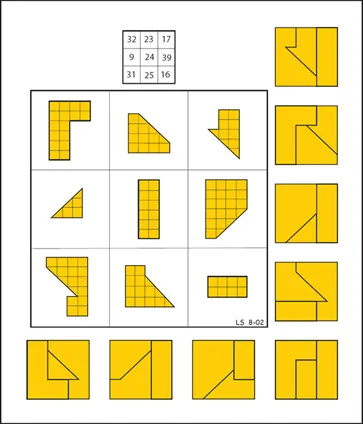
Fig. 2.2 A 3 × 3 geomagic square.

At the top is a smaller 3 × 3 square with numbers indicating the areas of corresponding pieces in the geomagic square, expressed in units of half grid-squares. Since the three pieces in each row, column, and diagonal tile the same shape, the sum of their areas must be the same. This is, therefore, an ordinary numagic square (or one-dimensional geomagic square) with a constant sum equal to the target area. Analogous area squares for many geomagic squares are often degenerate because differently shaped pieces may share equal areas.

The concept of geometric magic squares grew out of an original impulse to create a pictorial representation of the algebraic square shown in Figure 2.3, a formula due to the 19^th century French mathematician Édouard Lucas[5] that describes the structure of every 3×3 numagic square. The Lo shu, for example, is that instance of the formula in which a = 3, b = 1, and c = 5. From here on the terms formula and generalization will be used interchangeably.

The idea unde...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Dedication
• Foreword
• Part I: Geomagic Squares of 3×3
• Part II: Geomagic Squares of 4×4
• Part III: Special Categories
• Appendix I. A Formal Definition of Geomagic Squares
• Appendix II. Magic Formulae
• Appendix III. New Advances with 4×4 Magic Squares
• Appendix IV. The Dual of the Lo shu
• Appendix V. The Lost Theorem
• Glossary
• References