Applied Matrix Algebra in the Statistical Sciences

Alexander Basilevsky

• Publisher: Dover Publications
• Year: 2013
• ISBN:
  9780486153377
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

This comprehensive text covers both applied and theoretical branches of matrix algebra in the statistical sciences. It also provides a bridge between linear algebra and statistical models. Appropriate for advanced undergraduate and graduate students, the self-contained treatment also constitutes a handy reference for researchers. The only mathematical background necessary is a sound knowledge of high school mathematics and a first course in statistics.
Consisting of two interrelated parts, this volume begins with the basic structure of vectors and vector spaces. The latter part emphasizes the diverse properties of matrices and their associated linear transformations--and how these, in turn, depend upon results derived from linear vector spaces. An overview of introductory concepts leads to more advanced topics such as latent roots and vectors, generalized inverses, and nonnegative matrices. Each chapter concludes with a section on real-world statistical applications, plus exercises that offer concrete examples of the applications of matrix algebra.

Chapter 1

Vectors

1.1 Introduction

In applied quantitative work matrices arise for two main reasons—to manipulate data arranged in tables and to solve systems of equations. A real matrix A is defined as a n × k rectangular array

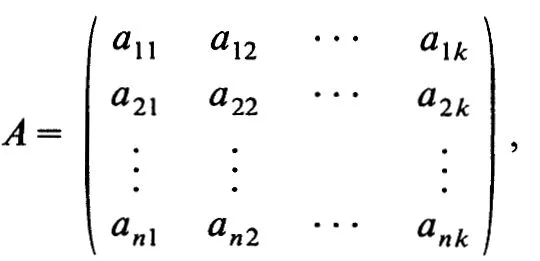
where the real a_ij (i = 1, 2,..., n; j = 1, 2,..., k) comprising the elements of A have either known or unknown values. When n = 3 and k = 2, we have the 3 × 2 matrix

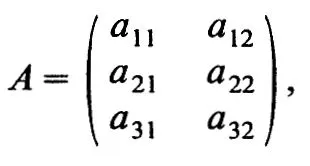
and when the elements are known we may have, for example,

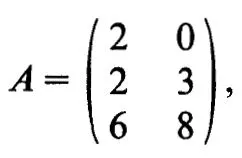
where a₁₁ = 2, a₁₂ = 0,..., a₃₂ = 8. The subscripts i and j are convenient index numbers that indicate the row and column of a_ij, respectively. For the special case when n = k =1, matrix A reduces to a single number, referred to as a scalar. When n = 1 (k =1) we obtain a row (column) array, or a vector, which can be viewed as a particular type of matrix. Alternatively, a matrix can be considered as a set of vectors, which in turn consist of real scalar numbers. Each view has its own particular merit, but for the sake of exposition it is useful to first consider properties of vectors and to then extend these properties to matrices. Geometrically, a vector is represented as a point in a Cartesian system of coordinate axes and is frequently depicted by a straight arrow (Figure 1.1); however, it is important to keep in mind that a vector is in fact a point, and not a straight line.

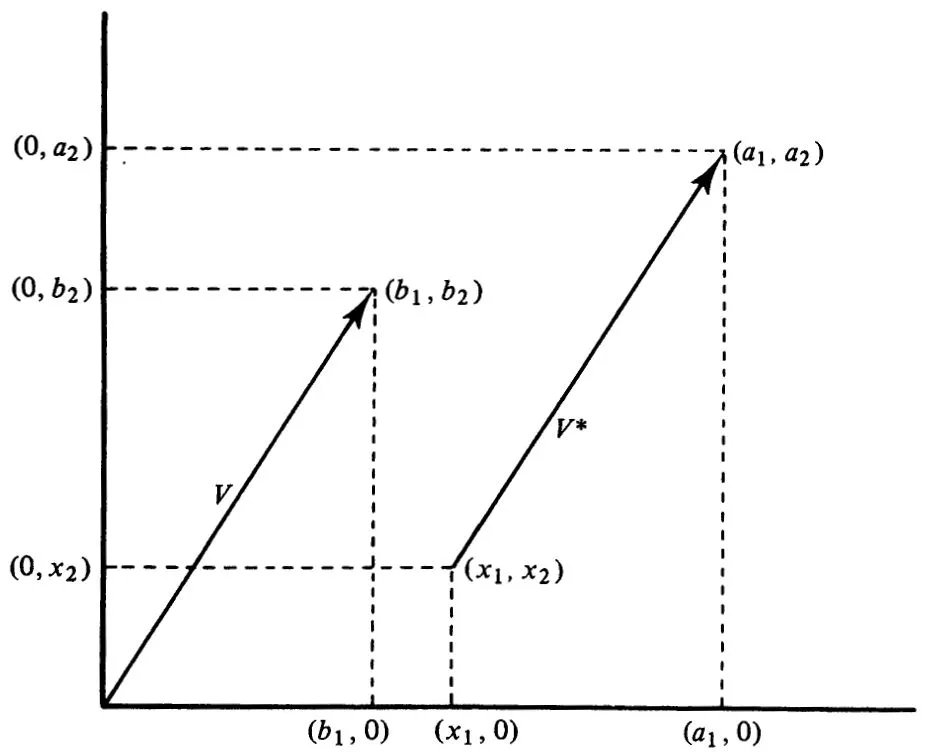
Figure 1.1 A parallel translation of a vector V to a new location V

1.2 Vector Operations

Although geometric representations of vectors can be intuitive aids and will be used frequently in the following chapters, they are less helpful for defining the basic properties of vectors, which is best achieved by algebra.

Let a set of n numbers a_i (i = 1, 2, ...,n), be represented in the linear¹ array (a₁, a₂,...,a_n) where, in general, interchanging any two (or more) numbers results in a different set. The set (a₂, a₁,..., a_n), for example, is not the same as a₁, a₂,...,a_n), unless a₁ = a₂. For this reason a vector is said to be ordered. Such ordered sets of numbers are generally referred to a...

Table of contents

• DOVER BOOKS ON MATHEMATICS
• Title Page
• Copyright Page
• Dedication
• Table of Contents
• Preface
• Chapter 1 - Vectors
• Chapter 2 - Vector Spaces
• Chapter 3 - Matrices and Systems of Linear Equations
• Chapter 4 - Matrices of Special Type
• Chapter 5 - Latent Roots and Latent Vectors
• Chapter 6 - Generalized Matrix Inverses
• Chapter 7 - Nonnegative and Diagonally Dominant Matrices
• References
• Index