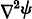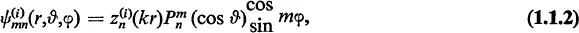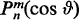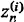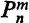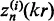Spheroidal Wave Functions

Carson Flammer

• Publisher: Dover Publications
• Year: 2014
• Print ISBN: 9780486446394
• eBook ISBN: 9780486158518
• Topic: Mathematics
• Subtopic: Functional Analysis
• Index: Mathematics

Intended to facilitate the use and calculation of spheroidal wave functions, this applications-oriented text features a detailed and unified account of the properties of these functions. Addressed to applied mathematicians, mathematical physicists, and mathematical engineers, it presents tables that provide a convenient means for handling wave problems in spheroidal coordinates.
Topics include separation of the scalar wave equation in spheroidal coordinates, angle and radial functions, integral representations and relations, and expansions in spherical Bessel function products. Additional subjects include recurrence relations of Whittaker type, asymptotic expansions for large values of c, and vector wave functions. The text concludes with an appendix, references, and tables of numerical values.

1

introduction

1.1 Historical Survey

The differential equations resulting from the separation of the scalar Helmholtz differential equation

in general ellipsoidal coordinates, were first obtained in the case of k² = 0, i.e., for the Laplace equation, by G. Lamé [l]¹ in 1837. This was three years after Lamé had for the first time effected the transformation of

to general orthogonal coordinates [2]. Consequently the designation of ‘Lamé’s equation’ came into use, and the integrals of the separated differential equations became known as ‘Lamé’s functions.’ Later, as the wave equation with k² > 0 came under consideration, the designations ‘Lamé’s potential functions,’ or ellipsoidal harmonics, and ‘Lamé’s wave functions’ were used for distinction.

For general ellipsoidal coordinates, Lamé’s wave functions have not been investigated very thoroughly. The most extensive investigation to date is that of Möglich [3], who has cast the integrals of the differential equations into the form of solutions of certain homogeneous integral equations, and thereby ascertained results of a general nature. Möglich’s general formulation does not, however, lend itself readily to numerical evaluation in its present form. Because of their greater tractability, more consideration has been given to the wave functions in the degenerate cases which result when two of the three ellipsoidal axes become equal in length, that is, in the prolate and oblate spheroidal coordinate systems. These functions are generally called spheroidal wave functions.

In the following paragraphs we shall outline more or less chronologically the main contributions to the development of spheroidal wave functions. Some acquaintance with the subject matter of the chapters succeeding this one is required, unfortunately, for an understanding and appreciation of the remainder of this section. The following parenthetic remarks may however be helpful in alleviating some of the difficulty. It is assumed that the reader is acquainted with the separation of eq.(1.1.1) in spherical coordinates (r,ϑ, < p). The eigenfunctions which are single-valued and are finite at the poles of the sphere have the form

where m and n are integers. The functions

are the associated Legendre functions of the first kind, and the

for i = 1, 2, 3, and 4 are the spherical Bessel, Neumann, Hankel functions of the first and second kinds.² In the spheroidal coordinate systems shown in Figs. 1 and 2 and defined by eqs.(2.1.1) and (2.1.2) of Chapter II, the eigenfunctions of eq.(1.1.1) will have the form of eq.(1.1.2) with the functions

replaced by functions of the ‘radial’ spheroidal coordinate ξ, and the functions

replaced by functions of the ‘angle’ coordinate η. These functions of ξ and of η will be called the radial and angle spheroidal functions, respectively. The differential equations satisfied by these functions are given in eqs.(2.2.6) to (2.2.8). Now as the eccentricity of a spheroid goes to zero, the spheroid becomes a sphere in the limit. Consequently the spheroidal wave functions reduce to the spherical wave functions in the limit of zero eccentricity.

The first investigation of the spheroidal wave functions was made by Niven [4] in 1880 in order to treat a problem on the conduction of heat in spheroidal bodies. Niven introduced series of Legendre functions for the angle spheroidal functions and series of spherical Bessel functions for the radial spheroidal functions. The numerical values of the coefficients in the series developments calculated by Niven contain, however, several errors which unfortunately were taken over into the monograph by Strutt [5]. A somewhat more extensive investigation, with several applications, was made by Maclaurin [6] in 1898, who introduced power-series solutions for the spheroidal wave functions. Some integral representations for the spheroidal functions were introduced by Abraham [7] in 1899, who studied the free oscillations of a prolate spheroid. Much later, in 1923, Poole [8] made a more extensive investigation of the most important integral relations. Other integral representations were obtained by Möglich [1\] in 1927 as the degenerate form of his general results on the ellipsoidal functions mentioned above. The monograph by Strutt [5], published in 1932, contains a survey of some of the work mentioned in this paragraph, along with an extensive bibliography of the work up to that time.

So far, the discussion has tacitly referred to solutions of the Helmholtz equation(l.l.l) in which the wave number is spatially independent. But Schrödinger′s equation

for the quantum mechanical two-center problem, of which the problem of the hydrogen molecule-ion is a particular case, is also separable in prolate spheroidal coordinates with foci at the nuclei. When the nuclei are equal, the equation in the angle coordinate for the bound states is identical with that satisfied by the oblate angle functions (oblate rather than prolate because of the negative energy); the equation in the radial coordinate differs, however, from that satisfied by the radial functions. The problem with equal nuclei was first treated by Wilson [9] in 1928. In addition to solutions for the angle functions in terms of simple power series and in series of Legendre functions, Wilson proposed a third type of solution for the case of large values of the occurring parameter (proportional to the energy). Wilson’s discussion of the latter solution was amended by Jaffe [10] in 1934; superior solutions for this case were given later by Baber and Hasse [11] in 1935 and by Svartholm [12] in 1938. The radial equation was treated by Teller [13] in 1930, by Hylleraas [14] in 1931, and also by Jaffe and by Svartholm. The problem was treated by Chakravatary [15] in 1939, who criticized the work of most of the forenamed authors. Additional details were furnished by Sandeman [16] in 1935, by Steensholt [17] in 1936, by Fisher [18] in 1937, and by Johnson [19] in 1941.

Another quantum mechanical problem, the Ramsauer effect in the case of symmetric diatomic molecules, was treated by Stier [101] in 1932 with the aid of spheroidal wave functions. Upon assuming a prolate spheroidal shape for the molecule and a suitable form for the internal potential function, Stier calculated by the method of partial waves the scattering of the plane wave of free electrons incident on the molecule. Stier employed solutions of the type introduced by Niven and computed power-series expansions of the expansion coefficients and other relevant quantities.

The further developments of the subject have been made with a view toward the application of the spheroidal wave functions in acoustical and electromagnetic boundary value problems. Integral representations were employed by Kotani [20] in 1933 who furnished some new details. Hanson [21] in 1934 studied expansions in Legendre and spherical Bessel functions and committed the error for the first time of obtaining a second solution of the angle equation by simply replacing the Legendre functions of the first kind by those of the second kind. In 1935 Stratton [22] commenced his investigations of the spheroidal functions by means of expansions in Gegenbauer functions. At the same time Morse [23] derived various integral and addition formulas for the Stratton functions. In 1941 Chu and Stratton [24] presented an extensive analysis of the spheroidal functions, couched for the most part in expansions of Gegenbauer functions. These authors presented suitably normalized functions defined by series of Legendre and spherical Bessel functions. They gave for the first time the correct expansions for the functions defined by series of Legendre functions of the second kind. This was also done almost simultaneously in 1941 by Bouwkamp [25] in treating the acoustical diffraction by a circular aperture. Bouwkamp also presented an improved method for calculating the eigenvalues and expansion coefficients, developed later independently by Blanch [26], as well as calculating several numerical details pertaining to the oblate wave functions of order zero. In the same year the work of Chu and Stratton was combined with a collection of formulas, describing the important mathematical properties of the functions, and a set of tables of eigenvalues and expansion coefficients into the well-known treatise of Stratton, Morse, Chu, and Hutner [27].

In 1944 Meixner [28] gave an analysis of the spheroidal functions which included some initial work on asymptotic forms of the functions and eigenvalues for large values of the parameter, c, equal to the product of the wave number and the semi-focal distance. The latter was based, in part, upon previous work noted above on the quantum mechanical two-center problem. Further details were given by Meixner [29, 30] in 1947 and 1948. The asymptotic series for the eigenvalues of the prolate functions were reproduced independently by Eberlein [31] in 1948. Rigorous treatments of asymptotic expansions of the spheroidal eigenvalues and eigenfunctions were given by Sips [32] and by Abramowitz [33] in 1949.

The prolate spheroidal wave functions were discussed by Page [34] in 1944 from the viewpoint of using simple power series at small arguments. The same viewpoint was adopted later by Spence [35] in 1948 and by Leitner and Spence [36] in 1950 for treating the oblate spheroidal wave functions. These authors extended the tabulation of the eigenvalues and presented some numerical values of the angle functions. Calculations of the radial as well as the angle prolate functions were made by Spence [37]. Power-series expansions of the Stratton prolate functions were given by Flammer [38] in 1951, along with some numerical details.

Expressions for the coefficients in the series development of the eigenvalues in powers of c² up to and including the term in c⁸ were published by Bouwkamp [39] in 1950; they had been derived by him much earlier, however. Meixner [28] had already given numerical values for many of the coefficients of the terms in the power-series representations of the eigenvalues as well as of the expansion coefficients, up to and including the term in c¹⁰. The radii of convergence of the power-series developments were studied by Schmid [40] in 1948 and 1949. Bouwkamp [41] also discussed in 1950 various types of expansions for the functions of order zero. During the period 1948-51 Meixner [42, 99, 100] investigated various types of series developments of the spheroidal functions. The work of Meixner has been incorporated in the recently published book on Mathieu and spheroidal functions by Meixner and Schäfke [43], in which there has been presented a thorough analytical treatment of the spheroidal functions of unrestricted order.

A recent development in the theory of spheroidal functions has been the work of Marx [44, 45] on ‘recurrence’ relations for the spheroidal wave functions of the type introduced for Mathieu functions by Whittaker [46] in 1929. The coefficients in these relations are integrals of products of spheroidal functions. Additional integral relations involving products of spheroidal functions have been obtained by Chako [102]. Series developments of the products of two spheroidal functions in terms of products of spherical Bessel and associated Legendre functions were given earlier by Meixner [100].

Much of the aforementioned work has been compiled and extended in the present monograph.

1.2 Survey of Applications

Concomi...

Table of contents

• contents
• chapter 1. introduction
• chapter 2. separation of the scalar wave equation in spheroidal coordinates
• chapter 3. the angle functions
• chapter 4. the radial functions
• chapter 5. integral representations and relations
• chapter 6. expansions in spherical bessel function products
• chapter 7. recurrence relations of whittaker type
• chapter 8. asymptotic expansions for large values of
• chapter 9. vector wave functions
• appendix
• references
• tables of numerical values