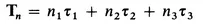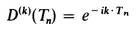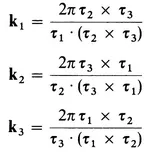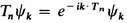Solid State Theory

Walter A. Harrison

• Publisher: Dover Publications
• Year: 2012
• ISBN:
  9780486152233
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

"A well-written text... should find a wide readership, especially among graduate students." — Dr. J. I. Pankove, RCA.
The field of solid state theory, including crystallography, semi-conductor physics, and various applications in chemistry and electrical engineering, is highly relevant to many areas of modern science and industry. Professor Harrison's well-known text offers an excellent one-year graduate course in this active and important area of research. While presenting a broad overview of the fundamental concepts and methods of solid state physics, including the basic quantum theory of solids, it surpasses more theoretical treatments in its practical coverage of physical applications. This feature makes the book especially useful to specialists in other fields who many encounter solid state problems in their own work. At least one year of quantum mechanics is required; however, the author introduces more advanced methods as needed.
Because virtually all of the properties of solids are determined by the valence electrons, the author devotes the first third of the book to electron states, including solid types and symmetry, band structure, electron dynamics, the self-consistent-field approximation, energy-band calculations, semi-conductor and semi-metal bands, impurity states, the electronic structure of liquids, and other topics. Dr. Harrison then turns to a more systematic treatment of the electronic properties of solids, focusing on thermodynamic properties, transport properties (including the Boltzmann equation), semi-conductor systems, screening, optical properties, the Landau theory of Fermi liquids, and amorphous semi-conductors.
In the final two chapters, Professor Harrison offers a cogent treatment of lattice vibrations and atomic properties and cooperative phenomena (magnetism and superconductivity). In addition to traditional background information, the book features penetrating discussions of such currently active problems as the Mott transition, the electronic structure of disordered systems, tunneling the Kondo effect, and fluctuation near critical points. In an important sense, the entire text constitutes a major vehicle for the clarification of quantum mechanics, resulting from, among other factors, a comparison of the semi-classical (Boltzmann equation) treatment of screening and the corresponding quantum (Liouville equation) treatment.

II

ELECTRON STATES

We have indicated in the preceding section how energy bands arise from the existence of the translation group in a one-dimensional crystal. We will first generalize that description to three dimensions and then look in some detail at the nature of the energy bands themselves.

1. The Structure off the Bands

We have defined for an arbitrary structure the primitive lattice translations τ₁, τ₂, and τ₃. The translation group of the crystal consists of sums of integral multiples of these three translations. For a general crystal structure these τ_i may be of different lengths and they need not be orthogonal. However, we have required that they not be coplanar.

We will again take periodic boundary conditions as we did in the one-dimensional case. We consider a system in the shape of a parallelepiped with edges N₁τ₁, N₂τ₂, and N₃τ₃, In a translation parallel to τ_1, for example, we envisage the atoms transferred out of the boundary as reentering on the opposite face so that the crystal within our boundaries remains invariant under the translation. In addition, the periodic boundary conditions require that the slope and value of any wavefunction be the same on opposite faces of the system. The translation group contains N₁N₂N₃ distinct translations, which may be written

(2.1)

with 0 ≤ n_i < N_i. In analogy with the one-dimensional case the irreducible representations are written

(2.2)

where k is now a vector and a dot product appears in the exponent. Each k corresponds to a different irreducible representation of the group. These k’s may be written as linear combinations of primitive lattice wavenumbers, k₁, k₂, and k₃.

(2.3)

where the k_i are integers and

(2.4)

Substituting Eq. (2.1) into Eq. (2.2) and writing out k we may readily verify that these representations have the same multiplication table as the translation group and are therefore representations of the group. We have distinct representations for N_i consecutive integers k_i. Thus there are as many irreducible representations given in Eq. (2.2) as there are symmetry operations in the translation group and this gives all of the irreducible representations of the translation group.

We again characterize each electron state by the wavenumber k corresponding to the irreducible representation according to which it transforms.

We again define Bloch functions u_k = e^–ik⋅rψ_k. In terms of these the wavefunction is

ψ_k = u_k e^ik⋅r

and u_k is seen to have the full translational symmetry of the lattice.

We may note that a representation corresponding to a wavenumber k is the same as a representation corresponding to

k ₊ m₁k₁ + m₂k₂ + m₃k₃

where the m_i are integers. The addition of these extra terms does not modify the value of any of the representations of Eq. (2.2). Thus we have an arbitrariness in the choice of k which is to be associated with any given representation. It is desirable to prescribe a unique choice and this is customarily done by selecting for any representation the shortest wavenumber that will generate it. (This is consistent with our selection in the case of one dimension.) The resulting domain of k is the three-dimensional Brillouin zone, and the wavenumbers in the Brillouin zone are frequently called reduced wavenumbers.

Note that the set of wavenumbers m₁k₁ + m₂k₂ + m₃k₃ forms a lattice in wavenumber space. We will call this the wavenumber lattice and refer to the points making up the wavenumber lattice as lattice wavenumbers. In diffraction theory it is more customary to discuss the reciprocal lattice which is the corresponding lattice in reciprocal space. The reciprocal lattice vectors are (2π)⁻¹ times the wavenumber lattice vectors. It is common terminology in solid state physics to call the wavenumber lattice the reciprocal lattice. However, in order to avoid the ambiguity with respect to the factor 2π, we will use the term wavenumber lattice. The symbols k₁, k₂, and k₃ are primitive lattice translations in the wavenumber lattice.

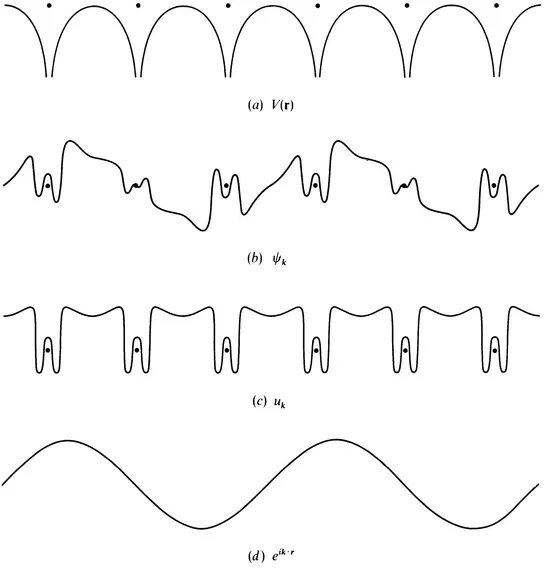
Before proceeding with the formal consequences of translational symmetry, it may be helpful to give a more pictorial description of the states and see the meaning of the multiple wavenumbers which could be associated with a given state. We are assuming a potential that has the full translational symmetry of the lattice. This is illustrated for a line through a series of atoms in Fig. 2.1a. Because of the periodicity this potential could be expanded in a Fourier series including only plane waves with wavenumber equal to a lattice wavenumber. (This follows in detail from the Fourier integral and will be demonstrated in Sec. 4.2 of this chapter.)

We have seen that the electronic eigenstates, illustrated in Fig. 2.1b, can be factored into a Bloch function, u_k, and a plane wave, e^ik⋅r, shown in Fig. 2.1c and 2.1d. The plane wave (as well as u_k) satisfies periodic boundary conditions. Because u_k has the full periodicity of the lattice, it could be expanded in a Fourier series including only lattice-wavenumber plane waves. It follows that the eigenstate can be expanded in a Fourier series containing plane waves of wavenumber k and wavenumbers differing from k by lattice wavenumbers; these are just the wavenumbers that generate the representation according to which ψ_k transforms.

Consequently, if we could precisely measure the true momentum of an electron in the state ψ_k, we could obtain a value corresponding to any one of these wavenumbers. The state ψ_k is not an eigenstate of true momentum since by moving in a potential field the electron is continuously exchanging momentum with the lattice, but because of the periodicity it does not contain components of all momentum values, just those corresponding to the wavenumbers which generate the appropriate representation. Such a description is one way of giving physical content to the ambiguity in the wavenumber to be associated with a state.

Fig. 2.1 A schematic representation of electronic eigenstates in a crystal. (a) The potential plotted along a row of atoms. (b) A sample eigenstate; the state itself is complex but only the real part is shown. This state can be factored into Bloch function (c), which has the periodicity of the lattice, and (d) a plane wave, the real part of which is shown.

We have found that a given wavenumber k ...

Table of contents

• Title Page
• Copyright Page
• Dedication
• PREFACE
• Table of Contents
• I - SOLID TYPES AND SYMMETRY
• II - ELECTRON STATES
• III - ELECTRONIC PROPERTIES
• IV - LATTICE VIBRATIONS AND ATOMIC PROPERTIES
• V - COOPERATIVE PHENOMENA
• INDEX