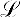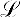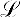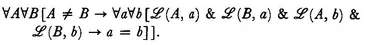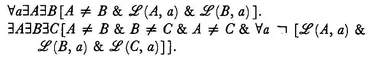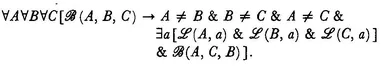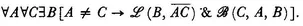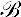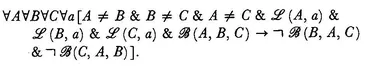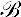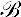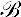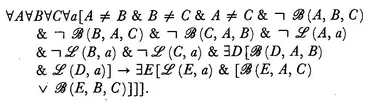Philosophy of Mathematics and Deductive Structure in Euclid's Elements

Ian Mueller

• Publisher: Dover Publications
• Year: 2013
• ISBN:
  9780486150871
• Topic: Mathematics
• Subtopic: History & Philosophy of Mathematics
• Index: Mathematics

A survey of Euclid's Elements, this text provides an understanding of the classical Greek conception of mathematics. It offers a well-rounded perspective, examining similarities to modern views as well as differences. Rather than focusing strictly on historical and mathematical issues, the book examines philosophical, foundational, and logical questions.
Although comprehensive in its treatment, this study represents a less cumbersome, more streamlined approach than the classic three-volume reference by Sir Thomas L. Heath (also available from Dover Publications). To make reading easier and to facilitate access to individual analyses and discussions, the author has included helpful appendixes. These list special symbols and additional propositions, along with all of the assumptions and propositions of the Elements and notations of their discussion within this volume.

1

Plane Rectilineal Geometry

1.1 Hilbert’s Geometry and Its Interpretation

Of all the differences between Greek and modern mathematics, the most fundamental concerns the role of geometry in each. One might say that the history of nineteenth-century mathematics is the history of the replacement of geometry by algebra and analysis. There is no geometric truth which does not have a nongeometric representation, a representation which is usually much more compact and useful. Indeed, many mathematicians might prefer to say that traditional or descriptive geometry is simply an interpretation of certain parts of modern algebra. For such people geometry is of no real “mathematical” interest.¹ The marginal position of geometry in modern mathematics is a complete contrast to its central position in the Elements and other classical Greek mathematical texts. One could almost say that Greek mathematics is nothing but a variety of forms of geometry. The extent to which this assertion is true is one interpretative crux to which this book is addressed. However, the most elementary part of Euclid’s geometry will be my first concern here. And although it would be possible and enlightening to contrast this with algebraic treatments of corresponding subjects, it is more useful to consider modern treatments of elementary Euclidean geometry which do not invoke algebra in an essential way. The outstanding and most influential work in this relatively narrow field is undoubtedly Hilbert’s Grundlagen der Geometrie, first published in 1899. I shall simply quote from and paraphrase the beginning of this work.

1. The elements of geometry and the five groups of axioms. Explanation. We consider three distinct systems of objects: we call the objects in the first system points and designate them by A, B; C, . . . ; we call the objects of the second system straight lines and designate them by a, b, c, . . . ; we call the objects of the third system planes and designate them by α, β, γ, . . . .

We consider these points, straight lines, and planes to be in certain relations to one another and designate these relations by words like ‘lie’, ‘between’, ‘congruent’, ‘parallel’, ‘continous’ ; the exact and, for mathematical purposes, complete description of these relations is accomplished by the axioms of geometry.

Hilbert goes on to describe the five groups of axioms, each of. which “expresses certain associated fundamental facts of our intuition.” He then gives the axioms of the first group, the axioms connecting points, lines, and planes together. I give here the first three of these axioms and the axioms of group II, the axioms of order, in English and then in logical notation.²

I,1 For any two points A, B, there is always a straight line a associated with both of the two points A, B.

∀B [A B → ∃a [

(A, a) &

(B, a)]].

(

(, a) should be read as ‘A lies on a’.)

I,2 For any two points A, B, there is not more than one straight line associated with both of the two points A, B.

I,3 On a straight line there are always at least two points. There are at least three points which do not lie on one straight line.

II,1 If a point A is between a point B and a point C, then A, B, C are three distinct points on a straight line and A is between C and B.

(

(A, B, C) is read as ‘A is between B and C’.)

II,2 Given two points A and C there is always at least one point B on the straight line AC such that C is between A and B.

The straight line AC is defined to be the straight line the existence and uniqueness of which follow for given distinct points A and C from axioms I,1 and I,2. In the logical formulation of the axiom the phrase ‘the straight line AC′ is represented by

:

An essential feature of a defined term is that its use can be avoided in favor of the terms in its definition. Axiom II,2 could be stated

Given two points A and C there is always at least one point B and a straight line a such that A, B, C lie on a and C is between A and B.

In fact because of II,1 it would be sufficient to write

II,2′ Given two points A and C there is always at least one point B such that C is between B and A.

∀A∀C[A ≠ C → ∃B

(C, B, A)].

The third axiom of the group is

II,3 For any three points on a line, not more than one of them is between the other two.

Because of II,1 I will be able to use the simpler formulation

∀A∀B∀C [

(A, B, C) → ¬

(B, A, C) & ¬

(C, A, B)].

After stating this axiom Hilbert gives the following explanation:

We consider two points A and B on a straight line a. We call the system of both points A and B a segment and designate this by AB or BA. The points between A and B are called points of the segment AB or points lying within the segment AB . . . .

He then gives the next axiom.

II,4 Let A, B, C be three points not lying on a straight line and a a straight line . . .³ which meets none of the points A, B, C: if the straight line a goes through a point of the segment AB then it certainly also goes either through a point of the segment AC or through a point of the segment BC.

There are difficulties involved in rendering this axiom in logical notation. Hilbert apparently thinks of the notion of a system as a logical notion like our notion of a pair or couple. It would be possible to follow him here, but it seems simpler to avoid the notion of segment altogether. The following symbolization of II,4 accomplishes this purpose:

Here is the first proof in the Grundlagen:

Figure 1.1

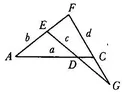
Theorem 3. Given two points A and C there is always at least one point D on the straight line AC which lies between A and C.

Proof: According to axiom I,3 there is a point E outside the straight line AC [fig. 1.1] and according to axiom II,2 there is a point F on AE such that E is a point of the segment AF. According to the same axiom and according to axiom II,3 there is a point G on FC which does not lie on the segment FC. According to axiom II,4 the straight line EG must then intersect the segment AC in a point D.

It would be possible to represent this proof written in English prose as a finite sequence of logical formulas each of which is either an axiom or a syntactic transformation of previous formulas in the sequence in accordance with fixed rules. If the rules were standard ones, such a representation would require more than 100 such formulas and would be virtually unintelligible unless read in the light of Hilbert’s proof. However, the possibility of such a representation has an effect on the philosophical interpretation of Hilbert’s geometry, to which I now turn.

Hilbert’s Grundlagen is open to several such interpretations, all compatible with his prose explanations. One is based on his characterization of the axioms as expressions of fundamental...

Table of contents

• DOVER BOOKS ON MATHEMATICS
• Title Page
• Copyright Page
• Table of Contents
• Acknowledgments
• Introduction
• Bibliographical Note
• 1 - Plane Rectilineal Geometry
• 2 - Euclidean Arithmetic
• 3 - Magnitudes in Proportion
• 4 - Proportion and the Geometry of Plane Rectilineal Figures
• 5 - The Circle and Its Relation to the Triangle, the Square, and the Regular Pentagon, Hexagon, and Pentekaidekagon
• 6 - Elementary Solid Geometry and O the Method of Exhaustion
• 7 - The Investigation of the Platonic Solids
• Appendix 1 Symbols and Abbreviations
• Appendix 2 Euclidean an Assumptions
• Appendix 3 Additional Propositions
• Appendix 4 The Contents of the Elements
• Bibliography
• Index