Matrices and Graphs Stability Problems in Mathematical Ecology

D. Logofet

• Publisher: CRC Press
• Year: 2018
• ISBN:
  9781351091220
• Edition: 1
• Topic: Biological Sciences
• Subtopic: Ecology
• Index: Biological Sciences

Intuitive ideas of stability in dynamics of a biological population, community, or ecosystem can be formalized in the framework of corresponding mathematical models. These are often represented by systems of ordinary differential equations or difference equations. Matrices and Graphs covers achievements in the field using concepts from matrix theory and graph theory. The book effectively surveys applications of mathematical results pertinent to issues of theoretical and applied ecology.
The only mathematical prerequisite for using Matrices and Graphs is a working knowledge of linear algebra and matrices. The book is ideal for biomathematicians, ecologists, and applied mathematicians doing research on dynamic behavior of model populations and communities consisting of multi-component systems. It will also be valuable as a text for a graduate-level topics course in applied math or mathematical ecology.

CHAPTER 1

Stability Concepts In Ecology and Mathematics

Understood generally as an ability of a living system to persist in spite of perturbations, stability can be defined in many ways, both in verbally descriptive and formal terms, either in ecology or mathematics. While neither one of these “ecological” meanings of stability can now be recognized as being more fundamental than the other, mathematics has the greater advantage, since it has given rise to the notion of Lyapunov stability, which appears to be inherent in or important to any further conceptions of stability—at least, within the theory of dynamical systems. To see whether and how this mathematical substantiality has produced any consequences in ecology, we concentrate, in this introductory chapter, on the way this notion is applied in mathematical theory of population, community, or ecosystem dynamics, or more shortly, in the proper chapters of mathematical ecology.

I. Basic Approaches to the Notion of Stability

In spite of appearing to be intuitively clear, “an ability to persist in spite of perturbations” can scarcely be defined in a unique and unambiguous way. The reason for this difficulty is that both the “persistence” and the “perturbations” parts of the idea need further clarification, to say nothing of the scale factors of the system being considered. What is understood by “an ability to persist” and what kind of “perturbations” is relevant? Different answers to these basic questions and a variety of stability concepts have been proposed and discussed in the ecological literature,^{1 and 2} (yet only a few of them have been given proper mathematical attention^{3 and 4}). Perhaps this is why stability in general lacks—and should apparently not have—any “stable” definition.

A. Species Diversity as a Measure of Stability

It has long been a paradigm of theoretical ecology that the more complex the structure of a biological community is and the more abundant the number of constituent species in it, the more stable the community will be in response to perturbations.^{5 and 6} The argument in favor of this thesis—first proposed apparently by MacArfhur⁷ and Elton⁸—is briefly as follows. Various species have different ranges of adaptation to changes in their environment. A wider species composition may therefore respond to various environmental changes more successfully than a community with a lower number of species. The former is hence considered to be more stable than the latter. This is probably the main reason why a variety of species diversity indices (in particular, the entropy of information theory or its analogs) are used to characterize the community’s stability.⁶

The most popular index is the Shannon information entropy measure:

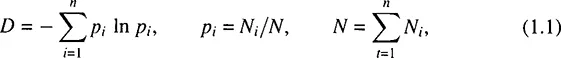
where n is the number of species in a community, N_i is the population size of the ith species. A somewhat different measure, but of the same genus, is the index

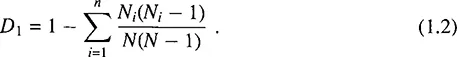
It can be shown that D₁ represents the probability that two individuals, when chosen randomly from a set of N ones, do not belong to the same species. For large values of N and uniform enough distribution of N among species, the proportion of species i can be assumed to approximate p_i ≈ 1 + In p_i, whereby it can be shown that D₁ ≈ D.

Other definitions of this kind (e.g., those using R. A. Fisher’s measure of information) have also been proposed as stability measures, yet all of them rely upon notions originating from theoretical physics or information theory (see a survey by Goodman⁶). There is no doubt that diversity measures do carry some objective information about the properties of a system. E. Odum⁹ has shown, for instance, that there are certain relationships among the diversity level, the structure, and the functioning of energy flows in an ecosystem. However, using such diversity indices as stability measures leads to some drawbacks, or paradoxes, in the theory,^10,4 where a typical “route” to a drawback can be traced in the following argument.

Under the “maximum diversity-maximum stability” assumption, it would be logical to suppose further that maximum stability is attained at equilibrium, if this state is ever reached. A simple exercise in finding a conditional maximum of a function like D(p) over the space of frequencies p_i will then readily generate a fixed pattern of equilibrium distribution, which can hardly be interpreted in ecological terms. For example, the maximum of D (1.1) is attained at p* = [1/n, 1/n,..., 1/n], i.e., at uniform species abundance. This excludes any species domination or quantitative hierarchy in the community, whereas the empirical evidence is just the opposite: communities which exist long enough to be considered stable do feature dominating species, which carry out the major part of the work to provide for the matter and energy turnover through the ecosystem.¹¹ In other words, a quantitative hierarchy, rather than uniformity, is normal for a real system.

Other diversity indices may, of course, generate hierarchical distributions too, but the causes of the hierarchy will always be fixed to a particular mathematical form of the diversity function to be maximized, rather than to real properties of the system under study. That is why the use of diversity indices as measures of stability can scarcely be accepted as a faultless approach.

On the other hand, an increase in diversity may really be observed in many natural and laboratory communities, particularly at the early stages of their evolution to an equilibrium state. To all appearances, the diversity measures are still able to characterize a community in some dynamic respects, although falling short of general applicability.

The reason for such paradoxes probably arise because the models of theoretical physics and information theory are formally applied to systems to which they are not applicable. Both the Boltzmann entropy in statistical physics and the information entropy in information theory make sense only for ensembles of weak interactions among particles or other objects. Introducing an entropy measure is grounded quite well for such ensembles. But once we turn to systems whose elements interact strongly, the entropy measure can no longer suffice. Biological communities and ecosystems represent systems with strong interactions, because it is mainly the interactions themselves among constituent species or ecosystem components that form the structure of the system.

As far as a steady equilibrium can be regarded as the final outcome of the functioning of structure, quite explainable may be progress in the application of entropy measures at early stages of community evolution. The point is that, these stages being far from equilibrium, the competition or other interactions among species are still we...

Table of contents

• Cover
• Title Page
• Copyright Page
• Preface
• Acknowledgments
• Dedication
• Table of Contents
• 1 Stability Concepts In Ecology and Mathematics
• 2 Leslie Matrix Model
• 3 Modifications of the Leslie Model
• 4 Lotka-Volterra Models of n-Species Communities
• 5 Stability Analysis on Community Graphs
• 6 Trophic Chains and Stability in Vertical-Structured Communities
• 7 Ecological Niche Overlap and Stability in Horizontal-Structured Communities
• 8 Stability in “Box” Models of Spatial Distribution
• Epilogue
• List of Notation
• Index