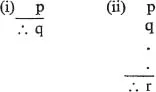The Elements of Formal Logic

G. E. Hughes, D. G. Londey

• Publisher: Routledge
• Year: 2019
• ISBN:
  9781000737042
• Edition: 1
• Topic: Filosofia
• Subtopic: Storia e teoria della filosofia

Originally published in 1965. This is a textbook of modern deductive logic, designed for beginners but leading further into the heart of the subject than most other books of the kind.

The fields covered are the Propositional Calculus, the more elementary parts of the Predicate Calculus, and Syllogistic Logic treated from a modern point of view. In each of the systems discussed the main emphases are on Decision Procedures and Axiomatisation, and the material is presented with as much formal rigour as is compatible with clarity of exposition. The techniques used are not only described but given a theoretical justification. Proofs of Consistency, Completeness and Independence are set out in detail. The fundamental characteristics of the various systems studies, and their relations to each other are established by meta-logical proofs, which are used freely in all sections of the book. Exercises are appended to most of the chapters, and answers are provided.

CHAPTER 1

Validity

Everyone knows that Formal Logic has something to do with argument or reasoning. Some think that it is a sophistic art, an art of winning arguments; others, nearer the mark, think that it is the more reputable sophistic art of reasoning correctly and spotting fallacious arguments when others use them; others, still nearer the mark, think of it less as an art or technique and more as an intellectual study of the structures of arguments or inferences, classifying them as sound or fallacious. We can get a good deal nearer the mark still by saying that Formal Logic is the study of the structures of propositions and deductive inferences. This remark is not offered as a definition of ‘formal logic’, but rather as an indication of the sort of subjects discussed in this book. Indeed it is not clear that any adequate definition of ‘formal logic’ (let alone ‘logic’) is possible – if you want to know what Logic is about, then you must set to work and do some. Let us get down to it.

Our subject revolves round the notion of validity, and the main purpose of this chapter is to give some explanation of this notion. But before we can address ourselves directly to this task, we need to introduce a few other terms. Since we shall be thus steadily building up a precise technical language you should make quite sure that you have understood and learned the explanation of each new term as it appears.

Propositions and propositional schemata

A proposition is a statement. It is either true or false. The following are propositions:

Today is Tuesday
7 is a prime number
If he goes to town, he will buy some sugar
Socrates was not the brother of Plato.

A propositional form or schema (plural: schemata) is an expression containing blanks, such that if these blanks are filled in an appropriate way, the result is a proposition. Thus:

All ——— are …

is a propositional schema. However, for reasons of convenience, we shall use letters instead of dots and dashes to mark the blanks. Such letters are known as variables. The following are propositional schemata:

(i) All S are P

(ii) n is a prime number

(iii) If n is a prime number greater than 2, then n is odd

(iv) If p, then q.

In order to get a proposition from a propositional schema we must fill in the blanks appropriately, or, as we say, make appropriate substitutions for the variables. Thus, in (ii) it is no use replacing ‘n’ by a proposition – only a number will do. And the same holds for (iii). Similarly we can get a proposition from (iv) only by replacing ‘p’ and ‘q’ by propositions. So we say that ‘n’ in (ii) and (iii) is a numerical variable, and that ‘p’ and ‘q’ in (iv) are propositional variables. A numerical variable like ‘n’ is said to take numbers as values, while a propositional variable like ‘p’ is said to take propositions as values.

We shall reserve the letters ‘p’, ‘q’, ‘r’, ‘s’, ‘t’,… for propositional variables. Where no ambiguity will result we shall occasionally use the word ‘proposition’ to mean ‘propositional schema’.

Inferences and inferential schemata

An inference is the passage from the assertion of one proposition (the premiss) or group of propositions (premisses) to the assertion of another proposition (the conclusion). The following are inferences:

(i) All kangaroos eat grass, therefore some kangaroos eat grass.

(ii) Every kangaroo I have observed eats grass, therefore some kangaroos eat grass.

(iii) Every kangaroo I have observed eats grass, therefore kangaroos generally eat grass.

(iv) Every kangaroo I have observed eats grass, therefore all kangaroos eat grass.

(v) Some kangaroos eat grass, therefore all kangaroos eat grass.

(vi) Some kangaroos eat grass, therefore there is a man on the moon.

(vii) Kangaroos have such and such a sort of teeth, therefore they probably eat grass.

(viii) All kangaroos are marsupials and some grass-eaters are kangaroos; but Charlie is a grass-eater – so Charlie must be a marsupial.

Inferences are commonly classified into deductive and inductive inferences. Either sort may be sound or unsound. Of the examples given, (i), (ii), (v) and (viii) would usually be regarded as deductive inferences, the rest as inductive. (Go through these examples deciding which are sound and which are unsound inferences, and why. In the light of your conclusions, try to formulate some basis for the deductive/inductive classification.) In this book we shall be concerned only with various forms of deductive inference, and as you work through it your insight into the nature of this type of inference will grow.

It is perhaps going a little beyond ordinary usage to say that (vi) is an inference at all, since we tend to demand some connection of content between the premisses and the conclusion before we are willing to use the word ‘inference’. But it is extremely difficult to make this demand precise; and even if we were to succeed in doing so we would be likely to succeed too well, limiting the meaning of ‘inference’ to that of ‘sound inference’ – and we know only too well that there is such a thing as an unsound inference! It is for this reason that we have adopted a very general account of the nature of an inference, even though this means that we must accept as inferences such queer fish as (vi).

A form of inference or inferential schema is an expression containing blanks, such that if these blanks are filled appropriately the result is an inference. Or, alternatively, it is an expression containing variables, such that if appropriate substitutions are made for the variables, the result is an inference.

The most general forms of inference are:

(i) p, therefore q (single premiss)

(ii) (p, q, …), therefore r (more than one premiss)

Convenient alternative ways of writing these schemata are:

There are of course infinitely many specialized forms of these most general forms. For example,

is a special case of (i).

We are now in a position to begin on our main task of explaining validity, and we begin by introducing the notion of a valid deductive inference. An inference is a valid deductive inference if and only if the conclusion logically follows from the premiss(es); that is, if and only if the truth of the prrmiss(es) gives an absolute guarantee of the truth of the conclusion. It can be seen that a valid inference is a sound inference, and that the heart of this notion of validity is that the combination of true premisses and false conclusion is ruled out.

An inferential schema is, as it were, a pattern for a set of inferences, and we extend the notion of validity to cover such a schema by requiring that every inference constructed on that pattern should be valid. To state it more precisely, an inferential schema is valid if and only if every set of appropriate and uniform substitutions for all its variables yields a valid inference. The substitutions must be appropriate in the sense described earlier – i.e. we must substitute the type of expression appropriate to the variable – and they must also be uniform in the sense that, if a variable appears twice in a given schema, we must make the same substitution for it in each case. Consider the schema

(p, q), therefore q.

For the substitutions to be uniform we must put the same proposition for ‘q’ in the conclusion as in the premiss. But of course we may substitute a different proposition for ‘p’ from the one we substitute for ‘q’, although it is not necessary to do so.

Classification of propositions

A proposition may be either necessarily true, contingent or necessarily false. Every proposition is of one of these kinds.

A proposition is necessarily true if there is no conceivable circumstance in which it would be false – or, as Leibniz¹ put it, if it is true in all possible worlds.

A proposition which is not necessarily true may be either contingent (true or false, but not necessarily so) or necessarily false (‘impossible’). Thus:

¹ G. W. Leibniz (1646–1716) – a famous German philosopher, logician, mathematician, natural scientist and diplomat.

(i) A brown cow is a cow

(ii) If all triangles are equilateral, then some triangles are equilateral

are necessarily true.

(iii) England is a monarchy

is contingent – it happens to be true, but we could imagine circumstances in which it would be false.

(iv) France is a monarchy

is contingent – it happens to be false.

(v) All round objects are square

is necessarily false – we could imagine no set of circumstances in which it would be true.

Classification of propositional schemata

The classification of propositional schemata is analogous to that of propositions. A propositional schema may be either valid, contingent or inconsistent. Every propositional schema is of one of these kinds.

A propositional schema is valid if and only if eve...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Original Half Title
• Original Title Page
• Original Copyright Page
• Contents
• Preface
• Some Suggestions on the Use of this Book
• Chapter 1 Validity
• Part I: The Propositional Calculus: Elements and Decision Procedures
• Part II: The Propositional Calculus: Axiomatic Systems
• Part III: The Lower Predicate Calculus
• Part IV: Syllogistic
• Appendices
• Answers to Exercises
• Some Suggestions for Further Reading
• Index
• Abbreviations and Special Symbols