Understanding Buildings a Multidisciplinary Approach

E. Reid

• Publisher: Routledge
• Year: 2013
• ISBN:
  9781317901907
• Edition: 1
• Topic: Tecnologia e ingegneria
• Subtopic: Ingegneria edile

This book meets the needs for a basic, yet comprehensive and up-to-date, introductory text to building technology for students in architecture and the other disciplines in building design.The wide coverage is organised under the chapter headings: structure, enclosure, climate services, utility services, lighting, acoustics, fire safety, the future? The treatment in each case is concentrated on the close relationship between good design practice and the basic underlying scientific and practical principles, but stopping short of the high level theory which is to be found in other more closely specialised texts.This well illustrated and highly readable book will be invaluable to the student and of interest to the practitioner too, both in architecture and in its related technical fields.

1

STRUCTURE

INTRODUCTION

The first thing that any building has to do is stand up. The building is hardly there to satisfy the needs of structure but, whatever its purpose and plan, structural needs will have had a vital hand in shaping its form. And yet, we are so used to buildings not falling down that we hardly stop to wonder why they do not. In fact, ‘structure’ is often thought of as a rather rarefied subject obscured by tedious sums, but it need not be so, for sums do not in themselves shape structural design and nor are they essential to a basic understanding of the principles from which structural solutions spring.

Why does, say, a simple stone tower stand? With no special knowledge, we can say ‘because the walls are vertical and thick and because the floors and roof have strong enough beams to span’. True, this may not take us far in comprehending the structure of cathedrals and high-rise buildings, but it is a start. Our everyday experience brings us an intuitive grasp of structure, a feeling for what is structurally right. We have all experienced how materials behave. Observation has told us that stone and wood are relatively strong and bananas and blotting paper weak, and we expect tree branches to thicken towards the trunk and need no sums to tell if a fence is strong enough to sit on.

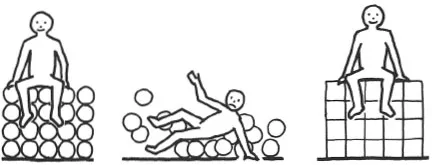
Certainly, our intuition is fallible. At the risk of irritating readers more familiar with structures, which of the spans in 1.1 is the stronger? Be assured, you are in numerous company if you pick the left one at first glance, where the struts and wires are doing nothing useful at all. But then, again, it only takes a moment’s extra thought to understand the arrangement and set the matter right – thought, that is, coupled with quite ordinary experience?

1.1 Which of the two spans is the stronger?

This kind of intuition, and experience, often from hard trial and error, must have schooled the early builders. They did no sums in the modern way but their skilled traditions grew. The mediaeval master masons were delicately balancing the outward thrust of cathedral arches with the counter-thrust of external buttresses, long before the beginnings of modern theory when men like Galileo in the seventeenth century came to wonder about the mathematics of bending, and Newton about the action and reaction of forces, and Hooke about how materials deform under load.

Where, then, does calculation come in? Well, for one thing stress calculations enable engineers to check whether their assumptions about the likely behaviour of their structural proposal are correct. The intuitive, or empirical, can be mathematically verified. In this respect, the early builders were blindfold and, despite their achievements, they sometimes did get it wrong – in quantity, if not in concept. On Beauvais cathedral the roof fell twice and the tower once. Winchester collapsed. Wells, propped too much by the stone buttresses outside, had to be counter-propped by buttresses inside. Many mishaps were due to men who were uncertain of the stresses their structure had to take and dared too much. They could only follow what modern jargon has called the PPI rule – the ‘put plenty in’ rule – making elements more massive and hoping to err on the safe side: at least they had ample labour force and ample stone. In the advancing iron technology late last century, it took a whole series of collapses – about 25 bridges a year in America – before it was finally accepted that, as structures got larger, commonsense rules-of-thumb simply had to be backed up by calculations.

More specifically, there is the need to minimise self-weight. Just ‘putting plenty in’ is hopeless in terms of structural economy. Having the structural parts bigger than they need to be wastes material and demands that the structure be even bigger, to carry its own superfluous weight – a vicious circle that is ever more critical as scale increases. For instance, if you spanned a wooden metre rule across a gap it would be stiff and could carry a load much greater than its own weight. But if you increased all the dimensions a hundredfold, creating a plank spanning 100 m, the plank would sag and break under its weight alone. This is called scale effect. Suppose a 1 cm cube is increased in size to a 2 cm cube, and then to a 3 cm cube. The area of a cross-sectional slice goes up in the ratio 1 : 4 : 9, but the volume goes up in the ratio 1 : 8 : 27. Volume increases faster than cross-section, so to speak. As we increase the plank size, the volume and, hence, weight, soon outstrip the ability of the cross-sectional area, i.e. the plank’s ‘thickness’, to cope. Weight overtakes strength. In nature, it is the reason why spiders have thin legs and elephants have fat ones. In building structure, it is the reason why a room can be economically spanned by a wooden joist, while the factory roof-span needs, say, an open-web truss, and a long river span, the ultimate efficiency of a lightweight suspension bridge.

But stress calculations do not define the shape of structure, they simply allow an exactness of sizing so that available strength is tailored to the loads with maximum economy, always allowing a known margin of safety. Exactness checks and trims the idea, it gets it right the first time, but we do not need the same exactness to understand the idea. The vaulted roofs of Sydney Opera House needed computers to solve the structural problems they posed and yet their final shape reflects the first idea of an architect watching the sails of yachts in a bay.

THE ARCHITECTURE OF COMPRESSION

As soon as man learnt to pile up stones for shelter, he started to play the compression game. Stone is strong under compression but pulls apart fairly easily under tension and, moreover, stones in a wall lock together under compression but under tension can pull apart at the joints. The need to keep stones or bricks, or other blocks, under compression has influenced the shape of every masonry building ever built.

HOW MATERIALS RESIST LOAD – THE WALL

Think of just one stone at the base of a wall. It must carry its share of the weight of the stones above – the wall’s deadload – and so must ‘press up’ as much as that weight is pressing down. If it pressed too little, the wall would squash, if it pressed too much, the stones above would presumably fly away. But it presses just the right amount and the system is stable. And, if someone sits on the wall, a minute part of their added liveload must reach the stone and the stone obliges by pushing up that fraction more. The system is still stable. But how does the stone and, for that matter, the earth below it, always know how much to push up? The answer to this apparently silly question has only been known for the past few decades, in fact: it lies at the microscopic scale of the atom and sheds light on the whole nature of structural strength.

The molecular ‘grid’

The component molecules of every substance are connected by forces which, for our purposes, can be regarded as magnetic springs. The rather notional three-dimensional grid (1.2) gives the general idea. It is these springs which compress or extend when a material is squeezed or stretched – a tiny deformation often, but it is there, for nothing is ever truly rigid. Even a marble slab is like a very stiff internally-sprung mattress and will compress locally as an ant walks over it, as will the ant’s feet. The world is a springy place. So, in fact, structure – materials – do not actively ‘push back’, but they deflect and, in doing so, find their passive reaction to loads placed upon them. You can see the deflection of a tree branch when you swing on it, and the flapping of an aircraft’s wings when it hits air turbulence, and you can just about feel the sway in some tall steel-frame buildings when the wind blows strongly. Wood and steel are relatively elastic. You will not notice the sag in a stone-arch bridge when a car crosses it, nor the compression in the wall stone, but they are there.

1.2 All matter is ‘springy’

Stiffness and strength

However, just because one material gives more, i.e. is more elastic than another, it is not necessarily weaker. A brittle dry twig will snap under load long before a green springy one, although the green one may, at first, have seemed the weaker. So stiffness is not the same as strength, although both qualities are needed in the materials we use for building. We will come back to this distinction later, particularly when talking of beams and frames.

Stress and strain

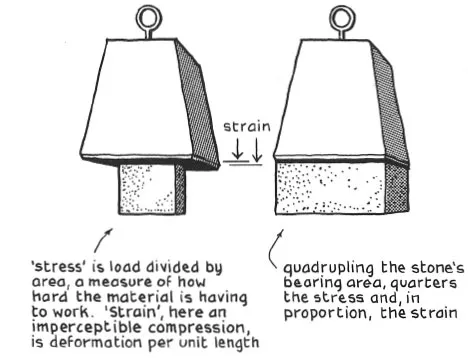
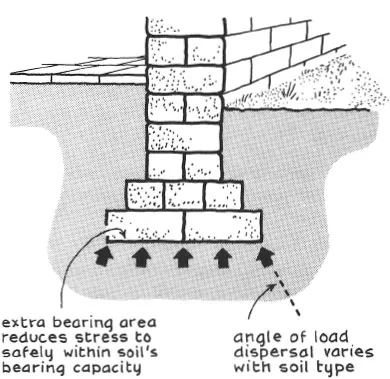
If the load on a stone is two tonnes, the stone must react with two tonnes’ force, but without knowing the bearing area of the stone, we cannot tell how hard the material is having to work (1.3). Instead, we must think in terms of stress. If the stone’s bearing area, is 1000 square centimetres (cm²), then the compressive stress in the material is 2 tonnes (or 2000 kilograms) force per 1000 cm² – i.e. 2 kgf/cm². The units do not matter. The same information could be given in pounds force per square inch or dynes per square centimetre, for stress is simply a ratio of load to bearing area – much more useful. Strain is the linear distortion in response to stress. Nails are pointed so that the impact load of the hammer is concentrated on a tiny area of the material pierced – maximum stress and strain to yield point, for minimum load. Obviously, the same load that produces a high stress in a thin wall will produce a safer, lower stress in a thick one. Foundations are made wider than walls to reduce compressive stresses to a level that weaker subsoils can bear. In contrast to the nail, the foundation (1.4) spreads the load, preventing the wall from punching through the ground, which would cause settlement and eventual building collapse.

1.3 Load and bearing area, stress and strain

1.4 Foundation, i.e. increased bearing, reduces soil stress

Shear

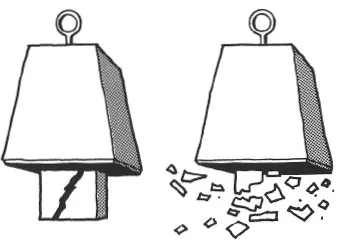
It may, at first, be hard to see how compressive stress could ever crush stone, instead of just compressing the atoms more tightly together. In fact, what happens at the point of failure is that the stone squashes out sideways, rather as clay will under the weight of a modeller’s hand, except that stone, being more brittle than clay, fails by cracking or even a virtually explosive release (1.5). The compressed material is actually failing by tensions induced within it. There is a slipping of adjacent molecular layers, and this we call shear.

1.5 Compression induces inner tensions and eventual failure by shear

1.6 Masonry is more stable and strong if well fitted …

On a larger scale, a wall can fail at the joints if the stones roll off one another (1.6), sliding into a heap, as a pile of cannon balls would. This is an extreme way of illustrating that a wall made of irregular boulders is weaker than one built with accurately cut rectangular blocks – the strength of early cathedrals owes much to the workmanship of long-forgotten masons.

Bonding

A masonry wall is also stronger if the horizontal courses of stones or bricks are staggered, so that the vertical joints are not continuous (1.7). If they were continuous, the wall would act like a series of adjacent, vertical piers, rather than as a cohesive unit. The interlocking bond has the further merit of dispersing point loads evenly.

1.7 … and more stable and strong still with an interlocking bond

THE NEED FOR STABILITY

But readers more familiar with structures may be getting worried by this focus on direct, compressive stress, knowing that masonry walls are usually too strong to fail by compression alone. In truth, the real danger is instability, overturning and buckling, and the higher and thinner the wall, the greater the danger becomes.

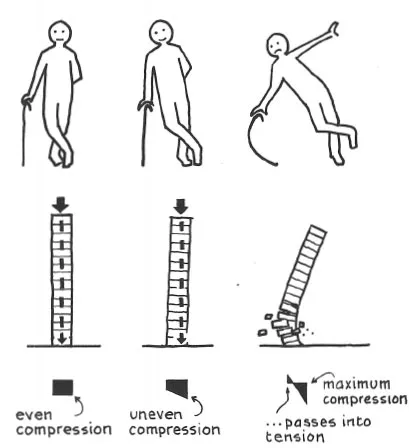
Suppose you lean on a flexible cane (1.8). As long as the cane remains absolutely straight, it can support you but, as soon as the slightest bending occurs, things become suddenly worse and over you go. If only you could be sure of keeping the direction line of your weight acting exactly through the centre of the cane down to the ground, you would be all right but, invariably, some slight twist of your hand on the handle, or some irregularity in the cane, will get the buckle started. We call this situation dynamically unstable.

1.8 Instability owing to buckling

So, either the wall can get out of line with its load or the load can get out of line with the wall. Take the first case. A vertically loaded wall is all nicely in compression – the stress distribution is ...