Structural Mechanics

A unified approach

Alberto Carpinteri

• Publisher: CRC Press
• Year: 2017
• ISBN:
  9781351990899
• Edition: 1
• Topic: Technik & Maschinenbau
• Subtopic: Bauingenieurwesen

This book presents a complete and unified treatment of the fundamental themes of structural mechanics, ranging from the traditional to the most advanced topics, covering mechanics of linear elastic solids, theory of beam systems, and phenomena of structural failure. The book considers explicitly all the static and kenetic operators of structural mechanics with their dual character.
Topics relating to structural symmetry are covered in a single chapter while dynamics is dealt with at various points. The logical presentation allows the clear introduction of topics such as finite element methods, automatic calculation of framed beam systems, plate and shell theory, theory of plasticity, and fracture mechanics.
Numerous worked examples, exercises with complete solutions and illustrations make it accessible both as a text for students and as a reference for research workers and practicing engineers.

1
Introduction

1.1 Preliminary remarks

Structural Mechanics is the science that studies the structural response of solid bodies subjected to external loading. The structural response takes the form of strains and internal stresses.

The variation of shape generally involves relative and absolute displacements of the points of the body. The simplest case that can be envisaged is that of a string, one end of which is held firm while a tensile load is applied to the opposite end. The percentage lengthening or stretching of the string naturally implies a displacement, albeit small, of the end where the force is exerted. Likewise, a membrane, stretched by a system of balanced forces, will dilate in two dimensions and its points will undergo relative and absolute displacements. Also three-dimensional bodies, when subjected to stress by a system of balanced forces, undergo, point by point and direction by direction, a dilation or a contraction, as well as an angular distortion. Similarly, beams and horizontal plates bend, imposing a certain curvature, respectively to their axes and to their middle planes, and differentiated deflections to their points.

As regards internal stresses, these can be considered as exchanged between the single (even infinitesimal) parts which make up the body. In the case of the string, the tension is transmitted continuously from the end on which the force is applied right up to the point of constraint. Each elementary segment is thus subject to two equal and opposite forces exerted by the contiguous segments. Likewise, each elementary part of a membrane will be subject to four mutually perpendicular forces, two equal and opposite pairs. In three-dimensional bodies, each elementary part is subject to normal and tangential forces. The former generate dilations and contractions, whilst the latter produce angular distortions. Finally, each element of beam or plate that is bent is subject to self-balanced pairs of moments.

In addition to the shape and properties of the body, it is the external loading applied and the constraints imposed that determine the structural response. The constraints react to the external loads, exerting on the body additional loads called constraint reactions. These reactions are a priori unknown. In the case where the constraints are not redundant from the kinematic point of view, the calculation of the constraint reactions can be made considering the body as being perfectly rigid and applying only the cardinal equations of statics. In the alternative case where the constraints are redundant, the calculation of the constraint reactions requires, in addition to equations of equilibrium, the so-called equations of congruence. These equations are obtained by eliminating the redundant constraints, replacing them with the constraint reactions exerted by them and imposing the abeyance of the constraints that have been eliminated. The procedure presupposes that the strains and displacements, produced both by the external loading and by the reactions of the constraints that have been eliminated, are known. A simple example may suffice to illustrate these concepts.

Figure 1.1

Figure 1.2

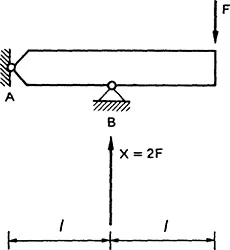
Let us consider a bar hinged at point A and supported at point B, subjected to the end force F (Figure 1.1). The reaction X produced by the support Β is obtained by imposing equilibrium with regard to rotation about hinge A:

F(2l)=Xl⇒X=2F

1.1

The equation of equilibrium with regard to vertical translation provides, on the other hand, the reaction of hinge A. The problem is thus statically determinate or isostatic.

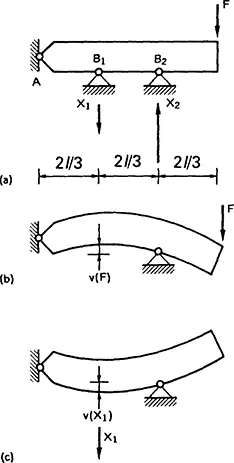
Let us now consider the same bar hinged, not only at A but also at two points Β₁ and B₂, distant 23l and 43l respectively from point A (Figure 1.2 (a)). The condition of equilibrium with regard to rotation gives us an equation in two unknowns:

F(2l)=Xl23l=X243l

1.2

Thus the pairs of reactions X₁ and X₂ which ensure rotational equilibrium are infinite, but only one of these also ensures congruence, i.e. abeyance of the conditions of constraint. The vertical displacement both in B₁ and B₂ must in fact be zero.

To determine the constraint reactions, we thus proceed to eliminate one of the two hinges B₁ or B₂, for example B₁, and we find out how much point B₁ rises owing to the external force F (Figure 1.2(b)) and how much it drops owing to the unknown reaction X₁ (Figure 1.2(c)). The condition of congruence consists of putting the total displacement of B₁ equal to zero:

v(F)=v(X1)

1.3

The equation of equilibrium (1.2) and the equation of congruence (1.3) together solve the problem, which is said to be statically indeterminate or hyperstatic.

1.2 Classification of structural elements

As has already been mentioned in the preliminary remarks, the structural elements which combine to make up the load-bearing structures of civil and industrial buildings, as well as any naturally occurring structure such as rock masses, plants or skeletons, can fit into one of three distinct categories:

1. one-dimensional elements (e.g. ropes, struts, beams, arches);
2. two-dimensional elements (e.g. membranes, plates, slabs, shells, vaults);
3. three-dimensional elements (stubby solids).

In the case of one-dimensional elements, for example beams (Figure 1.3), one of the three dimensions, the length, is much larger than the other two, which compose the cross section. Hence, it is possible to neglect the latter two dimensions and consider the entire element as concentrated along the line forming its centroidal axis. In our calculations, f...