Basic Mechanics with Engineering Applications

J Jones, J Burdess, J Fawcett

• Publisher: Routledge
• Year: 2012
• ISBN:
  9781136076299
• Edition: 1
• Topic: Éducation
• Subtopic: Éducation générale

This book gives a sufficient grounding in mechanics for engineers to tackle a significant range of problems encountered in the design and specification of simple structures and machines. It also provides an excellent background for students wishing to progress to more advanced studies in three-dimensional mechanics.

1

Kinematics

Basic Theory

1.1 Vector quantities

Postion, velocity and acceleration cannot be described solely in terms of magnitude; their directions must also be specified. Quantities which require a definition of both magnitude and direction are called vector quantities; those defined by magnitude only are referred to as scalar quantities. Heavy type will be used to denote a vector, e.g. r is a vector with magnitude r. (A straight line above the symbol, or a wavy line beneath are alternative methods of notation.) A vector quantity is represented graphically by the line and arrow head shown in Fig. 1.1. The length of the line is proportional to the magnitude of the vector and the direction is specified by the orientation of the line and the direction of the arrowhead.

The addition and multiplication of vectors must be carried out according to the rules of vector algebra. For the purposes of this elementary text, which is restricted to the study of motion in a plane, we need only consider the rules of vector addition.

Vector addition

The sum c of two vectors a and b is defined by the diagonal OC of the parallelogram OABC of Fig. 1.2. The lines OA, OB represent the vectors a and b in both magnitude and direction. Upon completion of the parallelogram, its diagonal OC represents the sum, or resultant, of a and b. This method of addition is referred to as the parallelogram rule of vector addition. The length OC and its direction may be obtained by drawing the parallelogram to some convenient scale, or from simple geometry.

We represent the addition of two vectors by the vector equation

c = a + b

where the heavy type indicates that we require a vector sum, as given by the parallelogram rule, rather than the usual scalar sum involving magnitude alone.

An equivalent and more convenient method of adding two vectors is to draw the first vector a, and then the second vector b starting from the tip of vector a, as in Fig. 1.3. The sum, or resultant, c will be the vector from the tail of a to the tip of b and will close the triangle. This is identical to ΔOAC of Fig. 1.2. We could of course have started with the vector b and then added a. This would be equivalent to ΔOBC of Fig. 1.2. The order of the addition is therefore seen to be unimportant, i.e. a + b = b + a.

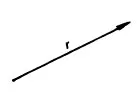
FIG. 1.1

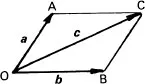
FIG. 1.2

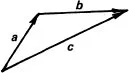
FIG. 1.3

If we wish to add more than two vectors we may extend the above method. For example, to add the four vectors a, b, c and d the sum or resultant e can be obtained by placing them tip to tail as in Fig. 1.4(a), i.e. e = a + b + c + d.

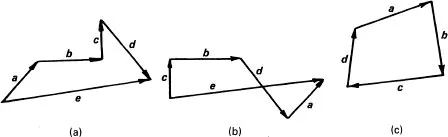
FIG. 1.4

The order can be seen to be unimportant if we recombine them as in Fig. 1.4(b) where e = c + b + d + a.

If the vectors being added form a closed polygon the length of the resultant will be zero, as in Fig. 1.4(c), and their vector sum will be zero, i.e. a + b + c + d = 0.

Components of a vector

It is often convenient to consider a vector in terms of two mutually perpendicular vectors whose sum is equal to the original vector. In Fig. 1.5 the vector c is the sum of the two vectors a and b which...