Philosophy in America

Max Black

• Publisher: Routledge
• Year: 2014
• ISBN:
  9781317853459
• Edition: 1
• Topic: Filosofía
• Subtopic: Historia y teoría filosóficas

This is Volume V of twenty-two of a collection on 20th Century Philosophy. Originally published in 1964, this collection contains original papers assembled and representative in their styles, methods, and preoccupations. The various problems here discussed where to the author both important and unsolved: if others are stimulated to make further progress in solving them, the main purpose of this collection will have been achieved.

IX
FREGE’S THEORY OF NUMBER

by CHARLES D. PARSONS

Associate Professor of Philosophy, Columbia University

It is impossible to compare Frege’s Foundations of Arithmetic¹ with the writings on the philosophy of mathematics of Frege’s predecessors—even with such great philosophers as Kant—without concluding that Frege’s work represents an enormous advance in clarity and rigour. It is also hard to avoid the conclusion that Frege’s analysis increases our understanding of the elementary ideas of arithmetic and that there are fundamental philosophical points that his predecessors grasped very dimly, if at all, which Frege is clear about.

I mention this impression which Frege’s book makes because it is often forgotten in critical discussion of his ideas, and still more forgotten in discussion of ‘the Frege—Russell view’, ‘the reduction of mathematics to logic’, or ‘logicism’. Frege’s main thesis, that arithmetic is a part of logic, is not fashionable now. It seems to me that this is justified, and the accumulated force of the criticisms of this thesis is overwhelming. But even though Frege is more studied now than at the time when his thesis was regarded by many as having been conclusively proved, I find that we still lack a clear view of what is true and what is false in his account of arithmetic. What follows is intended as a contribution toward such a view.

It will help with this task not to focus our attention too exclusively on the thesis that arithmetic is a part of logic. An examination of the argument of the Foundations shows that this thesis is introduced only after some of the confusions of his predecessors have been cleared up by other analyses. It seems to me that we might best divide Frege’s view into three theses, which I shall discuss in turn.

(1) Having a certain cardinal number is a property of a concept in what we may take to be Frege’s technical sense. It appears that the basic type of singular term referring to numbers is of the form ‘the number of objects falling under the concept F’, or, more briefly, ‘the number of F’s’, or in symbolic notation ‘N_x Fx’.

(2) Numbers are objects—again in Frege’s technical sense.

(3) Arithmetic is a part of logic. This may be divided into two:

(a) The concepts of arithmetic can be defined in terms of the concepts of logic.

(b) The theorems of arithmetic can be proved by means of purely logical laws.

The first thesis does not require much discussion. The appeal to Frege’s special sense of ‘concept’ is of course something which would give rise to difficulty and controversy, but it is not essential to the main point. Everyone will agree that we cannot get far in talking about cardinal numbers without introducing singular terms of the form mentioned, or others in which the general term is replaced by a term referring to a class or similar entity.

There is a further question whether, in elementary examples involving perceptual objects, we could attribute the number to something more concrete, or more in accord with the demands of nominalism, than a class or a concept. Frege himself was apparently not interested in this question, and it does not seem to me very important for the foundations of mathematics.

I shall now discuss the thesis that numbers are objects. It will prove to be closely connected with the third thesis, that arithmetic is a part of logic. The first thing to note is that for Frege the notion of an object is a logical one. He held that linguistic expressions satisfying certain syntactical conditions at least purport to refer to objects. I do not have a precise general account of what these conditions are. Being a possible subject of a proposition is the primary one, but it must be so in a logical sense; otherwise ‘every man’ in ‘Every man is mortal’ would refer to an object. The occurrence of the definite article is an important criterion. Such examples as ‘The number 7 is a prime number’ seem to show that numerical expressions satisfy the syntactical criteria.

Another criterion of great importance in the Foundations is that identity must have sense for every kind of object.

Frege took this in a very strong sense: if we think of ‘_ _ _’ and ‘….’ as object-expressions, then ‘_ _ _ = …’ must have sense even if the objects to which they purport to refer are of quite different categories, for example, if ‘_ _ _’ is ‘the Moon’ and ’….’ is ‘the square root of 2’.¹ Moreover, the principle of substitutivity of identity must be satisfied.

Now for every object there is one type of proposition which must have a sense, namely the recognition-statement, which in the case of numbers is called an identity. … When are we entitled to regard a content as that of a recognition-judgement? For this a certain condition has to be satisfied, namely that it must be possible in every judgement to substitute without loss of truth the right-hand side of our putative identity for its left-hand side.²

This is a view which Quine expresses succinctly by the maxim, ‘No entity without identity’. One of the main efforts of the positive part of the Foundations is to explain the sense of identities involving numbers.

That terms satisfying these conditions, and perhaps others besides, occur in places accessible to quantification, and that we make such inferences as existential generalization (e.g. from ‘2 is an even prime number’ to ‘There is an even prime number’) might be taken to show that numerical terms purport to refer to objects. From Frege’s point of view, however, I should think that this shows only that they purport to refer, for quantification could also occur over functions, including concepts.

Shall we accept Frege’s criteria for expressions to purport to refer to objects? We might, I think, separate those explicitly stated by Frege from the criterion, added from Quine, of accessibility to quantification. The latter has some complications having to do with mathematical constructivity and predicativity. These do not make it an unacceptable criterion, but might lead us to distinguish ‘grades of referential involvement’. With this reservation, I do not know any better criteria than the ones I have mentioned. I am still not very clear about their significance, what it is to be an object. In particular, the central role of identity is something which I do not know how to explain. Perhaps it has to do with the fact that the cognitive activities of human beings are spread out over space and time.

I have been very careful to speak of criteria for expressions to purport to refer to objects. Indeed, it would seem that if we explain number-words in such a way that they will be shown in at least some of their occurrences to satisfy these criteria, then we shall at most have shown that they purport to refer to objects but not that they actually do refer to them, i.e. that in these occurrences they actually have reference. I shall now consider how this matter stands in Frege’s analysis of number.

The simplest account of it is as follows: Frege finds¹ that a necessary and sufficient condition for the number of F’s to be the same as the number of G’s is that the concept F and the concept G stand in a relation he called Gleichzahligkeit, which may be translated as ‘numerical equivalence’. The concept F is numerically equivalent to the concept G if there is a one-to-one correspondence of the objects satisfying F and the objects satisfying G. If we express this by ‘Glz_x(Fx, Gx)’, we may express the result of this stage of Frege’s analysis as the principle

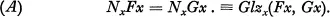
He then gives an explicit definition whose initial justification is that (A) follows from it. The number of F’s is defined as the extension of the concept numerically equivalent to the concept F, in other words the class of all concepts numerically equivalent to the concept F.

Then it seems that the problem of the existence of numbers is merely reduced to the problem of the existence of extensions. If this is so, Frege is in two difficulties.

The first is that the paradoxes make it not very clear what assumptions as to the existence of extensions of concepts are permissible. Frege sought a general logical law by which one could pass from a co...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Preface
• Table of Contents
• I Expressing
• II On the Complexity of Avowals
• III Must Every Inference Be Either Deductive or Inductive?
• IV Aesthetic Problems of Modern Philosophy
• V Seeing Surfaces and Physical Objects
• VI Aesthetic Essence
• VII Action and Responsibility
• VIII Explanations in Psychology
• IX Frege's Theory of Number
• X The Free Will Defence
• XI What is a Speech Act?
• XII Quantum Physics and the Philosophy of Whitehead
• XIII Predicability
• XIV Reasons and Reasoning
• Index of Names