Superportraits

Caricatures and Recognition

Gillian Rhodes

• Publisher: Psychology Press
• Year: 1997
• ISBN:
  9781135472375
• Edition: 1
• Topic: Psychology
• Subtopic: History & Theory in Psychology
• Index: Psychology

As Nixon's unpopularity increased during Watergate, his nose and jowls grew to impossible proportions in published caricatures. Yet the caricatures remained instantly recognizable. Caricatures can even be superportraits, with the paradoxical quality of being more like the face than the face itself.
How can we recognize such distorted images? Do caricatures derive their power from some special property of a face recognition system or from some more general property of recognition systems? What kind of mental representations and recognition processes make caricatures so effective? What can the power of caricatures tell us about recognition?
In seeking to answer these questions, the author assembles clues from a variety of sources: the invention and development of caricatures by artists, the exploitation of extreme signals in animal communication systems, and studies of how humans, other animals and connectionist recognition systems respond to caricatures.
Several conclusions emerge. The power of caricatures is ubiquitous. Caricatures can be superportraits for humans, other animals and computer recognition systems. They are effective for a variety of stimuli, not just faces. They are effective whether objects are mentally represented as deviations from a norm or average member of the class, or as absolute feature values on a set of dimensions. Exaggeration of crucial norm-deviation features, distinctiveness, and resemblance to caricatured memory traces are all potential sources of the power of caricature.
Superportraits will be of interest to students of cognitive psychology, perception, the visual arts and animal behavior.

CHAPTER ONE
Introduction

…an object that is novel and yet similar to an already significant object may especially warrant our close attention. We need to know how far something can depart from its usual or expected form and still have the consequences that we have found to follow from its “natural kind”. In doing so, we also come closer to an understanding of the critical features of a stimulus that elicits a resonant response within us and, thus, closer to an understanding of ourselves.

Shepard (1990) p.202

THE CHALLENGE OF CARICATURES

As Nixon’s popularity plummeted during Watergate, his nose and jowls grew to impossible proportions in published caricatures. Yet the caricatures remained instantly recognisable. In some cases caricatures are even superportraits, with the paradoxical quality of being more like the face than the face itself. As one viewer of a television programme featuring caricatured puppets exclaimed, “Hell the one of Bill Cosby looks more like Bill Cosby than Bill Cosby does!”.

The power of caricatures sets a challenge for those of us who are interested in how recognition works. How can such obviously distorted images be more recognisable than undistorted images? Indeed, how can they be recognised at all? Do caricatures exploit some special property of a face recognition system, or are they effective for a variety of objects, capitalising on some more fundamental preference for exaggeration? These are the kinds of questions that I will address in this book. Along the way I will also explore the role of exaggeration in art and nature, looking for clues about the kind of mental representations and recognition processes from which caricatures might derive their power.

RECOGNITION

Before turning the spotlight onto caricatures, let me begin with some background about recognition. The ability to recognise objects by their appearance supports an enormous range of activities. It allows us to find food, to avoid predation, to orient ourselves using landmarks, to recognise people, and to maintain a complex network of social interactions.

Recognition occurs automatically and without conscious effort, but it is no mean feat. In order to recognise what we see, we must convert the complex, but ephemeral, patterns of light energy reaching our eyes into stable, familiar, and meaningful representations. To recognise objects the visual system must solve two problems. The first is caused by the huge variety of appearances that an object can present due to changes in our viewpoint.¹ To recognise an object we must be able to map a potentially infinite set of images onto a single object representation, i.e. we must solve the object constancy problem.

The second problem stems from the extreme similarity of objects like faces. Our expertise with faces can blind us to their similarity, but you can get some idea if you look at your old school photographs upside-down, or visit an exotic location where faces are different from those you are used to seeing. Humpty-Dumpty put his finger on the nature of the difficulty, when he complained to Alice that, “You’re so exactly like other people…the two eyes, so (marking their places in the air with his thumb) nose in the middle, mouth under. It’s always the same. Now if you had the two eyes on the same side of the nose, for instance—or the mouth at the top—that would be some help.” (Carroll, 1946). As Humpty-Dumpty observed, faces are difficult to recognise precisely because they have the same basic parts in the same basic arrangement, i.e. because of their homogeneity. Therefore, in order to recognise faces and other objects that share a configuration (birds, dogs, cars, etc.) our visual system must find a way of representing the subtle differences that distinguish such similar objects, i.e. it must solve the homogeneity problem.

We know that the visual system has solved these two problems. After all, we routinely recognise familiar objects from different viewpoints and homogeneous objects such as faces. What is less clear is how we solve these problems. Let’s consider each one in turn.

Solving the object constancy problem

The object constancy problem could potentially be solved in a variety of ways. One way would be to use view-independent representations that don’t change with changes in viewpoint. Marr (1982) developed this idea, suggesting that the arrangement of an object’s parts is described in relation to the main axis of elongation of the object. This axis defines a co-ordinate system, or frame of reference, within which the rest of the parts can be described and located. By describing the object’s structure using a co-ordinate system centred on the object itself, the representation does not change with the viewer’s perspective.

Another kind of view-independent representation can be obtained by describing the object’s structure without reference to any co-ordinate system at all. Biederman (1987, 1990) developed this idea, proposing that we represent objects using a limited vocabulary of simple 3-D shapes called geons. Geons are created by sweeping a cross-sectional shape, like a circle or square, along an axis, and they can be defined by properties that don’t change with the observer’s viewpoint, such as the curvature, symmetry, and size of the cross-section, and the curvature of the axis. In both cases the perceptual representation can be compared with stored representations of the same type, and recognition occurs when a match is found. Viewpoint-invariant representations seem to offer an elegant and economical solution to the object constancy problem. They are unaffected by changes in one’s viewpoint, and only a single representation must be stored for each object. However, they may be difficult or impossible to derive from images. Marr offered no algorithm that could detect the axis of elongation, and some objects do not even have one (e.g. crumpled newspaper, beach balls). Nor is it clear just how successfully geons can be derived from images. Therefore, the economy of storage and ease of matching offered by viewpoint-invariant representations may come at a high computational price, i.e. they are difficult to compute from images.

An alternative solution to the object constancy problem would be to use view-specific representations, such as descriptions in retinal co-ordinates. These are much easier to derive from images than view-invariant representations. However, the matching process is more demanding. Unless an enormous set of viewpoints is stored for every object, some transformation (e.g. mental rotation, Tarr & Pinker, 1989; alignment, Ullman, 1989) will be needed to map a perceptual representation onto the stored descriptions for each familiar object. The set of stored descriptions for an object might consist of a single representation, such as a commonly seen view or a canonical view that shows the most salient features or parts of the object. Alternatively, it might consist of a small set of viewpoints, such as those experienced most frequently or those that display qualitatively different information about the object (e.g. handle-present and handle-absent views of a cup, Koenderink & Van Doorn, 1979).

The relative merits of view-specific and view-independent representations are currently the subject of intensive debate (Biederman, 1995; Biederman & Gerhardstein, 1993, 1995; Corballis, 1988; Rock & Di Vita, 1987; Takano, 1989; Tarr & Bülthoff, 1995; Tarr, Hayward, Gauthier, & Williams, 1994; Tarr & Pinker, 1989, 1990; Ullman, 1989). In addition to the problem of how view-independent representations can be derived from images, those who favour this solution to the object constancy problem must also explain why the orientation of an object, especially orientation in the picture plane, consistently affects recognition performance (e.g. Jolicoeur, 1985; Rock & Di Vita, 1987; Tarr & Pinker, 1989, 1990). After all, the whole point of viewpoint-independent representations is that they are unaffected by such changes in the image. The debate remains unresolved, although some authors have recently suggested a compromise solution, with both types of representation used, but each under different circumstances (e.g. Corballis, 1988; Jolicoeur, 1990; Tarr & Chawarski, 1993). For example, view-invariant representations may be used when the arrangement of parts in a 2-D object differs on a single dimension, but not when it differs on more than one dimension (Tarr & Pinker, 1990).

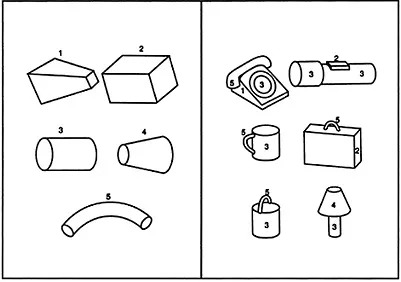
There is considerable agreement² that objects are represented by their component parts and the overall spatial arrangement of those parts (Biederman, 1987; Hoffman & Richards, 1984; Marr, 1982) (see Fig. 1.1). A part-based representation is ideal for basic level recognition (Rosch, Mervis et al., 1976)—chair, car, house, dog, tree, etc.—because basic level objects, especially manufactured ones (Corballis, 1991), differ primarily in their parts (Tversky & Hemenway, 1984) and the spatial arrangement of those parts (Biederman, 1987).

However, such a system will not work for all objects. In particular, it won’t work for homogeneous objects like faces that have the same basic components in the same basic arrangement. A part-based analysis can tell us that we’re looking at a face, but not whose face it is. To recognise an individual face, something subtler than a parts-analysis is needed, something that capitalises on the subtle variations within the shared configuration that are unique to each face.

FIG. 1.1. The part-based structure of
common objects is illustrated in this
figure from Biederman (1990).
Examples of geons (volume
primitives) are shown on the left. The
identity and arrangement (cf. cup and
bucket) of geons in some common
objects are shown on the right.
Reproduced with permission from
Biederman (1990).

Solving the homogeneity problem

Diamond and Carey (1986) have sought a solution to the homogeneity problem by considering the constraints imposed by the stimuli themselves. They proposed a continuum of features ranging from relatively isolated to relatively relational features.³ These features could be anything that is used to distinguish faces. Isolated features can be specified without reference to several parts of the stimulus at once. Examples are the presence and shape of glasses, facial hair, scars, or wrinkles, as well as non-spatial cues like hair colour and texture. Relational features, in contrast, cannot be specified without reference to several parts of the face at once. Examples include ratios of distances and the internal spacing of features.

Although a few faces have distinctive isolated features such as a handlebar moustache or a tell-tale scar, isolated features will not generally suffice for distinguishing the hundreds or even thousands of faces that we can each recognise. Instead, Diamond and Carey suggested that relational features are crucial for face recognition. Moreover, they conjectured that reliance on relational features makes face recognition unusually vulnerable to inversion. Turning faces upside-down disrupts recognition much more than turning other mono-oriented objects upside-down, with accuracy dropping 20–30% for faces compared with 0–10% for other objects (Carey & Diamond, 1994; Diamond & Carey, 1986; Rhodes et al., 1993; Valentine, 1988; Yin, 1969, 1970). Recognition of complex stimuli like landscapes that do not share a configuration is not especially disrupted by inversion, so that a large inversion decrement seems to be a feature of homogeneous objects.

This proposed link between reliance on relational features and large inversion decrements has been confirmed recently. Changes to relational features (e.g. the spacing of the internal features of eyes, nose, and mouth) are more difficult to detect than changes to isolated features (e.g. glasses or moustache) in inverted faces (Rhodes et al., 1993). Similarly, James Bartlett and Jean Searcy (Bartlett, 1994; Bartlett & Searcy, 1993; Searcy & Bartlett, in press) have shown that faces made to look grotesque by changing the spatial relations between parts no longer look grotesque when inverted, whereas faces whose grotesqueness depends on isolated feature cues (e.g. fangs added, eyes reddened) continue to look grotesque when inverted. These results support Diamond and Carey’s claim that large inversion decrements are a hallmark of relational feature coding.

The most extreme form of relational feature coding is holistic coding, in which there is no explicit representation of parts at all. Perhaps faces are represented more holistically than other objects (Corballis, 1991; Farah, 1992; Farah, Tanaka, & Drain, 1995; Tanaka & Farah, 1993). If parts are not explicitly represented then they should be difficult to recognise in isolation. Therefore, the finding that parts are recognised better when presented in the whole object than in isolation, for faces but not for scrambled faces, inverted faces, or houses (Tanaka & Farah, 1993), suggests that upright faces are coded more holistically than these other classes of objects. Forcing people to code faces in terms of their parts, by presenting the head outline, eyes, nose, and mouth in separate frames, also eliminates the inversion decrement for faces (Farah et al., 1995). Farah and her colleagues therefore suggest that the disproportionate inversion decrement normally found for face recognition reflects holistic coding.

These results, however, are also consistent with the idea that relational features are crucial for face recognition. In the first case, the relationships between a target part and the rest of the face will be disrupted when that part is presented in isolation. In the second case, relational features will be difficult to code when the parts of a face are shown in separate frames. It should not be surprising if holistic and relational coding prove difficult to distinguish experimentally, because holistic coding is really an extreme form of relational coding.

Faces provide the most dramatic illustration of the homogeneity problem, but the ability to code variations in a shared configuration would be useful in many discriminations, ranging from biologically significant discriminations between different kinds of animals and plants, to more mundane discriminations between different cars or chairs. Therefore, relational coding could be part of a general solution to the homogeneity problem. Alternatively, it might be part of a special system dedicated to face recognition (for further discussion see Farah, 1992; Rhodes, 1994, 1996).

The idea that faces might be special has considerable appeal. There are neural areas dedicated to face recognition, damage to which results in prosopagnosia, a remarkably specific inability to recognise faces (for reviews see Damasio, Tranel & Damasio, 1990; de Renzi, 1986; Farah, 1990). The importance of faces may have generated considerable selection pressure for an efficient face recognition system, and evolution certainly seems to have equipped neonates with a built-in interest in faces (for a review see Johnson & Morton, 1991). Finally, the unusual homogeneity of faces may demand a special-purpose system for successful recognition.

Despite the plausibility of the idea, however, there is no evidence for a processing system that deals exclusively with faces (e.g. Diamond & Carey, 1986; Davidoff, 1986; Ellis & Young, 1989; Farah, 1992; Levine, 1989; Morton & Johnson, 1989; Rhodes, 1996). In particular, the coding of relational information that is so important for face recognition is not unique to faces. Diamond and Carey (1986) found an inversion decrement for recognising whole body profiles of dogs that was as large as the decrement for face recognition. The large inversion decrement for dog recognition was confined to dog experts, suggesting that expertise is needed to use relational features, presum...