Theory of Transformations in Steels

Harshad K. D. H. Bhadeshia

• Publisher: CRC Press
• Year: 2021
• ISBN:
  9781000352764
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Mechanics

Written by the leading authority in the field of solid-state phase transformations, Theory of Transformations in Steels is the first book to provide readers with a complete discussion of the theory of transformations in steel.

• 
  
  

• Offers comprehensive treatment of solid-state transformations, covering the vast number in steels

• 
  
  

• Serves as a single source for almost any aspect of the subject

• 
  
  

• Features discussion of physical properties, thermodynamics, diffusion, and kinetics

• 
  
  

• Covers ferrites, martensite, cementite, carbides, nitrides, substitutionally-alloyed precipitates, and pearlite

• 
  
  

• Contains a thoroughly researched and comprehensive list of references as further and recommended reading

With its broad and deep coverage of the subject, this work aims at inspiring research within the field of materials science and metallurgy.

1Crystal structures and mechanisms

1.1 Allotropes of Iron

Why do metals adopt the crystal structures that they do? This no longer is a curiosity because the metallic state is so well understood that it is possible to select, from a calculation of the cohesive energies of trial structures, that which should be the most stable. Figure 1.1 shows the cohesive energy as a function of the density and crystal structure. Of all the test structures, hexagonal close-packed (hcp) iron is found to have the highest cohesion and therefore should represent the most stable form. This contradicts experience, but the calculations do not account for the ferromagnetism of body-centred cubic iron (ferrite), which would make it more stable than the hcp form. There are in fact magnetic transitions in each of the allotropes of iron, details of which are reserved for Chapter 2.

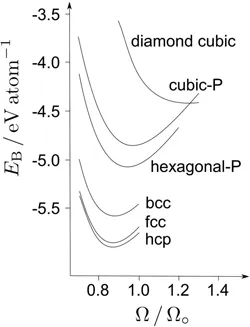
Figure 1.1 Plot of cohesive energy $E_{\text{B}}$ for 0K and 0Pa pressure versus the normalised volume per atom for a variety of crystal structures of iron. $E_{\text{B}}$ is the binding energy per atom in the crystal relative to that of a free atom. Hexagonal-P and Cubic-P are primitive structures; like the diamond cubic form, they do not exist on earth. Adapted with permission from [1]. Copyrighted by the American Physical Society.

Only three allotropes of iron occur in nature, in bulk form; Figure 1.2 shows the phase diagram for pure iron. Each point on a boundary between the phase fields represents an equilibrium state in which two phases can coexist. The triple point where the three boundaries intersect represents an equilibrium between all three co-existing phases. It is seen that in pure iron, the hexagonal close-packed form is stable only at high pressures, consistent with its high density.

There are two further allotropes which can be created in the form of thin films. Face-centred tetragonal iron can be prepared by coherently depositing iron as a thin film on a $\left\{100\right\}$ plane of a substrate such as copper with which the iron has a mismatch. The atoms in the first deposited layer replicate the positions of those on the substrate. A few monolayers can be forced into coherency in the plane of the substrate with a corresponding distortion normal to the substrate. This gives the deposit a face-centred tetragonal structure which in the absence of any mismatch would be face-centred cubic [2, 3]. Eventually, as the film thickens during the deposition process to beyond about ten monolayers (on copper), the structure relaxes to the low-energy bcc form, a process accompanied by the formation of dislocation defects which accommodate the misfit with the substrate.

Growing iron on a misfitting $\left\{111\right\}$ surface of a face-centred cubic substrate similarly causes a distortion along the surface normal, giving trigonal iron [4].¹ Graphene is a single layer of carbon atoms that has a hexagonal structure with a lattice parameter of 0.245nm. The crystal is seldom perfect, often containing holes. Compounds used in its manufacture provide a source of iron atoms that can attach themselves to the edges of these holes, building up into monoatomic layers that are suspended in the graphene films. These “free-standing” single-atom-thick two-dimensional arrays of iron form a square lattice with a parameter 0.265 $\pm 0.005$ nm [5]. This particular structure has been suggested to be a consequence of lattice matching with the “armchair” configuration of carbon atoms at the graphene edges where the bonding between the iron and carbon atoms is stronger than when the iron attaches to the “zig-zag” edges of the graphene [5]. The largest stable monolayer of iron on holes in graphene is found to be about 3nm² in area.

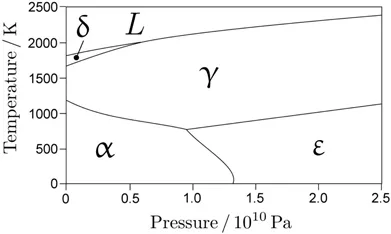
Figure 1.2 Temperature versus pressure equilibrium phase diagram for pure iron, based on assessed thermodynamic data. The triple point temperature and pressure are 490^∘C and 11GPa respectively. $\alpha$, $\gamma$ and $\epsilon$ refer to ferrite, austenite and $\epsilon$-iron respectively. δ is simply the higher temperature designation of $\alpha$. Diagram courtesy of Shaumik Lenka, calculated using the database ‘TCFE8’, and ThermoCalc version 2015b.

Table 1.1 lists some transformation temperatures and thermodynamic data for the natural allotropes of iron. The free energy changes during the solid-state transformations are really quite small, even when compared with the energy associated with the magnetic disordering of ferrite. In a way, this is a reflection of the fact that their crystal structures are not all that different (Figure 1.3). For example, assuming a hard-sphere model, the crystal structure of austenite and $\epsilon$-iron can be generated by stacking close-packed layers of iron atoms in such a way that each successive layer sits in the depressions of the underlying layer. There are in each layer, two types of depressions, so the close-packed layers can be stacked either in the sequence $\dots ABCABCABC\dots$ or $\dots ABABABABA\dots$. The former sequence, which has a stacking period of three, generates the austenite structure, whereas the latter gives the hcp structure of $\epsilon$-iron with a stacking period of two. The best comparison of the relative densities of the phases is made at the triple point where the allotropes are in...

Table of contents

• Cover
• Half Title
• Title
• Copyright
• Dedication
• Contents
• Preface
• Author
• Acronyms etc.
• Nomenclature
• Chapter 1 Crystal structures and mechanisms
• Chapter 2 Thermodynamics
• Chapter 3 Diffusion
• Chapter 4 Ferrite by reconstructive transformation
• Chapter 5 Martensite
• Chapter 6 Bainite
• Chapter 7 Widmanstätten ferrite
• Chapter 8 Cementite
• Chapter 9 Other Fe-C carbides
• Chapter 10 Nitrides
• Chapter 11 Substitutionally alloyed precipitates
• Chapter 12 Pearlite
• Chapter 13 Aspects of kinetic theory
• Author index
• Subject index