Princeton Puzzlers

The Mathematics of Chessboard Problems

John J. Watkins

• Publisher: Princeton University Press
• Year: 2011
• ISBN:
  9781400840922
• Topic: Mathematics
• Subtopic: Games in Mathematics
• Index: Mathematics

Across the Board is the definitive work on chessboard problems. It is not simply about chess but the chessboard itself--that simple grid of squares so common to games around the world. And, more importantly, the fascinating mathematics behind it. From the Knight's Tour Problem and Queens Domination to their many variations, John Watkins surveys all the well-known problems in this surprisingly fertile area of recreational mathematics. Can a knight follow a path that covers every square once, ending on the starting square? How many queens are needed so that every square is targeted or occupied by one of the queens?
Each main topic is treated in depth from its historical conception through to its status today. Many beautiful solutions have emerged for basic chessboard problems since mathematicians first began working on them in earnest over three centuries ago, but such problems, including those involving polyominoes, have now been extended to three-dimensional chessboards and even chessboards on unusual surfaces such as toruses (the equivalent of playing chess on a doughnut) and cylinders. Using the highly visual language of graph theory, Watkins gently guides the reader to the forefront of current research in mathematics. By solving some of the many exercises sprinkled throughout, the reader can share fully in the excitement of discovery.
Showing that chess puzzles are the starting point for important mathematical ideas that have resonated for centuries, Across the Board will captivate students and instructors, mathematicians, chess enthusiasts, and puzzle devotees.

CHAPTER ONE

Introduction

We are no other than a moving row

Of Magic Shadow-shapes that come and go

Round with the Sun-illumined Lantern held

In Midnight by the Master of the Show;

But helpless Pieces of the Game He plays

Upon this Chequer-board of Nights and Days;

Hither and thither moves, and checks, and slays,

And one by one back in the Closet lays.

Omar Khayyám, The Rubáiyát

This book is about the chessboard. No, not about chess, but about the board itself. The chessboard provides the field of play for any number of games, both ancient and modern: chess and its many variants around the world, checkers or draughts, Go, Snakes and Ladders, and even the word game Scrabble. Boards for these games come in many sizes: 8 × 8 boards for chess; 8 × 8 and 10 × 10 boards for checkers, depending on what part of the world you are in; 10 × 10 boards for Snakes and Ladders; 15 × 15 boards for Scrabble; 18 × 18 boards for Go; and even non-square sizes such as 4 × 8 and 2 × 6 boards for Bau and Owari, two games that are widely played in various forms and under several different names in Africa.

In some board games there are no special colors given to individual squares of the board, all squares are the same, but in other games the color of individual squares can be very important. The familiar checkered black and white or black and red alternating coloring of the squares in chess or checkers are the best examples of this. Alfred Butts spent years during the 1930s and 1940s tinkering with the coloring of the board for the game that eventually became Scrabble, deliberating on exactly where the double and triple valued squares should go, what their colors should be, and how many of each type he wanted. We, too, will discover that ingenious colorings of the squares on an otherwise ordinary chessboard can pay surprising dividends.

Board games, like other of our games, are usually in some form a metaphor for life itself. Chess, of course, is about war, conquering your enemy and protecting your king; Go is about the territorial imperative; Snakes and Ladders a morality play for children about how to achieve Nirvana. Omar Khayyám, in the two quatrains I quoted for you from The Rubáiyát, saw in such games a reflection of our lives as mere ‘pawns’ in a game run by the ‘Master of the Show’, a theme picked up by Shakespeare 300 years later in As You Like It, the play with which he possibly opened the Globe Theatre in 1599:

All the world’s a stage,

And all the men and women merely players;

They have their exits and their entrances,

And one man in his time plays many parts,

His acts being seven ages.

Even now, in an age, and especially in a society, such as ours, in which the problematic notion of free will is simply taken for granted, this is still an idea that carries a chilling weight.

However, this is not a book about such games, and still less is this book concerned with the cultural significance of the games we humans play. Instead, this book is about the game board itself, the simple grid of squares that forms such a common feature of games played around the world, and, more importantly, about the mathematics that arises from such an apparently simple structure. Let us begin with a puzzle.

GUARINI’S PROBLEM

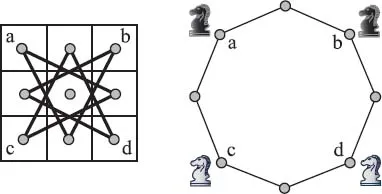
The earliest chessboard puzzle that I know of dates from 1512, almost 500 years ago. This puzzle is known as Guarini’s Problem and involves four knights, two white and two black, at the four corners of a small 3 × 3 chessboard. The white knights and the black knights wish to exchange places. Their situation is shown in Figure 1.1. A knight can move on a chessboard by going two squares in any horizontal or vertical direction, and then turning either left or right one more square. Since, in this problem, each knight will have only two moves available from any position, this is a very simple puzzle to solve, even by trial and error. Still, it is somewhat harder than it might look at first glance, so I urge you to try to do it for yourself before reading on.

Figure 1.1 Guarini’s Problem: switch the knights.

If you solved this problem you undoubtedly observed its underlying basic structure. Note that this rather simple structure comes from two things: the geometry of the board itself along with the particular way in which knights are allowed to move. In Figure 1.2, the structure of the possible knight moves is first exhibited explicitly, on the left, by lines that are drawn to connect any two squares of the board between which a knight can move. This diagram, or graph, can then be ‘unfolded’, as shown on the right in Figure 1.2, and the underlying structure of the graph immediately emerges. The graph, which looked somewhat complicated to us on the left, turns out to consist of only a single cycle, and so the solution to our puzzle is now completely clear. In order to exchange places, the knights have no choice at all. They must march around this cycle, all in the same direction, either clockwise or counterclockwise, until their positions are exactly reversed. This graphical solution, of course, still has to be translated back to the original 3 × 3 chessboard, but this final step is quite straightforward.

Figure 1.2 Ignoring the chessboard and unfolding the graph.

I like Guarini’s Problem in part because it is so very old, but also because it is such a nice illustration of the way in which mathematical abstraction can clear away the messy details of a problem and lead us gently toward a solution. In the case of Guarini’s Problem, the first level of abstraction avoids for us the need to keep worrying about the awkward business of how a knight moves on a chessboard by the simple device of drawing lines on the board to represent these moves. This allowed us to forget about chess completely. The next level of abstraction is to forget also about the actual board and focus instead entirely on the diagram. Then, the final level of abstraction is to eliminate the clutter inherent in the diagram simply by unfolding it. This general process of turning a problem into a diagram is so useful and so natural that an entire area of mathematics, now called graph theory, has evolved that is dedicated to studying the properties and uses of such diagrams, called graphs. This book, then, is really a book about graphs in disguise. Usually, explicit graphs such as the one drawn in Figure 1.2 will be kept offstage during our drama, but rest assured, they are always there and ready to appear at a moment’s notice should we ever have need of them.

Problem 1.1 In Figure 1.3 we now have six knights, three white and three black, on opposite sides of a 4 × 3 chessboard. Find the minimum number of moves required for these knights to exchange places. This variation of Guarini’s Problem appeared in Scientific American in the December 1979 issue. A solution was given the following month. Remember though that you can, if you like, find solutions to these problems at the end of each chapter.

Figure 1.3 Switch the knights.

THE KNIGHT’S TOUR PROBLEM

Since we have just studied a problem involving knights, and we now know how they move, let’s continue with them for the moment. Note that in Guarini’s Problem the center square of the 3 × 3 chessboard is inaccessible to any of the four knights, but that otherwise a single knight could visit each square of the board exactly once and return to its original position merely by making a complete circuit of the cycle graph in Figure 1.2. What about on a larger board, such as a 4×4 board or an 8×8 board, might a knight be able to do a tour of the entire board, that is, visit every square exactly once and return to the start? The answer is: well, sometimes yes, and sometimes no.

The general question of which chessboards have a knight’s tour is known as the Knight’s Tour Problem. This famous problem has a long and rich history. The Knight’s Tour Problem dates back almost to the very beginnings of chess in the sixth century in India and will in fact be one of the main topics considered in this book.

You might wish to try the following problem before continuing further. The key feature of a knight’s tour is that a knight visits each square of the board exactly once. A tour can be closed, meaning the knight returns to its original position, or it can be open, meaning it finishes on a different square than it started. Unless otherwise indicated, the word ‘tour’ in this book will always mean a closed tour.

Problem 1.2 The smallest chessboards for which knight’s tours are possible are the 5 × 6 board and the 3 × 10 board. Find a tour for each of these boards. The smallest board for which an open tour is possible is the 3×4 board. Find an open tour for this board.

Figure 1.4 Find closed tours for the 5 × 6 and the 3 × 10 boards; and an open tour for the 3 × 4 board.

Leonhard Euler, perhaps the most prolific mathematician of all time, did extensive work on the Knight’s Tour Problem. One particularly attractive knight’s tour for the 8 × 8 chessboard, done by Euler in 1759, is shown in Figure 1.5. What is especially interesting about this particular tour is that Euler first does an open tour of the lower half of the board, starting at square 1 and ending at square 32. He then repeats exactly this same tour, in a symmetric fashion, for the upper half of the board, starting at square 33 and ending at square 64. Note that Euler has also very carefully positioned both the beginning and the end of these two open half-tours so that they can be joined together into a tour of the entire chessboard.

This tour of Euler’s tells us something very useful about the Knight’s Tour Problem, at least we now know for sure that the 8 × 8 chessboard has a knight’s tour. On the other hand, we already know that not all chessboards have knight’s tours. For example, as we have seen, ...

Table of contents

• Cover
• Half title
• Title
• Copyright
• Dedication
• Contents
• Preface
• Chapter One Introduction
• Chapter Two Knight’s Tours
• Chapter Three The Knight’s Tour Problem
• Chapter Four Magic Squares
• Chapter Five The Torus and the Cylinder
• Chapter Six The Klein Bottle and Other Variations
• Chapter Seven Domination
• Chapter Eight Queens Domination
• Chapter Nine Domination on Other Surfaces
• Chapter Ten Independence
• Chapter Eleven Other Surfaces, Other Variations
• Chapter Twelve Eulerian Squares
• Chapter Thirteen Polyominoes
• References
• Index