![]()
CHAPTER ONE
Magic Construction
We are in the position of a little child entering a huge library whose walls are covered to the ceiling with books in many different tongues…. The child does not understand the languages in which they are written. He notes a definite plan in the arrangement of books, a mysterious order which he does not comprehend, but only dimly suspects.
– Albert Einstein, The Saturday Evening Post
Categories
When you gaze at magic squares with their amazing properties and hidden symmetries, it’s sometimes difficult to believe that there are easy-to-remember ways to construct many of them using simple rules. In fact, handbooks of “mental magic” often give these methods as “secret” ways to impress audiences.1 The mentalist shows a large, empty square to the enthralled onlookers and, with a flourish and a cry of “voilà!”, creates a magic square with astonishing ease. Imagine yourself being able to write down a large magic square in under a minute in front of an adoring audience. In this chapter, I’ll introduce you to a few methods for constructing some of the traditional magic squares. If you are interested in pursuing the construction of some of the more elaborate magic squares, several books2 in the For Further Reading section provide additional material and food for thought.
Various methods for constructing magic squares have evolved through the ages. When considering these methods, it is useful to categorize magic squares in three classes:
Magic squares of
odd order (squares where the order
N is of the form 2
m + 1, where
m may be any positive integer 1, 2, 3, etc.).
Magic squares of a
doubly even order (where the order
N is of the form 4
m, such as 4, 8, 12, 16, 32, etc.). The order of a doubly even square can be divided by 2 and 4.
Magic squares of a
singly even order (where
N is of the form 2(2
m + 1), such as 2, 6, 10, 14, 18, 22, etc.). The order of a singly even square can be divided by 2 but not 4.
Generation methods for these kinds of squares vary in complexity, and for brevity I focus mostly on magic squares of odd order. Corresponding general methods for the construction of even-order magic squares are difficult to implement with pencil and paper, and magic squares of singly even orders are generally the most difficult of all to construct.
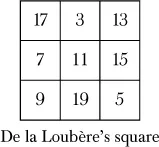
De la Loubère’s Method
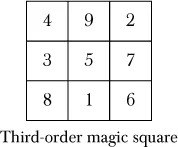
The smallest possible square of an odd order greater than 1 is the third-order square from the Introduction that has only one arrangement if we discount reflections and rotations:
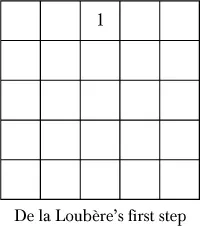
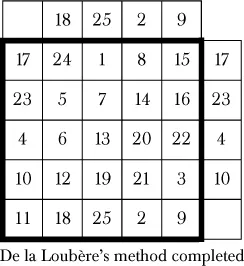
In 1693, mathematician Simon de la Loubère suggested a method to create any odd-order magic square. He learned of it while ambassador to Siam from the court of Louis XIV. You can think of this as the “upward-right method” for reasons that will become clear. Start by placing a 1 in the central upper cell. In this example, we will construct a fifth-order magic square.
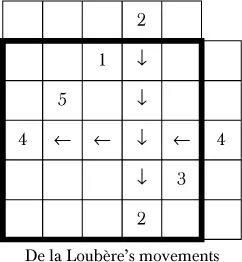
Proceed diagonally upward to the right and place a 2 in an imaginary square outside the table. To visually represent this process, let’s temporarily add another row and column to the square. Because the 2 is outside the square, we bring it to the bottom of the column. Next, write a 3 upward to the right of the 2.
Next, write a 4 upward and to the right of the 3. Because 4 falls outside the original square, place it at the opposite end of the row, and write a 5 upward to the right. We cannot write a 6 upward and to the right of the 5 because the cell is occupied. Therefore, we write the 6 below the 5. We proceed until the 10 falls outside of the original square and continue the process. Notice that 16 falls outside the corner square and is written beneath the 15, as is the case when encountering an occupied square.
In summary
1. Start by placing 1 in the center cell, top row.
2. Whenever a top edge is reached, the integers are continued diagonally upward to the right at the bottom of the next column.
3. When the right-hand edge is reached, the integers are continued at the last cell to the left of the next highest row.
4. When a cell is reached that is already filled, drop down one cell and continue.
5. When the upper right corner cell is reached, drop down one row.
By rotations and reflections, seven other magic squares can be constructed from this method. Once you have memorized this simple approach, you can amaze your friends by generating odd-order squares of higher order. Additionally, you can start with a 1 in any cell and always generate a square that is magic in rows and columns but not necessarily diagonals.
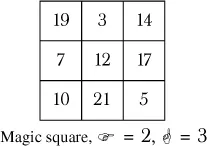
You can also use de la Loubère’s method to form imperfect magic squares that start with numbers other than 1. For example, the following square was created by starting with 3, and each succeeding integer was obtained by adding 2 to the preceding integer:
Try this approach with other starting numbers and with other differences between succeeding integers.
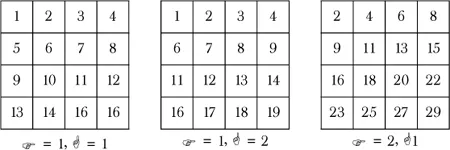
It’s also possible to use de la Loubère’s method to form imperfect magic squares with more complicated number sequences. Let us define the horizontal difference
as the difference between each succeeding integer in each group of
N integers (represented as rows in the following squares). The vertical difference
is defined as the difference between the last integer of the first
N integers and the first integer of the next set of
N integers.
and
do not have to be equal but must remain constant throughout. So you can more easily get a feel for these parameters, here are some examples of
and
in number arrays. (These are not magic squares.)
Here is a magic square created by de la Loubère’s method using a starting number of 3, where
= 2 and
= 3:
In other words, the groups 3, 5, 7; 10, 12, 14; and 17, 19, 21 were used to create this square.
When a magic square of order N is constructed in these ways, it is possible ...