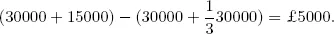Introductory Course on Financial Mathematics

Michael Tretyakov

• Publisher: ICP
• Year: 2013
• ISBN:
  9781908977403
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

This book is an elementary introduction to the basic concepts of financial mathematics with a central focus on discrete models and an aim to demonstrate simple, but widely used, financial derivatives for managing market risks. Only a basic knowledge of probability, real analysis, ordinary differential equations, linear algebra and some common sense are required to understand the concepts considered in this book.

Financial mathematics is an application of advanced mathematical and statistical methods to financial management and markets, with a main objective of quantifying and hedging risks. Since the book aims to present the basics of financial mathematics to the reader, only essential elements of probability and stochastic analysis are given to explain ideas concerning derivative pricing and hedging. To keep the reader intrigued and motivated, the book has a ‘sandwich’ structure: probability and stochastics are given in situ where mathematics can be readily illustrated by application to finance.

The first part of the book introduces one of the main principles in finance — ‘no arbitrage pricing’. It also introduces main financial instruments such as forward and futures contracts, bonds and swaps, and options. The second part deals with pricing and hedging of European- and American-type options in the discrete-time setting. In addition, the concept of complete and incomplete markets is discussed. Elementary probability is briefly revised and discrete-time discrete-space stochastic processes used in financial modelling are considered. The third part introduces the Wiener process, Ito integrals and stochastic differential equations, but its main focus is the famous Black–Scholes formula for pricing European options. Some guidance for further study within this exciting and rapidly changing field is given in the concluding chapter. There are approximately 100 exercises interspersed throughout the book, and solutions for most problems are provided in the appendices.

Contents:

• • Historical Remarks
• Financial Instruments and Arbitrage:
  • Preliminary Examples
  • Forwards, Futures and Arbitrage
  • Bonds and Swaps
  • European Options
  • Problems for Part I
• Discrete-Time Stochastic Modelling and Option Pricing:
  • Binary Model of Price Evolution
  • Elements of Probability Theory
  • Discrete-Time Stochastic Processes
  • Multiperiod Binary Tree Model
  • Complete and Incomplete Markets
  • American Options
  • Problems for Part II
• Continuous-Time Stochastic Modelling and the Black—Scholes Formula:
  • Connection to 'Reality'
  • Probabilistic Model for an Experiment with Infinitely Many Outcomes
  • Limit of the Discrete-Price Model and Price of a European Option in the Continuous-Time Case
  • Brownian Motion (Wiener Process)
  • Simplistic Introduction to Ito Calculus
  • Problems for Part III
  • Further Study
  • Appendix: Solutions

Readership: Undergraduate and postgraduate students taking a course in financial mathematics.

Chapter 1

Historical Remarks

We begin with a sketch of the history of the subject. Compared to other areas of mathematics, this is very young. A lot of research in Financial Mathematics is continuing to be carried out and there is a large demand from financial institutions for further developments. However, the origins of Financial Mathematics are in the past.

‘Since traveling was onerous (and expensive), and eating, hunting and wenching generally did not fill the 17^th century gentleman’s day, two possibilities remained to occupy the empty hours, praying and gambling; many preferred the latter.’ (Montroll and Shloringer, 1984)

People have always gambled and gambling is usually considered to be the origin of Probability theory. During the Age of Enlightenment critical thinking was applied to gambling outcomes which were beginning to be seen as more than simply ‘God’s decision’. The starting point of Probability theory is generally regarded to be an exchange of letters between Pascal (1632–1662) and Fermat (1601–1665) on some problems concerning gambling games. The first book on Probability was written by Christian Huygens (1629–1695) in 1657 under the title About the Ratios in the Game of Dice. The first mathematical book on Probability theory in the modern sense was The Art of Making Conjectures by Jacob Bernoulli (1622–1705), which was published posthumously in 1713. It contained not only probabilities in the context of gambling games but also application of Probability theory to some problems in Economics. So, even at its birth Probability theory was married to Economics and Finance.

As with all marriages, some periods are more successful than others. A major step forward in the stochastic treatment of the price of financial assets was made in the PhD thesis of a young Frenchman named Louis Bachelier (1870–1946), Théorie de la Spéculation (Bachelier, 1900, see its English translation together with a facsimile of Bachelier’s thesis and historical commentary in Davis and Etheridge, 2006). His thesis contained many results of the theory of stochastic processes as they stand today, which were only mathematically formalised later. He was essentially the first who theoretically studied Brownian motion (Wiener process), five years before Albert Einstein (Einstein, 1905). It is reasonable to speculate that if such a thesis had appeared 50 years later then Bachelier would probably have won the Nobel Prize in Economics but the world was a different place at the start of the 20th century. At this time the world was obsessed with Physics and science in general as much as it is now with money. Everybody knew Einstein’s results on diffusion but Bachelier’s results were forgotten by economists. Henri Poincare (1854–1912), one of the greatest mathematicians of all time, was Bachelier’s PhD advisor. Bachelier’s thesis was praised by his mentor Poincare but, partially due to the existing negative perception of Economics as an application of Mathematics, Bachelier was unable to join the Paris elite and spent his career in the provincial capital of Besancon near Switzerland in Eastern France (see, e.g., Courtault et al., 2000; Jarrow and Protter, 2004). We can speculate that the reason that Bachelier was not recognised during his time is that what he did was not very interesting from an applicable point of view at the beginning of the 20th century; there was no real interest in pricing financial derivatives at that time.

In the world of mathematics Bachelier’s work was known. For instance, in the famous paper that was pivotal for further development of Probability theory, A. N. Kolmogorov credits the discoveries made by Bachelier (Kolmogorov, 1931). In the 1940s Japanese mathematician Kiyosi Ito was influenced by Bachelier’s work to create his famous Stochastic Calculus (see Footnote 8 on p. 78 of Jarrow and Protter, 2004), which we now call Ito Calculus and which is the basis of modern Stochastic Analysis and theory of stochastic differential equations (SDEs) (Ito, 1944). The Second World War was raging and this meant that it was still not the right time for Finance and Stochastics to be merged.

Bachelier’s work was rediscovered by economists in the 1950s, mainly by Paul Samuelson (see Davis and Etheridge, 2006). Samuelson, Nobel Prize winner in Economics in 1970, acknowledged the impact of Bachelier’s work on his research. By the mid 1960s Stochastic Analysis was a well-developed subject thanks to the work of distinguished mathematicians including Einstein, Markov, Wiener, Kolmogorov, Levy, Doob, Ito, Gichman, Meyer and Dynkin. Mark Davis and Alison Etheridge (2006) write:

‘...when the connection was made in the 1960s between financial economics and the stochastic analysis of the day, it was found that the latter was so perfectly tuned to the needs of the former that no goal-oriented research programme could possibly have done better.’

In 1965, Samuelson (1965) introduced geometrical Brownian motion into Finance, the model which has played a central role in the development of Financial Mathematics. It was later used by Merton (1973) and Black and Scholes (1973) to derive their famous pricing formula and it is still used in financial institutions today.

A new economic situation emerged in the 1970s due to several events that had taken place since the 1960s. They led to major structural changes and to the growth of volatility in financial markets. Some of the most important of these events were: (i) transition from the policy of fixed cross rates between currencies to rates freely floating, which led to the financial crisis of 1973; (ii) the devaluation of the dollar against gold:

1971$35   per ounce
1980$570 per ounce
1984$308 per ounce;

(iii) a decline in stock trade (the decline in the USA was deeper than during the ‘Great Depression’) and (iv) the global oil crisis provoked by OPEC (the Organization of the Petroleum Exporting Countries) (for further details see, e.g., Shiryaev, 1999). The market responded promptly to the changes in the economy and option and bond futures exchanges were opened. The first specialist exchange for trading option contracts was the Chicago Board Option Exchange (CBOE). It opened in 1973 and has been successful ever since. In 1995 the derivative market was worth $15 trillion. In 2005 it was $270 trillion, which was almost 34 times the size of the US public debt. The derivative market size reached $648 trillion by the end of 2011¹ while the global economy size was estimated at about $80 trillion².

With the growing volume of derivatives and volatility in financial markets, there was also a need to reconsider pricing methods as the old ‘rule of thumb’ and regression models became inadequate (Shiryaev, 1999). More amazing than the speed with which the market responded to the changes was the time it took for science to respond. Two landmark papers were published in 1973:

1. The Pricing of Options and Corporate Liabilities (Black and Scholes, 1973);
2. The Theory of Rational Option Pricing (Merton, 1973).

They revolutionised changed the pricing methods. Their results were immediately taken on board by option traders around the world. These papers were also, in a sense, the birth of modern Financial Mathematics which has been developed quickly and occupies a lot of researchers today. More on the history of Stochastic Analysis and its application to Financial Economics can be found in, e.g., Paul and Baschnagel (1999); Courtault et al. (2000); Jarrow and Protter (2004); Davis and Etheridge (2006) and Shiryaev (1999).

As we have discussed above, the merging of theory of Finance and Mathematics, in particular Stochastic Analysis, is the foundation for modern financial markets. However, there is also a third important element: computational power, without which it is impossible to quickly price financial products, evaluate risk of large portfolios, etc. Significant computational power available to financial institutions today is vital for effective financial management.

_________________

¹According to the Bank for International Settlements (2012, p. 1).

²According to The World Factbook by CIA (2013).

Part I

Financial Instruments and Arbitrage

This story we’ll start with a riddle,
Even Alice will struggle to answer
What would remain from a fairy tale,
After it has been told?
Where, for example, is the magic horn?
Or the good fairy, where did she go?
Eh? Oh! That’s the dilemma, my friend,
And in this is the whole point.¹

In this first part of the course we will learn about one of the main principles in Finance (and hence in Financial Mathematics) – no arbitrage pricing. We will also become familiar with main financial instruments which include forward and futures contracts, bonds and swaps, and also options. This part is not mathematical and can be easily taught at a secondary school but it requires a lot of common sense and imagination.

_________________

¹Translated from a song written by Vladimir Visotsky in 1973 for an audioplay based on Lewis Carroll’s Alice in Wonderland.

Chapter 2

Preliminary Examples

2.1Lesson 1 ‘The Expected Worth of Something is not a Good Guide to its Price’

We give two simple examples which at first glance might not seem terribly relevant to the subject; however, they are very useful (especially due to their simplicity) for understanding important concepts in Financial Mathematics introduced later in the book. In connection with these examples see also Baxter and Rennie (1996).

Example 2.1. The Bookmaker. A bookmaker is taking bets on a ‘two-horse race’, namely the FA Cup final between Liverpool and West Ham United (this example was made up before the 2006 FA Cup final). He is very clever and knowledgeable. After thoroughly studying the two teams he correctly calculates that West Ham have a 25% chance of winning while Liverpool have a 75% chance. Accordingly the odds are set at 3-1 against and 3-1 on, respectively¹. This means that if you put a £1 stake on West Ham to win and they do triumph you get 3 + 1 = 4 pounds; if Liverpool win you will lose £1. Betting £3 on Liverpool to win means you will get 1 + 3 = 4 if they do win but lose £3 if they do not.

Assume that in total £15,000 is put on West Ham to win while £30,000 is put on Liverpool². If Liverpool win, the bookmaker will make a net profit of

But if West Ham win then the profit is

45000 − (15000 + 3 × 15000) = −£15000.

That is, the bookmaker makes a loss. Hence his expected profit is

25%(−...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface
• 1. Historical Remarks
• Part I: Financial Instruments and Arbitrage
• Part II: Discrete-Time Stochastic Modelling and Option Pricing ‘
• Part III: Continuous-Time Stochastic Modelling and the Black–Scholes Formula
• Bibliography
• Index