Infinity And Truth

Chitat Chong, Qi Feng, Theodore A Slaman, W Hugh Woodin

• Publisher: WSPC
• Year: 2013
• eBook ISBN: 9789814571050
• Topic: Scienze biologiche
• Subtopic: Scienza generale

This volume is based on the talks given at the Workshop on Infinity and Truth held at the Institute for Mathematical Sciences, National University of Singapore, from 25 to 29 July 2011. The chapters cover topics in mathematical and philosophical logic that examine various aspects of the foundations of mathematics. The theme of the volume focuses on two basic foundational questions: (i) What is the nature of mathematical truth and how does one resolve questions that are formally unsolvable within the Zermelo–Fraenkel Set Theory with the Axiom of Choice, and (ii) Do the discoveries in mathematics provide evidence favoring one philosophical view over others? These issues are discussed from the vantage point of recent progress in foundational studies.

The final chapter features questions proposed by the participants of the Workshop that will drive foundational research. The wide range of topics covered here will be of interest to students, researchers and mathematicians concerned with issues in the foundations of mathematics.

Contents:

• Invited Lectures:
  • Absoluteness, Truth, and Quotients (Ilijas Farah)
  • A Multiverse Perspective on the Axiom of Constructiblity (Joel David Hamkins)
  • Hilbert, Bourbaki and the Scorning of Logic (A R D Mathias)
  • Toward Objectivity in Mathematics (Stephen G Simpson)
  • Sort Logic and Foundations of Mathematics (Jouko Väänänen)
  • Reasoning about Constructive Concepts (Nik Weaver)
  • Perfect Infinites and Finite Approximation (Boris Zilber)
• Special Session:
  • An Objective Justification for Actual Infinity? (Stephen G Simpson)
  • Oracle Questions (Theodore A Slaman and W Hugh Woodin)

Readership: Mathematicians, philosophers, scientists, graduate students, academic institutions, and research organizations interested in logic and the philosophy of mathematics. Key Features:

• All the contributors are world-renowned
• The final chapter is written by Theodore A Slaman and W Hugh Woodin, who are two of the leading logicians in the world. They are also the volume editors

ABSOLUTENESS, TRUTH, AND QUOTIENTS

Ilijas Farah

Department of Mathematics and Statistics
York University
4700 Keele Street
North York, Ontario
Canada M3J 1P3
and
Matematicki Institut, Kneza Mihaila 34
Belgrade, Serbia
[email protected]

The infinite in mathematics has two manifestations. Its occurrence in analysis has been satisfactorily formalized and demystified by the

-δ method of Bolzano, Cauchy and Weierstrass. It is of course the ‘set-theoretic infinite’ that concerns me here. Once the existence of an infinite set is accepted, the axioms of set theory imply the existence of a transfinite hierarchy of larger and larger orders of infinity. I shall review some well-known facts about the influence of these axioms of infinity to the everyday mathematical practice and point out to some, as of yet not understood, phenomena at the level of the third-order arithmetic. Technical details from both set theory and operator algebras are kept at the bare minimum. In the Appendix, I include definitions of arithmetical and analytical hierarchies in order to make this paper more accessible to non-logicians. In this paper I am taking a position intermediate between pluralism and non-pluralism (as defined by P. Koellner in the entry on large cardinals and determinacy of the Stanford Encyclopaedia of Philosophy) with an eye for applications outside of set theory.

1. Finitism, ‘Countablism’ and a Little Bit Further

Let me recall von Neumann’s definition of the cumulative hierarchy. We define sets V_α for ordinals α by recursion, so that

and V_α+1 is the power-set of V_α for every α. If δ is a limit ordinal, we let V_α =

V_α. The Power-Set Axiom asserts the existence of V_α+1, granted V_α exists. The existence of V_δ for a limit ordinal δ follows from the Replacement Axiom. We therefore have an increasing collection of sets, indexed by all ordinals, that provides framework for all of mathematics as we know it. All of number theory is formalized within V_ω. Every countable set, such as

, or the free group with two generators, has an isomorphic copy inside V_ω (where ω is the least infinite ordinal). These sets, as well as all real numbers (defined via Dedekind cuts) belong to V_ω+1. The set of real numbers therefore belongs to V_ω+2. If A is a separable metric structure, such as

₂, Tsirelson’s Banach space, or Cuntz algebra

₂, then it has a countable dense subset A₀ that can be identified (equipped with all of its metric, algebraic, and relational structure) with an element of V_ω+1. Therefore, A itself, identified with the equivalence classes of Cauchy sequences in A₀, belongs to V_ω+3. This also applies to objects that are separable in at least one natural metric, e.g., II₁ factors (

₂ metric) or multipliers of separable C*-algebras (strict metric). Quotients, coronas, ultrapowers, or double duals of separable objects, as well as their automorphism groups, all belong to V_ω+n for a relatively small natural number n. Therefore V_ω+ω already provides framework for most of non-set-theoretic mathematics.^a Nevertheless, V_ω+ω is not a model of ZFC since it fails the Replacement Axiom.

Accepting the existence of the empty set and the assertion that every set has the power-set has as a consequence the existence of V_n for all natural numbers n. However, the cardinality of V₆ is roughly 10^19,738. Current estimates take number of fundamental particles in the observable universe to be less than 10⁸⁵. While these estimates are based on our current understanding of physics and are therefore subject to change, this shows that we have no concrete model of V₆. Can we nevertheless assert that V₆ exists? Can we claim that the power-set axiom is true in the physical world? For example, consider the set X of all electrons contained in this sheet of paper at this very moment. Does the power-set of X exist? (The problem may be in the comprehension axiom, or rather the question whether X is a set?)

The fact that most physical laws are only approximately true does not diminish their usefulness in concrete applications. (As von Neumann pointed out in [54], the truth is much too complicated to allow anything but approximations.) Regardless of whether the set of all reals

(or any other infinite set) exists or not, its formal acceptance provides us with remarkable mathematical tools. Accepting the transfinite hierarchy, together with some substantial large cardinal axioms, may be comparably illuminating. Present lack of arguments pro this view is fortunately counterbalanced by the complete absence of arguments against it.

2. Independence

By Gödel’s Incompleteness Theorems, every consistent theory T that includes Peano Arithmetic and has a recursive set of axioms is incomplete. Moreover, the sentence constructed by Gödel is a

arithmetical sentence (see the Appendix). This means that it asserts that every natural number n has a certain property that can can be verified by computation. Such a sentence can be independent f...

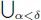
Table of contents

• Cover
• HalfTitle
• Volume
• Title
• Copyright
• Contents
• Foreword
• Preface
• Section I. Invited Lectures
• Section II. Special Session