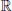Fractional Calculus: An Introduction For Physicists (2nd Edition)

An Introduction for Physicists

Richard Herrmann

• Publisher: WSPC
• Year: 2014
• ISBN:
  9789814551090
• Edition: 2
• Topic: Sciences biologiques
• Subtopic: Science générale

The book presents a concise introduction to the basic methods and strategies in fractional calculus and enables the reader to catch up with the state of the art in this field as well as to participate and contribute in the development of this exciting research area.The contents are devoted to the application of fractional calculus to physical problems. The fractional concept is applied to subjects in classical mechanics, group theory, quantum mechanics, nuclear physics, hadron spectroscopy and quantum field theory and it will surprise the reader with new intriguing insights.This new, extended edition now also covers additional chapters about image processing, folded potentials in cluster physics, infrared spectroscopy and local aspects of fractional calculus. A new feature is exercises with elaborated solutions, which significantly supports a deeper understanding of general aspects of the theory. As a result, this book should also be useful as a supporting medium for teachers and courses devoted to this subject. Contents:

• Introduction
• Functions
• The Fractional Derivative
• Friction Forces
• Fractional Calculus
• The Fractional Harmonic Oscillator
• Wave Equations and Parity
• Nonlocality and Memory Effects
• Fractional Calculus in Multidimensional Space — 2D-Image Processing
• Fractional Calculus in Multidimensional Space — 3D-Folded Potentials in Cluster Physics
• Quantum Mechanics
• The Fractional Schrödinger Equation with the Infinite Well Potential — Numerical Results using the Riesz Derivative
• Uniqueness of a Fractional Derivative — the Riesz and Regularized Liouville Derivative as Examples
• Fractional Spin — A Property of Particles Described with the Fractional Schrödinger Equation
• Factorization
• Symmetries
• The Fractional Symmetric Rigid Rotor
• q-Deformed Lie Algebras and Fractional Calculus
• Infrared Spectroscopy of Diatomic Molecules
• Fractional Spectroscopy of Hadrons
• Magic Numbers in Atomic Nuclei
• Magic Numbers in Metal Clusters
• Fractors — Fractional Tensor Calculus
• Fractional Fields
• Gauge Invariance in Fractional Field Theories
• On the Origin of Space
• Outlook

Students and researchers in physics. Key Features:

• This was the first book on the market covering the full area of a physical application of fractional calculus
• The book provides a skillful insight into a vividly growing research area and guides the reader from his first steps on an introductory level up to the current state of the art of a physical interpretation and application in different fields
• This book enables the reader to participate and contribute to the development of this exciting research area by applying these methods in his own research area too

Chapter 1

Introduction

During recent years the interest of physicists in nonlocal field theories has been steadily increasing. The main reason for this development is the expectation that the use of these field theories will lead to a much more elegant and effective way of treating problems in particle and high-energy physics as it has been possible up to now with local field theories.

Nonlocal effects may occur in space and time. For example in the time domain the extension from a local to a nonlocal description becomes manifest as a memory effect, which roughly states that the actual behaviour of a given object is not only influenced by the actual state of the system but also by events, which happened in the past.

In a first approach this could be interpreted as an ability of the object to collect or memorize previous events, an idea going back to the physics of Aristotle and perpetuated until the post-scholastic era. But this concept already irritated Descartes [Descartes (1664)] and seems obsolete since the days of Newton.

In order to allow a better understanding of nonlocal effects, we consider as a simple example the motion of a classical particle in a dilute gas. On the left side of figure 1.1 we illustrate the free field case which is characterized by the absence of any boundaries. In that case, with a given collision rate ψ(t), the dynamics of the system is determined by a local theory.

Let us now introduce some walls or boundaries, where the gas molecules bounce off.

This situation is schematically sketched on the right of figure 1.1. In that case, at the time t − τ a fixed rate of gas molecules is scattered, but in contrast to the free field case, at the time t − τ/2 they collide with the boundaries and are reflected. At the time t the dynamics of the system is then characterized by a source term which besides ψ(t) contains an additional nonlocal term proportional to ψ(t − τ). This is a simple geometric interpretation of a nonlocal theory. Neither the described particle nor the surrounding medium memorize previous events. There is no intelligence in the system. The boundaries generate a delayed reaction of the medium, which results in a memory effect.

Fig. 1.1 A possible geometric interpretation of a memory effect. The boundary free case shown on the left side is described by a local theory (characterized by a source term ψ(t)), while the same case including boundaries may be described by a nonlocal theory (characterized by a source term ψ(t) + ρψ(t − τ) with ρ being a proportionality factor).

In a more sophisticated scenario, we may assert to every point in space a complex reflection coefficient and are lead to Huygens’ principle which states that each point of an advancing wave front is in fact the source of a new set of waves.

In that sense a nonlocal theory may be interpreted as a construct which allows a smooth transition between a local (Newtonian) and a full quantum theory of motion.

A particular subgroup of nonlocal field theories plays an increasingly important role and may be described with operators of fractional nature and is specified within the framework of fractional calculus.

From a historical point of view fractional calculus may be described as an extension of the concept of a derivative operator from integer order n to arbitrary order α, where α is a real or complex value or even more complicated a complex valued function α = α(x, t):

Despite the fact that this concept is being discussed since the days of Leibniz [Leibniz (1695)] and since then has occupied the great mathematicians of their times, no other research area has resisted a direct application for centuries. Abel’s treatment of the tautochrone problem [Abel (1823)] from 1823 stood for a long time as a singular example for an application of fractional calculus.

Not until the works of Mandelbrot [Mandelbrot (1982)] on fractal geometry in the early 1980’s was the interest of physicists attracted by this subject, and a first wave of publications in the area of fractional Brownian motion and anomalous diffusion processes was created. But these works lead only to possibly a handful of useful applications and did not produce results of far-reaching consequences [Kilbas et al. (2003)].

The situation changed drastically by the progress made in the area of fractional wave equations during the last years. Within this process, new questions in fundamental physics have been raised, which cannot be formulated adequately using traditional methods. Consequently a new research area has emerged, which allows for new insights and intriguing results using new methods and approaches.

The interest in fractional wave equations was amplified in 2000 with a publication by Raspini [Raspini (2000)]. He deduced a SU(3) symmetric wave equation, which turned out to be of fractional nature. In contrast to this formal derivation a standard Yang-Mills theory is merely a recipe for coupling any phenomenologically deduced symmetry. Zavada [Zavada (2000)] has generalized Raspini’s result: he demonstrated, that a n-fold factorization of the d’Alembert operator automatically leads to fractional wave equations with an inherent SU(n) symmetry.

In 2002, Laskin [Laskin (2002)] on the basis of the Riesz definition [Riesz (1949)] of the fractional derivative presented a Schrödinger equation with fractional derivatives and gave a proof of Hermiticity and parity conservation of this equation.

In 2005, the Casimir operators and multiplets of the fractional extension of the standard rotation group SO(n) were calculated algebraically [Herrmann (2005a)]. A mass formula was derived, which successfully described the ground state masses of the charmonium spectrum. This may be interpreted as a first approach to investigate a fractional generalization of a standard Lie algebra, a first attempt to establish a fractional group theory and the first non trivial application of fractional calculus in multidimensional space.

In 2006, Goldfain [Goldfain (2006)] demonstrated, that the low level fractional dynamics [Tarasov and Zaslavsky (2006)] on a flat Minkowski metric most probably describes similar phenomena as a field theory in curved Riemann space time. In addition, he proposed a successful mechanism to quantize fractional free fields. Lim [Lim (2006a)] proposed a quantization description for free fractional fields of Klein-Gordon-type and investigated the temperature dependence of those fields.

In 2007, we [Herrmann (2007a)] applied the concept of local gauge invariance to fractional free fields and derived the exact interaction form in first order of the coupling constant. The fractional analogue of the normal Zeeman-effect was calculated and as a first application a mass formula was presented, which yields the masses of the baryon spectrum with an accuracy better than 1%. It has been demonstrated, that the concept of local gauge invariance determines the exact form of interaction, which in lowest order coincides with the derived group chain for the fractional rotation group.

Since then the investigation of the fractional rotation group alone within the framework of fractional group theory has led to a vast amount of interesting results, e.g. a theoretical foundation of magic numbers in atomic nuclei and metallic clusters.

Besides group theoretical methods, the application of fractional derivatives on multi dimensional space

^N and the increasing importance of numerical approaches are major developments within the last years [Herrmann (2012a); Herrmann (2013c)].

Furthermore, as long as the fractional derivative has been considered as the inverse of a fractional integral, which per se is nonlocal its nonlocality was a common paradigm. But recent years have seen an increasing number of alternative approaches, which are not necessarily founded on nonlocality [Samko et al.(1993b); Tarasov (2008b); Herrmann (2013b)].

Another increasing area of research is the investigation of genetic differential equations with variable order fractional derivatives based on an idea of Samko and Ross [Samko and Ross (1993a)], where the form and type of a differential operator changes with time or space respectively emphasizing evolutionary aspects of dynamic behavior.

Covering the above mentioned subjects, this book is an invitation to the interested student and to the professional researcher as well. It presents a thorough introduction to the basics of fractional calculus and routes the reader up to the current state of the art of a physical interpretation.

What makes this textbook unique is its application oriented approach. A large body of literature already covers the mathematical aspects of fractional calculus and the classical aspects of fractional calculus like anomalous diffusion and fractional Brownian motion (e.g. [Oldham and Spanier (1974); Samko et al.(1993b); Miller and Ross (1993); Kiryakova (1994); Gorenflo and Mainardi (1997); Podlubny (1999); Hilfer (2000); Hilfer (2008); Mainardi (2010); Monje et al.(2010); Klafter et al.(2011); Ortigueira (2011a); Tarasov (2011); Baleanu et al.(2012); Torres and Malinowska (2012); Uchaikin (2012); Ibe (2013); Jumarie (2014)]).

This book is explicitly devoted to the practical consequences of a use of fractional calculus in different branches of physics from classical mechanics up to quantum fields.

The book may be divided into two parts. Chapters 2 to 10 give a step by step introduction to the techniques and methods derived in fractional calculus and their application to classical problems. Chapters 11 to 26 are devoted to a concise introduction of fractional calculus in the area of quantum mechanics of multi-particle systems. The application of group theoretical methods will lead to new and unexpected results. The reader is directly lead to the actual state of research. All derived results are directly compared to experimental findings. As a consequence, the reader is guided on a solid basis and is encouraged to apply the fractional calculus approach in his research area, too.

It will be demonstrated, that the viewpoint of fractional calculus leads to new insights and surprising interrelations of classical fields of research that remain unconnected until now.

Chapter 2

Functions

What is number?

When the Pythagoreans believed that everything is number they had in mind primarily integer numbers or ratios of integers [Burkert (1972)]. The discovery of additional number types, first ascribed to Hippasus of Metapontum, at that time must have been both, a deeply shocking as well as an extre...

Table of contents

• Cover
• Halftitle
• Title Page
• Copyright Page
• Dedication
• Preface to the Second Edition
• Preface to the First Edition
• Acknowledgements
• Contents
• List of Exercises
• 1. Introduction
• 2. Functions
• 3. The Fractional Derivative
• 4. Friction Forces
• 5. Fractional Calculus
• 6. The Fractional Harmonic Oscillator
• 7. Wave Equations and Parity
• 8. Nonlocality and Memory Effects
• 9. Fractional Calculus in Multidimensional Space — 2D-Image Processing
• 10. Fractional Calculus in Multidimensional Space — 3D-Folded Potentials in Cluster Physics
• 11. Quantum Mechanics
• 12. The Fractional Schrödinger Equation with the Infinite Well Potential — Numerical Results using the Riesz Derivative
• 13. Uniqueness of a Fractional Derivative — the Riesz and Regularized Liouville Derivative as Examples
• 14. Fractional Spin — A Property of Particles Described with the Fractional Schrödinger Equation
• 15. Factorization
• 16. Symmetries
• 17. The Fractional Symmetric Rigid Rotor
• 18. q-deformed Lie Algebras and Fractional Calculus
• 19. Infrared Spectroscopy of Diatomic Molecules
• 20. Fractional Spectroscopy of Hadrons
• 21. Magic Numbers in Atomic Nuclei
• 22. Magic Numbers in Metal Clusters
• 23. Fractors — Fractional Tensor Calculus
• 24. Fractional Fields
• 25. Gauge Invariance in Fractional Field Theories
• 26. On the Origin of Space
• 27. Outlook
• Appendix A Solutions to exercises
• Bibliography
• Index