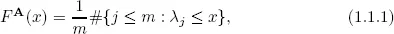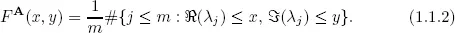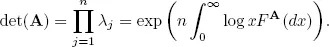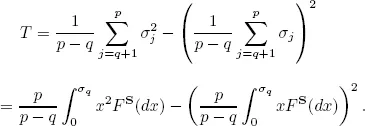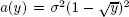Spectral Theory Of Large Dimensional Random Matrices And Its Applications To Wireless Communications And Finance Statistics: Random Matrix Theory And Its Applications

Random Matrix Theory and its Applications

Zhidong Bai, Zhaoben Fang, Ying-Chang Liang

• Publisher: WSPC
• Year: 2014
• ISBN:
  9789814579070
• Topic: Biowissenschaften
• Subtopic: Wissenschaft Allgemein

The book contains three parts: Spectral theory of large dimensional random matrices; Applications to wireless communications; and Applications to finance. In the first part, we introduce some basic theorems of spectral analysis of large dimensional random matrices that are obtained under finite moment conditions, such as the limiting spectral distributions of Wigner matrix and that of large dimensional sample covariance matrix, limits of extreme eigenvalues, and the central limit theorems for linear spectral statistics. In the second part, we introduce some basic examples of applications of random matrix theory to wireless communications and in the third part, we present some examples of Applications to statistical finance.

Contents:

• Introduction
• Limiting Spectral Distributions
• Extreme Eigenvalues
• Central Limit Theorems of Linear Spectral Statistics
• Limiting Behavior of Eigenmatrix of Sample Covariance Matrix
• Wireless Communications
• Limiting Performances of Linear and Iterative Receivers
• Application to Finance

Readership: Graduate students and researchers in random matrices.

1

---

Introduction

1.1 History of RMT and Current Development

The aim of this book is to introduce main results in the spectral theory of large dimensional random matrices (RM) and its rapidly spreading applications to many applied areas. As illustration, we briefly introduce some applications to the wireless communications and finance statistics.

In the past three or four decades, a significant and constant advancement in the world has been in the rapid development and wide application of computer science. Computing speed and storage capability have increased thousands folds. This has enabled one to collect, store and analyze data sets of huge size and very high dimension. These computational developments have had strong impact on every branch of science. For example, R. A. Fisher’s resampling theory had been silent for more than three decades due to the lack of efficient random number generators, until Efron proposed his renowned bootstrap in the late 1970’s; the minimum L₁ norm estimation had been ignored for centuries since it was proposed by Laplace, until Huber revived it and further extended it to robust estimation in the early 1970’s. It is difficult to imagine that these advanced areas in statistics would have gotten such deep stages of development if there were no such assistance from the present day computer.

Although modern computer technology helps us in so many aspects, it also brings a new and urgent task to the statisticians. All classical limiting theorems employed in statistics are derived under the assumption that the dimension of data is fixed. However, it has been found that the large dimensionality would bring intolerable error when classical limiting theorems is employed to large dimensional statistical data analysis. Then, it is natural to ask whether there are any alternative theories can be applied to deal with large dimensional data. The theory of random matrix (RMT) has been found itself a powerful tool to deal some problems of large dimensional data.

1.1.1 A brief review of RMT

RMT traces back to the development of quantum mechanics (QM) in the 1940’s and early 1950’s. In QM, the energy levels of a system are described by eigenvalues of an Hermitian operator A on a Hilbert space, called the Hamiltonian. To avoid working with an infinite dimensional operator, it is common to approximate the system by discretization, amounting to a truncation, keeping only the part of the Hilbert space that is important to the problem under consideration. Hence, the limiting behavior of large dimensional random matrices attracts special interest among those working in QM and many laws were discovered during that time. For a more detailed review on applications of RMT in QM and other related areas, the reader is referred to the Books Random Matrices by Mehta (1991, 2004) and Bai and Silverstein (2006, 2009).

In the 1950’s in an attempt to explain the complex organizational structure of heavy nuclei, E. P. Wigner, Jones Professor of Mathematical Physics at Princeton University, put forward a heuristic theory. Wigner argued that one should not try to solve the Schrödinger’s equation which governs the n strongly interacting nucleons for two reasons firstly, it is computationally prohibitive - which perhaps remains true even today with the availability of modern high speed machines and, secondly the forces between the nucleons are not very well understood. Wigner’s proposal is a pragmatic one: One should not compute from the Schrödinger’s equation the energy levels, one should instead imagine the complex nuclei as a black box described by n × n Hamiltonian matrices with elements drawn from probability distribution with only mild constraint dictated by symmetry consideration.

Along with this idea, Wigner (1955, 1958) proved that the expected spectral distribution of a large dimensional Wigner matrix tends to the famous semicircular law. This work was generalized by Arnold (1967, 1971) and Grenander (1963) in various aspects. Bai and Yin (1988a) proved that the spectral distribution of a sample covariance matrix (suitably normalized) tends to the semicircular law when the dimension is relatively smaller than the sample size. Following the work of Marčenko and Pastur (1967) and Pastur (1972, 1973), the asymptotic theory of spectral analysis of large dimensional sample covariance matrices was developed by many researchers including Bai, Yin, and Krishnaiah (1986), Grenander and Silverstein (1977), Jonsson (1982), Wachter (1978), Yin (1986), and Yin and Krishnaiah (1983). Also, Bai, Yin, and Krishnaiah (1986, 1987), Silverstein (1985a), Wachter (1980), Yin (1986), and Yin and Krishnaiah (1983) investigated the limiting spectral distribution of the multivariate F-matrix, or more generally, of products of random matrices. In the early 1980’s, major contributions on the existence of LSD and their explicit forms for certain classes of random matrices were made. In recent years, research on RMT is turning toward second order limiting theorems, such as the central limit theorem for linear spectral statistics, the limiting distributions of spectral spacings and extreme eigenvalues.

1.1.2 Spectral Analysis of Large Dimensional Random Matrices

Suppose A is an m × m matrix with eigenvalues λ_j, j = 1, 2, · · · , m. If all these eigenvalues are real, e.g., if A is Hermitian, we can define a one-dimensional distribution function

called the empirical spectral distribution (ESD) of the matrix A. Here #E denotes the cardinality of the set E. If the eigenvalues λ_j’s are not all real, we can define a two-dimensional empirical spectral distribution of the matrix A:

One of the main problems in RMT is to investigate the convergence of the sequence of empirical spectral distributions {F^A_n} for a given sequence of random matrices {A_n}. The limit distribution F (possibly defective), which is usually nonrandom, is called the Limiting Spectral Distribution (LSD) of the sequence {A_n}.

We are especially interested in sequences of random matrices with dimension (number of columns) tending to infinity, which refers to the theory of large dimensional random matrices.

The importance of ESD is due to the fact that many important statistics in multivariate analysis can be expressed as functionals of the ESD of some RM. We give now a few examples.

Example 1.1. Let A be an n × n positive definite matrix. Then

Example 1.2. Let the covariance matrix of a population have the form Σ = Σ_q + σ²I, where the dimension of Σ is p and the rank of Σ_q is q(< p). Suppose S is the sample covariance matrix based on n iid. samples drawn from the population. Denote the eigenvalues of S by σ₁ ≥ σ₂ ≥ · · · ≥ σ_p. Then the test statistic for the hypothesis H₀ : rank(Σ_q) = q against H₁ : rank(Σ_q) > q is given by

1.1.3 Limits of Extreme Eigenvalues

In applications of the asymptotic theorems of spectral analysis of large dimensional random matrices, two important problems arose after the LSD was found. The first is the bound on extreme eigenvalues; the second is the convergence rate of the ESD, with respect to sample size. For the first problem, the literature is extensive. The first success was due to Geman (1980), who proved that the largest eigenvalue of a sample covariance matrix converges almost surely to a limit under a growth condition on all the moments of the underlying distribution. Yin, Bai, and Krishnaiah (1988) proved the same result under the existence of the 4th moment, and Bai, Silverstein, and Yin (1988) proved that the existence of the 4th moment is also necessary for the existence of the limit. Bai and Yin (1988b) found the necessary and sufficient conditions for almost sure convergence of the largest eigenvalue of a Wigner matrix. By the symmetry between the largest and smallest eigenvalues of a Wigner matrix, the necessary and sufficient conditions for almost sure convergence of the smallest eigenvalue of a Wigner matrix was also found.

Comparing to almost sure convergence of the largest eigenvalue of a sample covariance matrix, a relatively harder problem is to find the limit of the smallest eigenvalue of a large dimensional sample covariance matrix. The first attempt was made in Yin, Bai, and Krishnaiah (1983), in which it was proved that the almost sure limit of the smallest eigenvalue of a Wishart matrix has a positive lower bound when the ratio of dimension to the degrees of freedom is less than 1/2. Silverstein (1984) modified the work to allowing the ratio less than 1. Silverstein (1985b) further proved that with probability one, the smallest eigenvalue of a Wishart matrix tends to the lower bound of the LSD when the ratio of dimension to the degrees of freedom is less than 1. However, Silverstein’s approach strongly relies on the normality assumption on the underlying distribution and thus, it cannot be extended to the general case. The most current contribution was made in Bai and Yin (1993) in which it is proved that under the existence of the fourth moment of the underlying distribution, the smallest eigenvalue (when p ≤ n) or the p − n + 1st smallest eigenvalue (when p > n) tends to

, where y = lim(p/n) ∈ (0, ∞). Comparing to the case of the largest eigenvalues of a sample covariance matrix, the existence of the fourth moment seems to be necessary also for the problem of the smallest eigenvalue. However,...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Preface
• Contents
• 1 Introduction
• 2 Limiting Spectral Distributions
• 3 Extreme Eigenvalues
• 4 Central Limit Theorems of Linear Spectral Statistics
• 5 Limiting Behavior of Eigenmatrix of Sample Covariance Matrix
• 6 Wireless Communications
• 7 Limiting Performances of Linear and Iterative Receivers
• 8 Application to Finance
• References
• Index