Mathematics, Poetry and Beauty

Ron Aharoni

• Publisher: WSPC
• Year: 2014
• ISBN:
  9789814602969
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

What does mathematics have to do with poetry? Seemingly, nothing. Mathematics deals with abstractions while poetry with emotions. And yet, the two share something essential: Beauty. “Euclid alone has looked on beauty bare,” says the title of a poem by Edna St. Vincent Millay.

“Mathematics, Poetry and Beauty” tries to solve the secret of the similarity between the two domains. It tries to explain how a mathematical argument and a poem can move us in the same way. Mathematical and poetic techniques are compared, with the aim of showing how they evoke the same sense of beauty.

The reader may find that, as Bertrand Russell said, “Mathematics, rightly viewed, possesses not only truth, but supreme beauty — a beauty hold and austere, like that of sculpture … sublimely pure, and capable of a stern perfection such as only the greatest art can show.”

Contents:

• The Magic of Poetry and of Mathematics
• Condensation
• Order
• How Mathematicians and Poets Think
• Poetic Image
• Mathematical Image
• Paradoxes and Oxymorons
• Self Reference and Godel's Theorem

Readership: Those interested in Mathematics, those interested in poetry, and the general public.
Key Features:

• It presents laymen and mathematicians alike with beautiful pieces of mathematics, and studies techniques of both poetry and mathematics that contribute to beauty

Part I: Order

God is a mathematician of a very high order

James Jeans, English physicist, 1877–1946

The Curious Case of the Ants on the Pole

Only about myself did I know how to speak.

My world is as narrow as that of an ant.

Rachel Bluwstein, Israeli poetess, 1890–1931

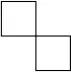
There is an unknown number of ants on a one-meter long pole. The ants move — some to the right, others to the left, but all at the same speed: exactly one meter a minute. The pole is narrow, about as wide as a single ant, and when two ants meet they cannot continue. They then behave like colliding billiard balls, that is, each turns about and continues in the opposite direction, at the same speed.

When two ants meet (left) they change direction (right).

Every so often, an ant reaches one of the pole ends, and then it falls off and disappears forever.

Question: In the end, will all the ants fall off the pole? If so, how long will this take?

At first glance, the answer seems to depend on the initial state, that is, on the number of ants on the pole and their position. If there are many ants, it seems that it might take a long time for all of them to fall off. How can we test this? I have already told you the first secret of thinking mathematically: studying examples. Mathematical thought is a play between examples and abstractions. The difference between the two is that strokes in the direction of the concrete can be done consciously, that is, examples can be evoked deliberately. For this reason one ought to begin with examples. An additional reason, of course, is that examples are the raw material of abstraction. In the case of the ants, the simplest example is that of a single ant. If the ant is at one end of the pole and goes toward the other end, it will fall off in one minute. In any other case, it will fall in less than a minute. But we still have not touched upon the core of the problem: the collisions. So let us look at two ants, located at the opposite ends of the pole, advancing toward each other.

After half a minute, they will meet in the middle of the pole, reverse their directions, and fall off in another half a minute. So, both will fall after exactly one minute.

The next example is a bit less obvious. Imagine one ant starting at the right end, the other exactly in the middle, and they are advancing toward each other.

The ants will meet after a quarter of a minute at a distance of a quarter of a meter from the right end. They will reverse their directions, and then the last ant to fall will be the ant on the left, that will fall after three quarters of a minute. After exactly one minute, both ants will have fallen.

This is starting to look strange. In all three examples, all ants fell off the pole within one minute. Let us go up one level of complexity higher, and examine three ants. Consider the case where ant A starts from the left end, and moves to the right; ant B starts from the middle and moves to the right; and ant C starts at the right end and moves to the left.

After a quarter of a minute we shall see the following picture:

After the collision, ants A and B will go towards each other, meet in the middle after another quarter of a minute, reverse their directions and each will fall after another half a minute. Ant C will had fallen from the right end even before that. Again, it will take a total of one minute for all ants to fall.

Now this is really strange. In all our examples, all the ants fell within a minute. Does this always hold true? The answer is “yes,” and the proof is easy. That is, if you have the right insight. Strange as it may seem, this insight does not add information but ignores information: it ignores the identity of the ants. If we don’t care who the ants are, then what happens at the moment two ants meet? Actually, nothing. Before their meeting, one ant goes to the left, and the other to the right; after their encounter, the exact same thing happens: then too, one ant proceeds to the left, and the other to the right, at the same speed. But for our purpose, which ant goes to the left and which goes to the right doesn’t matter.

So in effect, there are no collisions. They were only there to confuse us. The problem is completely identical to the problem: “ants are proceeding along a one meter long pole, each at the speed of one meter per minute, without colliding and without changing direction. How long will it take for them to fall?” There is no mystery here. All will fall off in one minute or less.

Mathematicians are a lucky breed. They get paid to play. When we take into account the billions that are invested in mathematical research and education, we would expect them to be busy with applied projects. In reality, most mathematician allow themselves to indulge in problems like this one. Why? Because the impractical appearance of this riddle is misleading. In fact, it is a good example of the discipline’s primary strength: abstraction. The ants in the problem are mathematical: real ants do not move at a uniform speed, and do not obey such simple rules. Mathematics is the study of systems that follow well defined rules. And the abstraction is even more evident in the solution, that strips the situation of its details, and exposes its essence.

Ignoring the irrelevant, as in the ants problem, is a primary characteristic of mathematical thought. Mathematics takes the abstraction process to its extreme. It takes a complex looking tree, strips it of its leaves, and reveals the trunk. Think, for example, of the concept of number. The person who invented the number “4” understood that, as far as the rules of arithmetic are concerned, it is immaterial if he had 4 stones or 4 pencils, what color they are, and how they are arranged. 4 stones and 3 stones are 7 stones, just as 4 pencils and 3 pencils are 7 pencils, and hence we can say abstractly “4 + 3 = 7.” Abstraction is generalization, and generalization saves effort. The rule we found for stones will be valid for any kind of objects, and at any point in time. “Mathematics is being lazy,” said the mathematician George Polya (1887–1985), “it is letting the principles do the work for you.” In this respect, the ants question is very practical. Directly, it is not useful for anything, because there are no ants like these in reality, but it educates the person who solves it to think abstractly.

It may even be the case that problem was invented to model a real-world phenomenon. Bundles of light waves (“solitons”) behave in collisions just like the ants in the solution: they pass through one another.

Hidden Order

Nature does nothing in vain, and more is vain, when less will serve;
for Nature is pleased with simplicity.

Isaac Newton

Isaac Newton, English mathematician and physicist (1642–1727). In 1666, his “miraculous year,” he fled from the plague to the village where he had been born, where in one summer he developed the theory of gravity, several of the principles of modern optics, and differential and integral calculus. He spent his later years in disputes over priorities (especially with the German Gottfried Wilhelm Leibniz, on the discovery of differential and integral calculus), in experiments in alchemy, and as master of the British royal mint.

The power of concepts

A good concept is like a path that suddenly opens before you in a dark forest. A minute ago the thicket seemed impenetrable; but from the moment the path was revealed, the way stands open. The English mathematician Andrew Wiles, who solved the famous Fermat’s Conjecture, used another metaphor. A good concept is like a light switch, that you find as you feel your way in a dark castle. When you turn on the light, you know what is in the room you are in. In the next room you will have to look for another switch.

Here is a classic example, a problem composed in 1946 by Max Black, a British philosopher and mathematician. Take an 8 × 8 board of 64 squares, and cut out the lower left-hand corner and the top right-hand corner, like this:

Can all 62 squares be covered by 31 dominoes?

You also have 31 dominoes, each of which can cover two adjacent squares of the board. All together, they can cover 62 squares, which is the number of squares on the incised board. Can the board be covered with these dominoes?

You may have guessed the first step: look at small cases, even very small. The smallest possible example is a 2 × 2 board. After the removal of two opposing squares, we get:

Of course, this shape cannot be covered with a single domino. Now try a 4 × 4 board (We are skipping the case of a 3 × 3 board, since it contains 9 squares, and removing 2 leaves 7 squares, which is an odd number. An odd number of squares cannot be covered without overlapping, since each domino covers 2 squares). A bit of experimentation will convince you that this is impossible.

In a 2 × 2 or 4 × 4 board it is easy to check all possibilities. In an 8 × 8 board this would be impractical, there are too many possibilities. We need an idea. And the concept that hits the mark is coloring the squares black and white.

Things ...

Table of contents

• Cover
• Half Title
• Title
• Copyright
• Contents
• Introduction: Magic
• Mathematics and Poetry
• Displacement
• Part I: Order
• Part II: How Mathematicians and Poets Think
• Part III: Two Levels of Perception