Combinatorial Identities For Stirling Numbers: The Unpublished Notes Of H W Gould

The Unpublished Notes of H W Gould

Jocelyn Quaintance, H W Gould

• Publisher: WSPC
• Year: 2015
• ISBN:
  9789814725293
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This book is a unique work which provides an in-depth exploration into the mathematical expertise, philosophy, and knowledge of H W Gould. It is written in a style that is accessible to the reader with basic mathematical knowledge, and yet contains material that will be of interest to the specialist in enumerative combinatorics. This book begins with exposition on the combinatorial and algebraic techniques that Professor Gould uses for proving binomial identities. These techniques are then applied to develop formulas which relate Stirling numbers of the second kind to Stirling numbers of the first kind. Professor Gould's techniques also provide connections between both types of Stirling numbers and Bernoulli numbers. Professor Gould believes his research success comes from his intuition on how to discover combinatorial identities.

This book will appeal to a wide audience and may be used either as lecture notes for a beginning graduate level combinatorics class, or as a research supplement for the specialist in enumerative combinatorics.

This book is a unique work which provides an in-depth exploration into the mathematical expertise, philosophy, and knowledge of H W Gould. It is written in a style that is accessible to the reader with basic mathematical knowledge, and yet contains material that will be of interest to the specialist in enumerative combinatorics. This book begins with exposition on the combinatorial and algebraic techniques that Professor Gould uses for proving binomial identities. These techniques are then applied to develop formulas which relate Stirling numbers of the second kind to Stirling numbers of the first kind. Professor Gould's techniques also provide connections between both types of Stirling numbers and Bernoulli numbers. Professor Gould believes his research success comes from his intuition on how to discover combinatorial identities.

This book will appeal to a wide audience and may be used either as lecture notes for a beginning graduate level combinatorics class, or as a research supplement for the specialist in enumerative combinatorics.

Readership: Undergraduates, graduates and researchers interested in combinatorial and algebraic techniques.
Key Features:

• Professor Gould is an acknowledged expert in the field of Stirling number identities
• For the first time in print, this book collects Professor's Gould's vast knowledge on this subject in one accessible location
• This book contains Professor Gould's unique approaches to discovering and proving binomial identities
• This book contains many fully-worked detailed proofs of the identities found in H W Gould's "Combinatorial Identities: A Standardized Set of Tables Listing 500 Binomial Coefficient Summations"

Chapter 1

Basic Properties of Series

The purpose of this book is to develop Professor Gould’s formulas for relating Stirling numbers of the second kind to Stirling numbers of the first kind via Bernoulli numbers. Many of these relationships rely on Professor Gould’s techniques for evaluating series whose summands are binomial coefficients. Therefore, the first eight chapters of this book will be a primer on these various techniques. Assume n and k are nonnegative integers with k ≤ n. Define n! to be the product of the first n positive integers and

with 0! := 1. Combinatorially

counts the number of subsets of size k made from a set with n elements. We say

is a binomial coefficient. The binomial coefficients are often displayed in Pascal’s triangle. Pascal’s triangle begins with

, and for row i, with i ≥ 2, the j^th entry from the left is

. Each row of the Pascal’s triangle contains only a finite number of entries since

whenever k > n.

Table 1.1: A portion of Pascal’s triangle

There is an inductive way to construct the rows of Pascal’s triangle which is known as Pascal’s identity.

Pascal’s Identity: Let n and k be nonnegative integers, with 0 ≤ k ≤ n. Define

if k is a negative integer. Then

Here is a combinatorial proof of Pascal’s identity. In this and other combinatorial arguments we show both sides of a given equation count the same quantity. Suppose S = {1, 2, 3, …, n + 1}. The left side of Equation (1.1) counts the number of subsets of S with size k. Call such a subset a k-subset of S. We claim the right side of Equation (1.1) also counts the k-subsets of S. There are two distinct types of k-subsets. The first type of k-subset contains n + 1. To complete such a subset, we must choose k − 1 elements from {1, 2, …, n} in

possible ways. The second type of k-subset does not contain n + 1, and we must select k elements from {1, 2, …, n} in

possible. Adding the two possibilities together counts all the k-subsets of S without repetition and produces Equation (1.1).

Mathematicians often generalize definitions, and the binomial coefficients are no exceptions. The typical way to generalize

is to let n be an arbitrary complex number. We will always assume, unless otherwise specified, that k is a nonnegative integer, and x is a complex number. Define

and

We say

is a general binomial coefficient. Whenever x = n, Equation (1.2) corresponds to the traditional combinatorial definition of a binomial coefficient.

It is important to note that

is a polynomial in x of degree k. This observation, along the with Fundament...

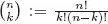
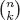
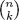
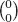
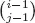
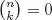
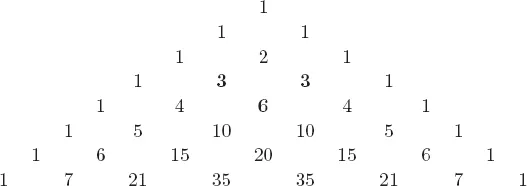
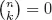
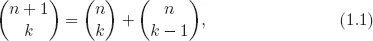
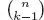
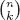
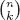
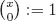
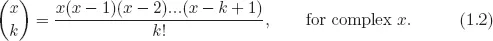
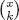
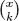
Table of contents

• Cover Page
• Title Page
• Copyright
• Dedication
• Foreword
• Preface
• Acknowledgments
• Contents
• 1. Basic Properties of Series
• 2. The Binomial Theorem
• 3. Iterative Series
• 4. Two of Professor Gould’s Favorite Algebraic Techniques
• 5. Vandermonde Convolution
• 6. The nth Difference Operator and Euler’s Finite Difference Theorem
• 7. Melzak’s Formula
• 8. Generalized Derivative Formulas
• 9. Stirling Numbers of the Second Kind S(n, k)
• 10. Eulerian Numbers
• 11. Worpitzky Numbers
• 12. Stirling Numbers of the First Kind s(n, k)
• 13. Explicit Formulas for s(n, n − k)
• 14. Number Theoretic Definitions of Stirling Numbers
• 15. Bernoulli Numbers
• Appendix A Newton-Gregory Expansions
• Appendix B Generalized Bernoulli and Euler Polynomials
• Bibliography
• Index