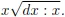Fractional Quantum Mechanics

Nick Laskin

• Publisher: WSPC
• Year: 2018
• ISBN:
  9789813223813
• Topic: Sciences physiques
• Subtopic: Théorie des quanta

-->

Fractional quantum mechanics is a recently emerged and rapidly developing field of quantum physics.

This is the first monograph on fundamentals and physical applications of fractional quantum mechanics, written by its founder.

The fractional Schrödinger equation and the fractional path integral are new fundamental physical concepts introduced and elaborated in the book. The fractional Schrödinger equation is a manifestation of fractional quantum mechanics. The fractional path integral is a new mathematical tool based on integration over Lévy flights. The fractional path integral method enhances the well-known Feynman path integral framework.

Related topics covered in the text include time fractional quantum mechanics, fractional statistical mechanics, fractional classical mechanics and the α-stable Lévy random process.

The book is well-suited for theorists, pure and applied mathematicians, solid-state physicists, chemists, and others working with the Schrödinger equation, the path integral technique and applications of fractional calculus in various research areas. It is useful to skilled researchers as well as to graduate students looking for new ideas and advanced approaches.

--> Contents:

• Preface
• What is Fractional Quantum Mechanics?
• Fractals
• Fractional Schrödinger Equation
• Time-Independent Fractional Schrödinger Equation
• Fractional Uncertainty Relation
• Path Integral Over Lévy Flights
• A Free Particle Quantum Kernel
• Transforms of a Free Particle Kernel
• Fractional Oscillator
• Some Analytically Solvable Models of Fractional Quantum Mechanics
• Fractional Nonlinear Quantum Dynamics
• Time Fractional Quantum Mechanics
• Applications of Time Fractional Quantum Mechanics
• Fractional Statistical Mechanics
• Fractional Classical Mechanics
• Fractional Dynamics in Polar Coordinate System
• Afterword
• Appendices:
  • Fox H -Function
  • Fractional Calculus
  • Calculation of the Integral
  • Polylogarithm
  • Fractional Generalization of Trigonometric Functions cos z and sin z
• Bibliography
• Index

-->
--> Readership: Graduate students and researches in quantum theory, stochastic processes, statistical mechanics, special functions. -->
Fractional Quantum Mechanics;Fractional Schrödinger Equation;Non-Linear Fractional Schrödinger Equation;Quantum Riesz Fractional Derivative;Path Integral Approach;Lévy Path Integral;Quantum Kernel;Fractional Statistical Mechanics;Time Fractional Quantum Mechanics0 Key Features:

• This is the first monograph on fractional quantum mechanics — a recently emerged and fast growing field of quantum theory
• It extends applications of fractional calculus to quantum theory
• It has been written by the founder of fractional quantum mechanics
• It presents recently developed fundamentals on the fractional Schrödinger equation and fractional path integral, and their applications to quantum mechanics and quantum statistical mechanics
• A new theoretical physics tool — the fractional path integral, presented for the first time by the book, significantly enhances the well-known Feynman's path integral approach to quantum mechanics and statistical physics
• Never before used in quantum mechanics, the Fox H-function and the Mittag-Leffler function have been introduced and used to obtain close form solutions of fractional quantum mechanical problems

Chapter 1

What is Fractional Quantum Mechanics?

1.1 Path integral

Non-relativistic quantum mechanics can be formulated in the frameworks of three different approaches: the Heisenberg matrix algebra [1]-[3] the Schrödinger equation [4]-[6] and the Feynman path integral [7]-[9]. These three, apparently dissimilar approaches, are mathematically equivalent.

The discovery of the quantum mechanical path integral approach was originated in the early ’30s by the attempt of Dirac [10] to find a relationship between classical and quantum mechanics in terms of the classical mechanics ‘least-action’ principle. In essence, Dirac searched for the role that classical mechanics fundamentals like the Lagrangian and the ‘least-action’ principle play in quantum mechanics. While he considered the Lagrangian approach to classical mechanics more fundamental than the Hamiltonian one, at the time it seemed to have no important role in quantum mechanics. Dirac speculated on how this situation might be rectified, and concluded that the propagator in quantum mechanics is “analogous” to exp(iS/ħ), where S is the classical mechanical action and ħ is Planck’s constant.

Based on Dirac’s findings Feynman developed the “integral over all paths”, the path integral. How it came to him was well described by Feynman in his Nobel lecture [11]. I went to a beer party in the Nassau Tavern in Princeton. There was a gentleman, newly arrived from Europe (Herbert Jehle) who came and sat next to me. Europeans are much more serious than we are in America because they think a good place to discuss intellectual matters is a beer party. So he sat by me and asked, “What are you doing” and so on, and I said, “I’m drinking beer.” Then I realized that he wanted to know what work I was doing and I told him I was struggling with this problem, and I simply turned to him and said “Listen, do you know any way of doing quantum mechanics starting with action – where the action integral comes into the quantum mechanics?” “No,” he said, “but Dirac has a paper in which the Lagrangian, at least, comes into quantum mechanics. I will show it to you tomorrow.” Next day we went to the Princeton Library (they have little rooms on the side to discuss things) and he showed me this paper. Dirac’s paper [10] claimed that a mathematical tool which governs the time development of a quantal system was “analogous”to the classical Lagrangian.

Professor Jehle showed me this; I read it; he explained it to me, and I said, “What does he mean, they are analogous; what does that mean, analogous? What is the use of that?” He said, “You Americans! You always want to find a use for everything!” I said that I thought that Dirac must mean that they were equal. “No,” he explained, “he doesn’t mean they are equal.” “Well,” I said, “let’s see what happens if we make them equal.” So, I simply put them equal, taking the simplest example, but soon found that I had to put a constant of proportionality A in, suitably adjusted. When I substituted and just calculated things out by Taylor-series expansion, out came the Schrödinger equation. So I turned to Professor Jehle, not really understanding, and said, “Well you see Professor Dirac meant that they were proportional.” Professor Jehle’s eyes were bugging out – he had taken out a little notebook and was rapidly copying it down from the blackboard and said, “No, no, this is an important discovery.”

Feynman’s path integral approach to quantum mechanics [12] brings deep insights into the relationship between quantum and classical mechanics and became a new efficient mathematical tool in quantum theory and mathematical physics. Feynman’s thesis advisor, J. A. Wheeler wrote in Physics Today 42, 24 (1989), “Feynman has found a beautiful picture to understand the probability amplitude for a dynamical system to go from one specified configuration at one time to another specified configuration at a later time. He treats on a footing of absolute equality every conceivable history that leads from the initial state to the final one, no matter how crazy the motion in between. The contributions of these histories differ not at all in amplitude, only in phase. And the phase is nothing but the classical action integral, apart from the Dirac factor, ħ. This prescription reproduces all of standard quantum theory. How could one ever want a simpler way to see what quantum theory is all about!”

The path integral approach due to its new overall space-time perspective gives an intuitive way of viewing quantum dynamics and understanding the classical limit of quantum mechanics.

Today Feynman’s path integrals are widely used in quantum gauge field theory and the theory of nonperturbative phenomena [13]-[17], physics of dense strongly interacting matter (quark-gluon plasma) [18], statistical physics [19], physics of polymers, theory of phase transitions and critical phenomena [20], atomic physics and high-energy radiation phenomena, quantum optics [21], [22], theory of stochastic processes and its numerous applications [23]-[26], option pricing and modeling of financial markets [20].

1.2 Fractals and fractional calculus

The Feynman path integral is in fact the integration over Brownian-like quantum paths. The Brownian path is an example of a fractal. Following Mandelbrot [27], it is said that a fractal is a self-similar object, that is the whole object looks like any of its parts (for instance, see [27], [28]). The wording “when the sum of independent identically distributed random quantities has the same probability distribution as each random quantity distributed” can be considered as an expression of self-similarity - “when does the whole object look like any of its parts”. The trajectories of Brownian motion and Lévy flight are self-similar curves. In other words, the trajectories of Brownian motion and Lévy flight can be considered as random fractals. The fractal dimension of a Lévy flight trajectory can be expressed in terms of the Lévy index α which serves as a measure of self-similarity. In fact, the Lévy index α is equal to the Hausdorff–Besicovitch dimension of trajectory of random motion [29]. That is, the fractal dimension of a trajectory of Brownian motion is 2, while the fractal dimension of a Lévy flight path is α, 0 < α ≤ 2.

If Brownian diffusion is described by the well-known diffusion equation with scaling x(t) ∼ t^1/2, then the diffusion governed by the Lévy flight process is described by a fractional diffusion equation with scaling x(t) ∼ t^1/α, 0 < α ≤ 2. The fractional diffusion equation is a well-suited mathematical model to study anomalous diffusion displaying the scaling x(t) ∼ t^1/α.

The standard diffusion equation includes a second-order spatial derivative. The fractional diffusion equation includes a fractional α-order spatial derivative. Thus, the appropriate mathematical tool to study diffusion and diffusion-like processes with 1/α scaling is a fractional diffusion equation, which belongs to the mathematical field called fractional calculus [30]-[32].

Fractional calculus is concerned with the generalization of differentiation and integration to non-integer (fractional) orders. The subject has a long history. In a letter to L’Hospital in 1695, Leibniz [33] raised the following question: “Can the meaning of derivatives with integer order be generalized to derivatives with non-integer orders?” L’Hospital was somewhat curious about the question and replied to Leibniz: “What if the order will be 1/2?” From this question, the study of fractional calculus was born. In a letter dated September 30, 1695 [33], [34] Leibniz responded to the question, “ d^1/2x will be equal to

This is an apparent paradox from which, one day, useful consequences will be drawn.” Over the centuries many brilliant mathematicians, among them Liouville, Riemann, Weyl, Fourier, Abel, Lacroix, Leibniz, Grunwald, Letnikov and Riesz, have built up a large body of mathematical knowledge on fractional integrals and derivatives. Although fractional calculus is a natural generalization of calculus, and although its mathematical history is equally long, it has just recently become the attractive efficient tool in physics and mathematics.

The important fields of application of fractional calculus in physics are the phenomena of anomalous diffusion, fractional quantum mechanics, quantum and classical dynamics with long-range interactions, long memory relaxation processes with non-exponential time decay, long tail phenomena observed in network communication systems and in the behavior of financial markets. Fractional calculus is an efficient tool to study chaotic dynamic systems and their transport properties. In particular, it helps to obtain some quantitative and qualitative results based on the known features of fractional derivatives.

In mathematics, considerable attention has been recently focused on the study of problems involving fractional spaces and nonlocal equations, where nonlocality is treated in terms of pseudo-differential operators - fractional differential operators, for example, the fractional Laplace operator. Fractional differential operators and the fractional Sobolev spaces attract the attention of many researchers, both from a pure mathematical stand point and from a stand point of various applications, since these operators naturally arise in many different contexts, such as, anomalous diffusion, fractional kinetics, fractional quantum mechanics, fractional statistical mechanics, financial mathematics, signal processing and network communication systems, theory of equilibrium and non-equilibrium phenomena in the systems with long-range interaction, theory and applications of fractional stochastic processes, etc. The bibliography on the topic is so extensive that it is a real challenge to come up with a reasonable list of references. Instead, we direct the readers to papers [31], [32], [35], [36] where an introduction to the subject and an extensive bibliography can be found.

A review of recent developments in the field of fractional calculus and its applications has been presented in [31], [32].

Among the many monographs and textbooks on fractional calculus fundamentals and their wide range of applications, books [30], [37]-[43], which target the application of fractional calculus to a variety of important natural science problems.

1.3 Lévy flights

The understanding of quantum and classical physics phenomena governed by long-range space processes has required the implementation of the Lévy flights random process [44]. It is well known that displacement of a particle from some initial point follows the well-known square root law, x(t) ∼ t^1/2. The square root law is an attribute of the well-known Brownian motion model for diffusion. However, for complex quantum and classical physics phenomena this temporal diffusive behavior has not been observed. Instead, the more general diffusion law x(t) ∼ t^1/α with 0 < α ≤ 2, where α is the Lévy index, has been found. The mathematical model to describe 1/α scaling is known as Lévy flights. What is the reason for the term “Lévy flig...

Table of contents

• Cover page
• Title page
• Copyright
• Preface
• 1. What is Fractional Quantum Mechanics?
• 2. Fractals
• 3. Fractional Schrödinger Equation
• 4. Time-Independent Fractional Schrödinger Equation
• 5. Fractional Uncertainty Relation
• 6. Path Integral over Lévy Flights
• 7. A Free Particle Quantum Kernel
• 8. Transforms of a Free Particle Kernel
• 9. Fractional Oscillator
• 10. Some Analytically Solvable Models of Fractional Quantum Mechanics
• 11. Fractional Nonlinear Quantum Dynamics
• 12. Time Fractional Quantum Mechanics
• 13. Applications of Time Fractional Quantum Mechanics
• 14. Fractional Statistical Mechanics
• 15. Fractional Classical Mechanics
• 16. Fractional Dynamics in Polar Coordinate System
• Afterword
• Appendix A Fox H-function
• Appendix B Fractional Calculus
• Appendix C Calculation of the Integral
• Appendix D Polylogarithm
• Appendix E Fractional Generalization of Trigonometric Functions cos z and sin z
• Bibliography
• Index