Philosophy of Mathematics

Thomas Bedürftig, Roman Murawski

• Publisher: De Gruyter
• Year: 2018
• ISBN:
  9783110470772
• Edition: 1
• Topic: Mathematics
• Subtopic: History & Philosophy of Mathematics
• Index: Mathematics

The present book is an introduction to the philosophy of mathematics. It asks philosophical questions concerning fundamental concepts, constructions and methods - this is done from the standpoint of mathematical research and teaching. It looks for answers both in mathematics and in the philosophy of mathematics from their beginnings till today. The reference point of the considerations is the introducing of the reals in the 19th century that marked an epochal turn in the foundations of mathematics.

In the book problems connected with the concept of a number, with the infinity, the continuum and the infinitely small, with the applicability of mathematics as well as with sets, logic, provability and truth and with the axiomatic approach to mathematics are considered. In Chapter 6 the meaning of infinitesimals to mathematics and to the elements of analysis is presented.

The authors of the present book are mathematicians. Their aim is to introduce mathematicians and teachers of mathematics as well as students into the philosophy of mathematics. The book is suitable also for professional philosophers as well as for students of philosophy, just because it approaches philosophy from the side of mathematics. The knowledge of mathematics needed to understand the text is elementary.

• 
  
  

• Reports on historical conceptions.
• Thinking about today's mathematical doing and thinking.
• Recent developments.
• Based on the third, revised German edition.
• For mathematicians - students, teachers, researchers and lecturers - and readersinterested in mathematics and philosophy.

• 
  
  

Contents
On the way to the reals
On the history of the philosophy of mathematics
On fundamental questions of the philosophy of mathematics
Sets and set theories
Axiomatic approach and logic
Thinking and calculating infinitesimally – First nonstandard steps
Retrospection

1On the way to the reals

Between the intuitional idea and the mathematical formulation which should describe the scientifically substantial elements of our intuition in precise terms, there will always remain a gap.3

Richard Courant

In this chapter we will try to trace the mathematical base of the reals and to present briefly their setting and mathematical foundations, in order to formulate problems of a philosophical, methodological and mathematical nature. We state, once again, as already indicated in the Introduction, the ignorance of those problems as well as the pragmatism in putting reals as the universal base of mathematics. One pragmatically carries on doing mathematics. The reals seem to be always there. They became quasi “natural” numbers for mathematicians. In this chapter, first of all, we want to call attention to questions lying in the background of the reals by observing carefully the way they are introduced and indicating details and problems appearing there. For the sake of clarity we choose a short and pointed formulation of the problems.

The way to the real numbers ℝ begins – as almost everything in mathematics does – with (genuine) natural numbers ℕ. We choose in this chapter a subsequent starting point: the rational numbers ℚ. It is the starting point of someone learning mathematics who does not know anything about the reals. So we put ourselves consciously in the position of a student learning mathematics – it is similar to a position of the Pythagoreans 2500 years ago. All we have and know are rational numbers and nothing else. It is a requirement in this chapter to abandon really completely all our previous knowledge. About the way from natural to rational numbers we write briefly in Chapter 3.

1.1Irrationality

What is irrationality? Consider the standard example. One looks for a number whose square is 2. It is called √2. The following result is stated everywhere.

Theorem. √2 is irrational.

A standard indirect proof of this is then given. For completeness we also shall give a proof here, and we do this by the oldest way of arguing, which one finds in Elements by Euclid [109, Book X, Section 115a].

Proof. Suppose that $\sqrt{2}$

is rational, say $\sqrt{2}=\frac{m}{n}$

, where m and n have no common divisor (i.e., they are relatively prime). Hence $2=\frac{m^2}{n^2}$

and 2 ⋅ n2 = m2. So m2 and consequently also m are even, e.g., m = 2 ⋅ a. So n should be odd because by assumption m and n have no common divisor. On the other hand since 4 ⋅ a2 = m2 = 2 ⋅ n2, one gets n2 = 2 ⋅ a2, so n2 is even, and hence n is also even. But this is a contradiction!

What does this theorem actually say? The suggestion, made even to experts, is:

is a number of another type, just an irrational number.

So what is our situation? There is nothing other than rational numbers. Hence “irrational” can mean only

$\sqrt{2}$

is not rational.

But “not rational” simply means, in the absence of other numbers, the following result.

Theorem. $\sqrt{2}$

is not a number.

This means that there is no number whose square is 2. So what is $\sqrt{2}?$

$\sqrt{2}$

is a term without any meaning.

One can however write this term to dramatize the question how it can have a sense. But at first it has no sense. So one tries to give $\sqrt{2}$

a different sense. Can it not be seen in the next standard example?

We argue thus: from the theorem of Pythagoras it follows that the square with the side being a diagonal of the unit square has a surface area equal to 2, hence the diagonal d has length $\sqrt{2}.$

If we put d on the number line then $\sqrt{2}$

can be seen there as the length of d:

This is the next suggestion which misleads an insider and lecturer and seduces a learner to accept

as a number without further ado.

What error have we committed? We naively assume that every point on a line on which we have visualized rational numbers as points represents a number. For numbers lie there densely. But what numbers do we have? Rational numbers! And just to such numbers belongs a point on a number line. Since $\sqrt{2}$

is not rational, we have found no num...

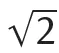
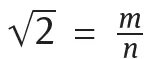
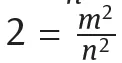
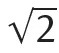
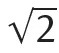
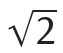
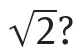
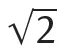
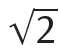
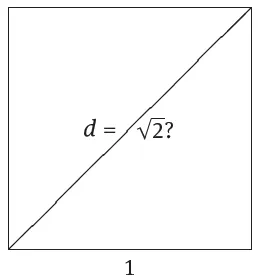
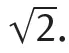
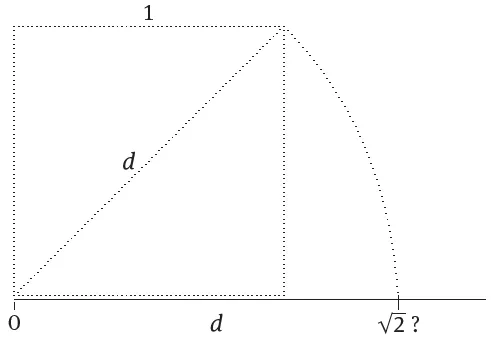
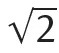
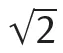
Table of contents

• Cover
• Title Page
• Copyright
• Contents
• Preface
• Introduction
• 1 On the way to the reals
• 2 On the history of the philosophy of mathematics
• 3 On fundamental questions of the philosophy of mathematics
• 4 Sets and set theories
• 5 Axiomatic approach and logic
• 6 Thinking and calculating infinitesimally – First nonstandard steps
• 7 Retrospection
• Biographies
• Bibliography
• Index of names
• Index of symbols
• Index of subjects