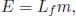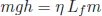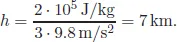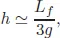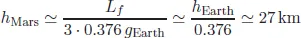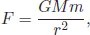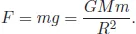Alpine Physics

Science in the Mountain Environment

Valerio Faraoni

• Publisher: WSPC
• Year: 2019
• ISBN:
  9789813274228
• Topic: Biological Sciences
• Subtopic: Environmental Science
• Index: Biological Sciences

This unique volume applies physics and basic science to the mountain environment and is written in a non-technical language for curious laypeople who wonder why or how natural phenomena happen, and what their scientific explanation may be. The book discusses physics in a non-specialized way. Alpine Physics is mostly organized in categories relevant for non-scientists with an interest in alpine environments.

Intuitive decision-making is often just grounded in plain common sense, to which mountain and nature lovers relate easily, especially when involving high-stakes decisions based on the estimation of such a treacherous environment. The book highlights how this intuitive decision-making can be complemented and augmented by basic scientific knowledge, and with better understanding it leads one to become a rational decision-maker.

The book stimulates its readers to reason and discover why things are the way they are, at high altitudes, where many risk factors are aggravated, often dramatically, by steep gradients. The writing style marries that of the conventional science textbook and that of the informal North-American climbing guidebooks.

Contents:

• Mountains High or Low, Hard or Soft:
  • Introduction
  • How High Can a Mountain Be?
  • Out of This World
  • Fallen from the Sky
  • All the Peaks, Passes, and Valleys of this Planet
  • The Rock Cycle
  • Destroying Mountains
  • Of Sweat, Rock, and Hard Places
  • Volcanoes
• Gravity Rules:
  • Introduction
  • How Hard Will a Falling Rock Hit?
  • Talus Cones, Avalanches, and Antlions: The Angle of Repose
  • Water Erosion
  • Sequoias and Capillarity
• Water, Snow, and Ice:
  • Introduction
  • Water is Unusual
  • Skis, Snowshoes, and Pressure
  • Under Stress
  • Phase Changes
  • Phase Changes at Work: Falling Rocks
  • Of Steam and Water Bottles
  • Snowflakes and Snowpack: The Whole is More than the Sum of Its Parts
  • Avalanche!
  • Suncups and Penitentes
• Glacier Puzzles:
  • Introduction
  • How Thick Can an Alpine Glacier Be?
  • How Thick Can a Polar Glacier Be?
  • How Deep Can a Crevasse Be?
  • How Long Does It Take for Snow to Turn into Ice?
  • How Did Glacial Valleys Get Their U-Shape?
  • The Universe in a Glacial Valley
• Heat, Cold, and Air:
  • Introduction
  • Why is It Cold Up There?
  • The Dress Code
  • Conserving Heat
  • Föhn, Chinook, and Bicycle Pumps
  • Valley Breeze and Mountain Breeze
  • Clear Nights are Cold Nights
  • Archimedes in the Tent
  • Air Moisture
  • Weather Forecasts
• Rock Climbing:
  • Introduction
  • Biomechanics
  • Fall Factor
  • Never Rappel from a Tight Sling
  • Beware of the American Triangle
  • The Yin and Yang of Friction
• Miscellaneous:
  • Introduction
  • Why is the Sky Blue?
  • Put Your Sunscreen On
  • Lichen It or Not
  • Places with a Lot of Potential
  • Science Labs in the Mountains
• Epilogue
• Appendix A:
  • Physical Constants
  • Differential Operators
• Appendix B
• Appendix C
• Appendix D
• Bibliography
• Index

Readership: Physics libraries; alpine clubs; outdoors clubs; mountaineering/alpine societies and organizations; environmental science programs, integrated science programs, and outdoor leadership programs in educational institutions. General Physics;Alpine Environments;Mountains;Applied Physics;Alpine Physics0 Key Features:

• Currently, the book has no competitors on the market
• The book allows readers with a passion for the mountains, for alpine environments, or for the outdoors in general to understand basic natural processes whose occurrence is enhanced, or even dramatic, in the mountains
• The treatment of the material is unique, in that the book is written from a very practical and non-academic point of view. Real life outdoors stories, followed by scientific reasoning, make the presentation of the scientific content more vivid and appealing

Chapter 1

Mountains high or low, hard or soft

1.1Introduction

Fortunately there are mountains, plenty in some geographical areas and none in others. Mountains come in various shapes, big and small, in ranges or as isolated volcanoes sticking out of the plains; mountains old or young, glaciated or rocky, and their walls, peaks, and ridges can be made of igneous, sedimentary, or metamorphic rocks which determine the slopes and the shape of the landscape. Mountains host glaciers and permanent snowfields, wide U-shaped valleys carved by glaciers, and narrow gorges through which impetuous streams run (Figs. 1.1 and 1.2).

These features give rise to a variety of physical phenomena, some of which are going to be discussed. Perhaps the most basic characteristics of mountains are hiding in plain sight and are easily missed, for example the simple statistics that no mountain on Earth is taller than about nine kilometers, or that there is a limiting thickness not only for alpine glaciers but also for the huge polar glaciers which are a few kilometers thick. There are physical reasons why things are like that. Geological forces are active building mountains and other forces destroy them simultaneously, but they can ultimately be reduced to thermal processes inside the Earth or to mechanical processes dominated by gravity on the outside. Basic concepts of physics explain features of these mountains and mathematics has something to say about them. Let us look at some of these concepts applied to the mountain environment.

Fig. 1.1 The Miage torrent rages through the V-shaped Gorge de la Gruvaz (Val Montjoie, Saint Gervais les Bains, France).

1.2How high can a mountain be?

How high can a mountain be? The summit of the highest mountain on Earth, the legendary Mt. Everest, stands 8848 meters above sea level. If one measures the elevation starting from the bottom of the ocean, Mauna Kea (4,207 meters above sea level and over 10,000 meters from the floor of the Pacific Ocean) is definitely taller than Mount Everest. Mountains are not arbitrarily high and 10 km is still a very small fraction of the radius of this planet (which is approximately 6370 km) so, relatively speaking, mountains are very small warts on the surface of our planet. In comparison, the corrugations on the peel of an orange are larger. What limits the height of a mountain? Clearly, it must be physics together with the basic properties of the materials that mountains are made of.

Fig. 1.2 Canyoning in a limestone gorge carved by running water (Val Clusa, Italy).

Most geography and geology textbooks give the answer: the maximum height of a mountain on Earth (approximately 10 km) is set by the basic physical fact that an hypothetical mountain higher than this limit would begin to melt at its base, which would flow away, hence mountains higher than about 10 km cannot exist. It is interesting that the same geography textbooks never seem to calculate this 10 km limit, nor do they provide references to support the argument (the nice picture of a mountain that is often included at this point does not do much, in terms of logic, to support or illustrate this physical argument). The calculation is really quite simple and, to the best of our knowledge, the argument was proposed by Victor Weisskopf in the 1970s [Weisskopf (1975)]. Weisskopf (1908–2002) was an Austrian-born, American-naturalized theoretical physicist who worked on building the theory of quantum mechanics with the likes of Werner Heisenberg, Erwin Schr¨odinger, Wolfgang Pauli, and Niels Bohr and later took up a leading role in the Manhattan project (after World War II, however, he campaigned against nuclear proliferation). True to his Austrian background, Weisskopf must have liked the subject of the maximum height of mountains because he discussed it again eleven years later in the famous pedagogical journal American Journal of Physics¹ [Weisskopf (1986a)] (a brief debate also ensued [Landis (1986); Weisskopf (1986b)]) and there are records of a lecture on this subject given by Weisskopf at CERN, the European organization for research in particle physics located in Geneva [CERN (2017)].

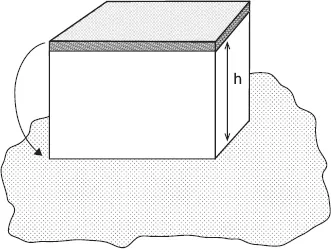
Weisskopf’s argument goes like this²: consider a horizontal parallelepiped (a very crude “mountain”) made of a most common mineral, say SiO₂, and think of making this parallelepiped thicker and thicker. This “mountain” reaches its maximum height when a layer of the same material added to its top causes plastic flow at the bottom. Weisskopf’s trick to calculate the effect and simplify the problem consists of noting that this process amounts to melting a layer of equal thickness at the base of the “mountain” (Fig. 1.3).

One does not need to actually lower this layer from the top to the bottom: we can just consider that a layer added at the top causes a layer of the same thickness to melt at the bottom and we can imagine to move the top layer to the bottom. In fact, it is sufficient to provide only a fraction η of the energy needed to melt this layer, and it is provided by the loss of gravitational potential energy (the energy that a mass has just by virtue of being up high in the presence of gravity). Weisskopf guessed the value of this factor as η ∼ 1/3. So, we equate the gravitational energy lost by lowering the top layer to the base of the “mountain” with one third of the thermal energy necessary to melt a layer of the same thickness. The latter is well known from everyday experience: as is intuitive, to melt a mass m of a material one needs to provide an energy proportional to this mass

Fig. 1.3 Weisskopf’s argument.

where L_f is a constant characteristic of the material and called latent heat of fusion.³ In a student lab the melting energy E is supplied as heat, but here it is provided by the gravitational energy which the layer of material had by virtue of being at the top of the mountain.⁴ The gravitational potential energy of a mass m at level h with respect to a reference level (in this case the bottom of the mountain) is mgh, where g = 9.8 m/s² is the acceleration of gravity. We have then

and, solving for h,

The mass m cancels out and disappears from our result, which is good, otherwise we would obtain different numbers for every different layer that we could want to consider, and all those layers would have different masses. The latent heat of fusion of SiO₂ is tabulated as L_f = 2 · 10⁵ J/kg [Clauser (2011)], which gives

To build our hypothetical “mountain”, we have used SiO₂ but we could have used instead basalt or granite, which are two other common rocks. In this case the latent heat of fusion is L_f = 4.2 · 10⁵ J/kg [Clauser (2011)], which would provide the maximum height of approximately 14 km. The calculation presented is what physicists call an order of magnitude estimate. It is not meant to be a precise calculation, which would require a lot more knowledge of physics, detailed modelling, and more mathematical sophistication, but provides only an answer correct within a factor of a few with little effort. Weisskopf’s argument identifies the key physical elements of the problem (the strength of the atomic/molecular bonds within the material, which determines the latent heat of fusion, and gravity) and does the job for us.

1.3Out of this world

We have just seen that the maximum height of a mountain made of a material with latent heat of fusion L_f is

where g is the surface gravity of the planet. Although we will never get there for a weekend trip or even for an extended climbing expedition, it is inspiring to think of mountains on other planets where the acceleration of gravity g is different from 9.8 m/s², the average value on Earth.⁵ We refer here to rocky planets like the Earth, for it would not make sense to speak of mountains on a gaseous planet like the gas giants of our Solar System Jupiter and Saturn. Take for example Mars, which has a surface gravity g equal to 0.376 g_Earth. By replacing g in our previous equation, we obtain

using h_Earth ≃ 10 km. Because gravity is weaker than on Earth, mountains on Mars can be taller than their terrestrial cousins. For example the tallest mountain on Mars, Olympus Mons, a shield volcano, is approximately 22 km high.

The maximum height of a mountain on a planet is related to another topic which interests astrophysicists. Thinking about it, it is easy to compute the surface gravity of a planet using Newton’s theory of gravity if we know its mass M and its radius R (what is not easy is to measure the mass and the radius of distant planets, but that has been done with many years of astronomical studies). The force of gravity acting on a small mass m placed on the surface of a spherical planet (that is, at a distance R from its centre) is mg, where g is its surface gravity. The attraction between the entire planet of mass M and the small mass m is described by Newton’s famous law of universal gravitation, which states that two masses M and m at distance r attract with a force of intensity

where G = 6.67 · 10⁻¹¹ N · m²/kg² is the gravitational (or Newton) constant. Newton also told us that a spherical planet behaves as if its mass were concentrated at its centre (the iron sphere theorem). Then, for a particle on the surface of a planet, we set the distance r equal to the radius of the planet R and we have

The small mass m cancels out and the value of the surface gravity is the same,

for all masses m. In other words, if no other forces (air friction, etc.) are present, all bodies (and all climbers) fall with the same acceleration independent of their mass or internal composition. This key fact, which goes against the erroneous intuition of Aristotle and of the ancient Greek philosophers (who didn’t bother experimenting), was established empirically by Galileo Galilei in 1589. It is called universality of free fall and is peculiar to gravity. None of the other three fundamental forces of nature (electromagnetic force, strong nuclear force, and weak nuclear force) share this feature. This simple fact is the basis of Einstein’s theory of General Relativity which describes gravity in modern physics⁶ [Carroll (2004); Wald (1984); Hartle (2003); Misner, Thorne, and Wheeler (1973)]. But let’s proceed with our subject. If we substitute in Eq. (1.2) the values of the mass and radius of the Earth M = 5.978 · 10²⁴ kg and R = 6370 km, we obtain the value of the acceleration of gravity g_Earth = 9.8 m/s² that we started our discussion with, and that we measure experimentally.

This is all fine for a spherical planet. However, in the space around our planet and around other Solar System planets, we see asteroids and other bodies which have irregular shape, like potatoes. We also see that larger bodies, however, assume spherical shape apart from very minor irregularities on t...

Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Dedication
• Preface
• An important note to readers
• List of Notations
• Acknowledgments
• Contents
• List of Table
• List of Figures
• 1. Mountains high or low, hard or soft
• 2. Gravity rules
• 3. Water, snow, and ice
• 4. Glacier puzzles
• 5. Heat, cold, and air
• 6. Rock climbing
• 7. Miscellaneous
• 8. Epilogue
• Appendix A
• Appendix B
• Appendix C
• Appendix D
• Bibliography
• Index