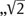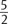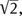Zahlen

Vojtech Kolman

• Editore: De Gruyter
• Anno: 2016
• ISBN:
  9783110480924
• Edizione: 1
• Argomento: Philosophy
• Categoria: Epistemology in Philosophy

Warum schon bei Platon die Zahlen und ihr gutes Verständnis einen speziellen Platz in der philosophischen Bildung einnehmen, ist zunächst ein Rätsel. Eine Aufhebung der zukunftsweisenden Leistungen der Pythagoräer besonders in der Harmonielehre gegenüber mystifizierendem Verständnis eines Pythagoräismus ist daher nach wie vor interessant, auch noch im Blick auf Freges 'drittes Reich' abstrakter Gegenstände oder Cantors Mengenlehre. Zahlen sind von philosophischem Interesse durch ihr enges Verhältnis zu den Formen von Rationalität und Sprache – und wegen der Möglichkeit, Aussagen nicht bloß über Zahlen selbst, sondern auch über andere Verhältnisse durch Zahlen zu kodieren und dadurch zum Thema zu machen. Auf einfach nachvollziehbare Weise wird außerdem die Verschränkung von mathematischem Fortschritt, von Problemen und ihren Aufhebungen vorgeführt oder skizziert, etwa die Entdeckung inkommensurabler Größenverhältnisse und das Rechnen mit infinitesimalen Größen, Cantors Stufen des Unendlichen, Brouwers Intuitionismus, Gödels Unvollständigkeitsätze, u.a.m. Die Philosophie der Mathematik wird zum Lehrstück logischer Selbstreflexion überhaupt.

1Grundzahlen

Das Zählen ist eine grundlegende menschliche Tätigkeit, die schon in der Rechenkunst der Babylonier und Ägypter hoch entwickelt war. Aber erst in der griechischen Mathematik ist die Zahl zu einem Gegenstand des Denkens geworden, zunächst wohl in der altpythagoräischen Lehre vom Geraden und Ungeraden, wie sie im IX. Buch von Euklids Elementen erhalten geblieben ist. In den Elementen gibt es auch eine erste explizite Definition der Zahl (arithmos):

die Zahl ist die aus Einheiten zusammengesetzte Menge.1

Aus heutiger Perspektive erscheint die Definition noch als sehr naiv oder bloß orakelhaft, zumal das begriffliche Feld der Zahlen und ihrer Familienähnlichkeiten, wie Wittgenstein solche Fälle nennt,2 sich als wesentlich komplizierter darstellen. Denn man hat heute nicht nur die Zahl im Sinne des Begriffs der natürlichen Zahlen, sondern die Zahlen im Sinne verschiedener Arten von Zahlen wie der rationalen oder reellen Zahlen oder aber auch der endlichen und unendlichen Ordinal- und Kardinalzahlen zu erläutern. Hier gibt es keine gemeinsame Definition.

Der Sache nach hatte das William James schon vor Wittgenstein und seinem Konzept eines ‚Sprachspiels‘ am Fall des Religionsbegriffes und anhand des Kontrasts zwischen der Religion und den Religionen demonstriert.3 So wie man monotheistische, polytheistische, atheistische, auch philosophische, politische, institutionelle oder rein persönliche Religionen kennt, gibt es auch eine Mannigfaltigkeit der Zahlenarten, welche keine gemeinsame Charakteristik haben. Für die Operationen, strukturellen Eigenschaften oder Anwendungsgebiete der Zahlen gibt es allerdings Ketten von partiellen Ähnlichkeiten, die etwa die natürlichen Zahlen sowohl mit den Ordinalzahlen als auch den reellen und komplexen Zahlen verbinden. Im Laufe der Zeit hat man für verschiedene Zwecke verschiedene Zahlenbereiche eingeführt, u. a. die so genannten negativen, algebraischen, imaginären, infinitesimalen, hyperkomplexen, transfiniten oder Nichtstandard-Zahlen.4 Gleichzeitig haben sich die Begriffe der natürlichen (kardinalen und ordinalen) und der reellen Zahl (des Kontinuums) weiterentwickelt. Das geschah nicht nur extensional (in gewissen Erweiterungen der natürlichen Zahlenreihe und der verschiedenen reellen Zahlenkörper), sondern auch intensional (es gibt verschiedene Konstruktionen des Kontinuums) und damit begründungstheoretisch (es gibt verschiedene Antworten auf die Frage von Richard Dedekind: „Was sind und was sollen die Zahlen?“).

Ohne nach einer allgemeingültigen Definition zu streben, was in Hinblick auf die Mannigfaltigkeit der Zahlengebiete offenbar aussichtslos ist, kann man den Zahlbegriff mit dem verwandten Allgemeinbegriff des Quantums verbinden, der Menge, Größe und Zahl umfasst. Die allgemeine Aufgabe der Zahlen kann dann als Quantifizierung angesehen werden. Dabei fällt auch schon der Zusammenhang von Zählen und Sprechen auf, wenn wir Ausdrücke wie „erzählen“ oder „to give an account“ betrachten. Diese Verknüpfung ist am Ende auch für den Übergang von Zahlen als Momenten (Hilfsmittel) einer Praxis des Zählens, Rechnens und Messens zu den Zahlen als selbständigen (d. h. rein quantitativ unterschiedenen) Objekten der Untersuchung verantwortlich, welche je eigene Eigenschaften und eigene Urteilsformen haben.

1.1Von der synkategorematischen zur objektiven Rede

Mit Frege gesehen, also sprachanalytisch, handelt es sich beim Übergang von den so genannten (empirisch) benannten Zahlen bzw. der entsprechenden Ausdrucksformen, wie „5 Äpfel“, „2,5 Pfund“ oder vielleicht sogar schon

Fuß“, zu den reinen Zahlen, wie 5,

und

die eine selbständige Bedeutung haben, um eine gegenstandsbildende Abstraktion. Es geht um den Übergang von Sätzen wie

(a)im Korb gibt es 5 Äpfel

zu Sätzen wie

(b)5 ist eine Primzahl.

Nach Freges bekannter Analyse5 findet man den Zusammenhang in der Beobachtung, dass im praktischen Zählen der beigefügte Begriff ‚Apfel‘ oder ‚Korb‘ die relevante Einheit (also 1 Apfel, 1 Korb) nennt, ohne welche die zu einer Zahlangabe führende Frage „wie viel?“ gar keinen konkreten Sinn hat. Im Unterschied dazu erhält man durch die Frage

(c)wie viele Äpfel gibt es im Korb?

eine klare Anleitung, wie der Ausdruck

(d)die Anzahl der Äpfel im Korb

zu verstehen ist, auch wenn (c) zunächst vielleicht nur mit Hilfe einer Redewendung wie der folgenden zu beantworten ist:

(e)die Anzahl der Äpfel in dem Korb ist gleich der Anzahl der Knöpfe in der Tasche.

In (e) unterstellt man noch keinen eigenständigen Gegenstandsbereich der (An-) Zahlen, sondern nur die Praxis einer umkehrbar eindeutigen, oder bijektiven Zuordnung der unter die entsprechenden Begriffe fallenden Gegenstände. Unter Bijektion versteht man dabei weiterhin eine Zuordnung, welche jedem Gegenstande vom Typ A (Apfel) genau einen Gegenstand vom Typ B (Knopf) beiordnet, so dass am Ende die Gegenstände A mit den Gegenständen B und umgekehrt B mit A eindeutig verpaart sind und keine nichtverpaarten Gegenstände verbleiben. (Siehe Kap. 8 für eine weitere Erklärung.) Es ist genau diese Praxis einer bijektiven Zuordnung, welche für die Einführung der natürlichen Zahlen in die Gemeinsprache verantwortlich ist.

Die Erfindung der Zahlen wird daher auf interessante Weise zu einem paradigmatischen Analogon für die Erfindung des Geldes. Die Abstraktion des reinen Geldwerts ist ja in der Tat ein Motor der natürlichen Erweiterung des Tauschhandels. Auch das Geld hat eine Bedeutung nur im Ganzen des gemeinsamen menschlichen Handelns. Es gehört nie zu den Endzielen, sondern immer nur zu den Ziele vermittelnden Instrumenten. Dass manche das ganze Leben der Mathematik, dem Bankwesen, dem Studium der Sprache(n), oder der rein Geizige ausschließlich der Vermehrung des Geldbesitzes, weihen können, ist eine andere Sache, die mit der selbst-bewussten, selbst-reflexiven Natur des Menschen und der Möglichkeit der Arbeitsteilung und Themenfokussierung zusammenhängt. Für die arithmetische Sprache werden wir besonders in Kap. 11 auf diesen Kontext zurückkommen.

Die Rolle der Antwort (e) in der Formation einer wissenschaftlichen Arithmetik ist dabei eine dreifache. (1) Erstens markiert sie einen Übergang zu der verwandten Antwort

(f)die Anzahl der Äpfel in dem Korb ist 5,

in welcher man die Präsenz einer konkreten Tasche als Behälter konkreter Knöpfe ersetzt durch die situationsinvariante Möglichkeit, eine Anzahl durch ein Zahlwort zu kennzeichnen, welches die Anzahl der Vorgängerzahlwörter zählt. Da die sprachlichen und kulturellen Besonderheiten der Artikulation der Zahlterme etwa im griechischen, römischen oder arabischen System gleichgültig sind, sagen wir, dass wir nicht die Zahlwörter, sondern die abstrakten Zahlen zum Zählen verwenden. Man ersetzt so die Menge der konkreten Knöpfe durch abstrakte Einheiten, die es sozusagen in jedermanns ‚Kopf‘ gibt. (2) In (e) und (f) zeigt sich zweitens, dass die Auffassung der natürlichen Zahlen als endliche Kardinal- bzw. Ordinalzahlen, wie sie sich in Antworten auf die Grundfragen „wie viel?“ bzw. „an der wievielten Position in einer Reihe?“ manifestiert, von Anfang an eng zusammenhängen. Schon aus mnemotechnischen Gründen kann man nämlich die zu zählenden Einheiten mit ihrer Ordnung in der entstehenden Reihe gleichsetzen und beides dann als 1, 2, 3, 4, … notieren, d. h. in der Form einer Folge, deren Glieder nicht nur die Stellung, sondern auch die Anzahl der vorangehenden Glieder (einschließlich des betreffenden Gliedes selbst oder der noch einzuführenden Null) vertreten. (3) Drittens demonstrieren die Antworten (e) und (f) schon ihrer Form nach eine äußerst wichtige logische Einsicht, welche (u. a.) Frege in seinen Grundlagen explizit machte,6 nämlich dass die Erweiterung der bestehenden Redepraxis um die neuen Sprachmittel wie „Anzahl“ oder „5“ mit dem Phänomen der Gleichheit zusammenhängt.

1.2Die Gleichheit und ihre Logik

Wie schon David Hume in seinen erkenntnistheoretischen Untersuchungen gezeigt hatte,7 ist die Identität und die Permanenz der Gegenstände der Außenwelt (genauso wie die Identität von ‚Ich‘ und die Kausalität der Ereignisse) nicht einfach aus den Sinneseindrücken herzuleiten. Denn die Sinne geben uns immer nur eine Abfolge von stets verschiedenen und sogar partiell unabhängigen, auch perspektivisch kontingenten ‚Empfindungen‘, die als solche noch keine Wahrnehmungen von Gegenständen sind. Rein empirisch ist also, wie es scheint, ein Satz der Form

M und N sind gleich

immer ‚falsch‘ oder bestenfalls ‚approximativ wahr‘. Humes ‚skeptische Lösung‘ des Paradoxes, dass wir trotzdem an die von uns unabhängige (und kausal gegliederte) Welt der Gegenstände glauben, welche in ihrer Identität hinter der Diversität der Erscheinungen stehen, besagt bekanntlich, es gebe dafür keine ‚rationalen‘ Gründe (im Sinn theoretischen Wissens), sondern nur praktische Opportunitäten, auf der Grundlage einer sich auf gewisse Relationen von Ähnlichkeit und Regelmäßigkeit stützenden Gewöhnung. Doch Gewöhnung ist etwas, was in uns und nicht in der Außenwelt wurzelt. Daher ist bei Hume in gewissem Sinne schon die Reaktion Kants vorweggenommen, welcher die passive Macht der Gewohnheit zumindest partiell durch die Spontaneität tätigen Handelns und damit auch einer Art gesetzgebender Vernunft mit ihren vereinheitlichenden Funktionen zu ersetzen suchte.

Die allgemeine Rolle der Gleichheit in der ganzen Geschichte besteht nun darin, dass sie nichts unmittelbar Gegebenes (Humes ‚impression‘, dann auch ‚perception‘ und die davon abgeleitete ‚idea‘) darstellt, sondern als eine (vermittelte) Verneinung der (unmittelbaren) Ungleichheit zu deuten ist. Die unmit...

Indice dei contenuti

• Cover
• Titelseite
• Impressum
• Inhaltsverzeichnis
• Einleitung
• 1 Grundzahlen
• 2 Proportionen
• 3 Inkommensurabilität
• 4 Algebraische Zahlen
• 5 Infinitesimale Größen
• 6 Der Funktionsbegriff
• 7 Diagonalisierung
• 8 Transfinites
• 9 Logizismus
• 10 Wahlfolgen
• 11 Axiomatizismus
• Schluss
• Anmerkungen
• Literatur
• Namenregister
• Sachregister